
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И фазы вынужденных колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как видно из (5.42), амплитуда вынужденных колебаний зависит от частоты и при некоторой частоте достигает максимума. Эта частота называется резонансной Максимуму амплитуды соответствует минимум знаменателя (5.40), поэтому производная от выражения в знаменателе (5.40) должна быть равна нулю:
Уравнение (5.43) имеет три решения:
Подставив это значение частоты в выражение в (5.40), найдем значение амплитуды при резонансе:
Зависимость амплитуды колебаний от частоты внешнего воздействия называют резонансной кривой или резонансной характеристикой. Примерный вид резонансных характеристик колебательной системы, в которой изменяют затухание, показан на рисунке 5.8. Если в системе отсутствует затухание, т.е. коэффициент затухания С увеличением затухания резонансная амплитуда уменьшается, резонансная частота в соответствии с (5.43) также уменьшается. Поэтому максимум резонансной кривой становится ниже и смещается влево (кривые 2, 3, 4). Резонансные характеристики несимметричны: если частота вынуждающей силы стремится к нулю, то все резонансные кривые стремятся к одинаковому значению Зависимость сдвига фаз
Лекция № 6. ЭЛНЕМЕНТЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ ПОСТУЛАТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. Для описания движения тел со скоростями, сравнимыми со скоростью света в пустоте – с –Эйнштейном была разработана релятивистская механика, которая учитывает требования созданной им специальной теории относительности. В основе этой теории лежат два постулата. Принцип относительности Эйнштейна является распространением механического принципа относительности Галилея на все физические явления и утверждает, что все законы природы одинаковы во всех инерциальных системах отчета. Неизменность вида уравнений при замене в них координат и времени одной инерциальной системы отсчета соответствующими величинами другой, называется инвариантностью уравнений. Поэтому принцип относительности Эйнштейна следует формулировать следующим образом: уравнения законов природы инвариантны по отношению к преобразованиям координат и времени от одной инерциальной системы отчета к другой. Принцип постоянства скорости света утверждает, что скорость света в пустоте одинакова во всех инерциальных системах отчета и не зависит от движения источников приемников света.
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Из преобразований Галилея следует закон сложения скоростей, согласно которому Формулы преобразований координат, согласующиеся с принципом постоянства скорости света, нашел Лоренц. Эти формулы называются преобразованиями Лоренца и имеют вид:
Часто встречающееся отношение
Обратный переход к координатам системы
Необходимо подчеркнуть две особенности формул преобразований Лоренца. С одной стороны, пространственные координаты и время оказываются взаимосвязанными и рассматриваются в теории относительности как единое четырехмерное пространство-время. С другой стороны, формулы преобразований Лоренца теряют смысл, если
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 764; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.207 (0.006 с.) |

 , а само явление резонансом.
, а само явление резонансом.
 . (5.43)
. (5.43) ,
,  . Нулевое и отрицательное значение
. Нулевое и отрицательное значение  не имеют физического смысла, а значит резонансная частота
не имеют физического смысла, а значит резонансная частота . (5.44)
. (5.44) . (5.45)
. (5.45) , то резонансная амплитуда
, то резонансная амплитуда  , а
, а  . На рисунке этому условию соответствует кривая 1. Практически такая ситуация не реализуется, но чем меньше затухание, тем ближе резонансная кривая к этому идеальному случаю.
. На рисунке этому условию соответствует кривая 1. Практически такая ситуация не реализуется, но чем меньше затухание, тем ближе резонансная кривая к этому идеальному случаю. , соответствующему смещению системы из положения равновесия под действием постоянной силы. При возрастании частоты вынуждающей силы все резонансные кривые стремятся к нулю. Это означает, что под действием быстропеременной силы система не успевает заметно сместиться из положения равновесия и амплитуда колебаний становится незначительной. (Вспомните раскачивание качелей… Приложив постоянную силу определенной величины, мы получим некоторое смещение из положения равновесия. Если с такой же по амплитуде силой пытаться раскачивать качели на максимально доступной частоте – отклонение от положения равновесия будет совсем незначительным.)
, соответствующему смещению системы из положения равновесия под действием постоянной силы. При возрастании частоты вынуждающей силы все резонансные кривые стремятся к нулю. Это означает, что под действием быстропеременной силы система не успевает заметно сместиться из положения равновесия и амплитуда колебаний становится незначительной. (Вспомните раскачивание качелей… Приложив постоянную силу определенной величины, мы получим некоторое смещение из положения равновесия. Если с такой же по амплитуде силой пытаться раскачивать качели на максимально доступной частоте – отклонение от положения равновесия будет совсем незначительным.) между периодическим внешним воздействием и колебаниями, совершаемыми системой, называют фазовой характеристикой системы.
между периодическим внешним воздействием и колебаниями, совершаемыми системой, называют фазовой характеристикой системы. Вынужденные колебания отстают по фазе от вынуждающей силы. Примерный вид этой зависимости показан рисунке 5.8. Отметим, что независимо от затухания в системе сдвиг по фазе достигает значение
Вынужденные колебания отстают по фазе от вынуждающей силы. Примерный вид этой зависимости показан рисунке 5.8. Отметим, что независимо от затухания в системе сдвиг по фазе достигает значение  при частоте, равной собственной част оте колебаний системы. Следовательно, эта зависимость может быть использована для определения
при частоте, равной собственной част оте колебаний системы. Следовательно, эта зависимость может быть использована для определения  .
. Вернемся к рассмотрению двух инерциальных систем отчета
Вернемся к рассмотрению двух инерциальных систем отчета  и
и  , которые мы ввели при рассмотрении преобразований Галилея. Напомним, что оси
, которые мы ввели при рассмотрении преобразований Галилея. Напомним, что оси  и
и  системы
системы  и
и  и
и  совпадают по направлению, система
совпадают по направлению, система  , направленной вдоль оси
, направленной вдоль оси  . Применим этот закон к распространению света. Если в системе
. Применим этот закон к распространению света. Если в системе  . Но это противоречит принципу постоянства скорости света с. Следовательно, преобразования Галилея должны быть заменены другими формулами.
. Но это противоречит принципу постоянства скорости света с. Следовательно, преобразования Галилея должны быть заменены другими формулами. ;
;  ;
;  ;
;  . (6.1)
. (6.1) бывает удобно заманить общепринятым обозначением
бывает удобно заманить общепринятым обозначением  . В этом случае преобразования Лоренца (6.1) приобретают вид:
. В этом случае преобразования Лоренца (6.1) приобретают вид: ;
; 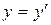 ;
;  ;
;  (6.2)
(6.2) ;;
;;  ;
;  (6.3)
(6.3) . Эта ихособенность математически отражает тот факт, что скорость движения света в пустоте является предельной скоростью распространения взаимодействий в пространстве. Со скоростью света могут двигаться только особые частицы, такие, как фотоны, обладающие нулевой массой покоя. Для обычных, окружающих нас тел, движение со скоростью
. Эта ихособенность математически отражает тот факт, что скорость движения света в пустоте является предельной скоростью распространения взаимодействий в пространстве. Со скоростью света могут двигаться только особые частицы, такие, как фотоны, обладающие нулевой массой покоя. Для обычных, окружающих нас тел, движение со скоростью  невозможно.
невозможно.


