
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия. Закон сохранения энергииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Энергия – это скалярная физическая величина, являющаяся универсальной мерой различных форм движения и взаимодействия тел. Количественной характеристикой процесса обмена энергией между взаимодействующими телами является работа. Элементарная работа силы
где α – угол между векторами
Работа силы на участке траектории 1-2:
Кинетическая энергия механической системы – это энергия механического движения этой системы:
Приращение кинетической энергии частицы на элементарном перемещении равно элементарной работе на том же перемещении: Потенциальная энергия механической системы определяется взаимным расположением тел системы и характером сил взаимодействия между ними. Силы, работа которых не зависит от формы траектории тела, а определяется лишь начальным и конечным положением тела, называются консервативными. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
а при конечном изменении:
Связь между консервативной силой и потенциальной энергией:
где градиент потенциальной энергии равен: Примерами консервативных сил являются силы тяготения, тяжести, упругости. Потенциальная энергия частицы, находящейся в поле силы тяжести равна:
где h отсчитывается от произвольного уровня. Потенциальная энергия упругодеформированного тела:
где k – коэффициент упругости, х – абсолютная деформация. Полная энергия механической системы равна сумме кинетической и потенциальной энергии:
Закон сохранения механической энергии: полная механическая энергия системы тел, находящихся под действием только консервативных сил, остается постоянной:
где
Если система замкнута и силы взаимодействия между частицами консервативны, то полная энергия содержит лишь два слагаемых: При наличии неконсервативных сил полная механическая энергия системы не сохраняется:
где Неконсервативными, в частности, являются силы трения и силы сопротивления среды. Работа этих сил, как правило, отрицательна. Поэтому при наличии этих сил полная механическая энергия системы уменьшается, переходя во внутреннюю энергию тел, что приводит к их нагреванию. Такой процесс называется диссипацией. Силы, приводящие к диссипации энергии, называются диссипативными. Закон сохранения энергии имеет всеобщий характер. Он применим ко всем без исключения процессам, происходящим в природе. Полное количество энергии в изолированной системе тел и полей всегда остается постоянным; энергия лишь может переходить из одной формы в другую. Этот факт является проявлением неучтожимости материи и ее движения.
Движение тела, соскальзывающего По наклонной плоскости
Рассмотрим движение бруска вдоль наклонной плоскости. На него действуют: сила тяжести
Уравнение движения бруска по второму закону Ньютона имеет вид:
или в скалярной форме в проекциях на оси х и у:
Отсюда ускорение бруска с учетом формулы (1.2) равно:
а сила трения
Брусок начинает движение без начальной скорости с ускорением
Отсюда
Применим закон сохранения энергии к движению бруска по наклонной плоскости. Так как на брусок действует сила трения, то рассматриваемую механическую систему следует считать неконсервативной. Поэтому изменение полной механической энергии бруска при его движении по наклонной плоскости равно работе силы трения:
Полная энергия бруска на вершине наклонной плоскости равна потенциальной энергии, так как начальная скорость бруска равна нулю: Полная энергия бруска у основания наклонной плоскости равна кинетической энергии:
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 904; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.200.21 (0.012 с.) |

 на бесконечно малом перемещении
на бесконечно малом перемещении  равна скалярному произведению векторов
равна скалярному произведению векторов  :
: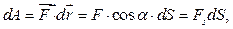
 - элементарный путь;
- элементарный путь;  - проекция вектора
- проекция вектора  Рис. 1.4
Рис. 1.4

 .
. а при конечном перемещении из точки 1 в точку 2:
а при конечном перемещении из точки 1 в точку 2: 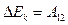 , т.е. приращение кинетической энергии частицы на некотором перемещении равно алгебраической сумме работ всех сил, действующих на частицу на том же перемещении.
, т.е. приращение кинетической энергии частицы на некотором перемещении равно алгебраической сумме работ всех сил, действующих на частицу на том же перемещении. ,
, .
. ,
, (
(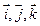 – единичные векторы координатных осей).
– единичные векторы координатных осей). ,
, ,
,
 ,
, – потенциальная энергия системы во внешнем силовом поле;
– потенциальная энергия системы во внешнем силовом поле;  – взаимная потенциальная энергия частиц системы.
– взаимная потенциальная энергия частиц системы. . В этом случае закон сохранения механической энергии гласит: полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной.
. В этом случае закон сохранения механической энергии гласит: полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной. ,
, – работа неконсервативных сил.
– работа неконсервативных сил. , направленная вертикально вниз; сила нормальной реакции опоры
, направленная вертикально вниз; сила нормальной реакции опоры 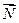 , направленная перпендикулярно к плоскости, и сила трения
, направленная перпендикулярно к плоскости, и сила трения 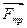 , направленная противоположно движению бруска вдоль плоскости (рис. 1.3).
, направленная противоположно движению бруска вдоль плоскости (рис. 1.3). Рис.1.3
Рис.1.3

 .
. (1.4)
(1.4)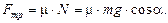 (1.5)
(1.5) и проходит за время
и проходит за время 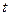 расстояние
расстояние 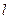 , равное длине наклонной плоскости, следовательно:
, равное длине наклонной плоскости, следовательно: , (1.6)
, (1.6) . (1.7)
. (1.7) . (1.8)
. (1.8) .
. . Подставим это в закон сохранения энергии (1.8):
. Подставим это в закон сохранения энергии (1.8): или
или 
 . (1.9)
. (1.9)


