
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энтальпия . Закон Гесса. Термохимические уравнения.Содержание книги
Поиск на нашем сайте
Энтальпия. Закон Гесса. Термохимические уравнения. Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц. Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении. Закон Гесса. В 1841 году российский ученый Г.И.Гесс открыл закон, получивший его имя. Тепловой эффект реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, т.е. от числа и характера промежуточных стадий. Закон Гесса лежит в основе термохимических расчетов. Однако рамки его действия ограничены изобарно-изотермическими и изохорно-изотермическими процессами. Проиллюстрируем закон Гесса на примере реакции сгорания метана:СН4 + 2О2 = СО2 + 2Н2О (г),dH = - 802,34 кДж.Эту же реакцию можно провести через стадию образования СО:СН4 +3/2О2 = СО + 2Н2О (г), dH°2 = - 519,33 кДж, СО + 1/2O2 = СО2,dH°з = - 283,01 кДж,dH=dH1 + dH°3 = (- 519,33) кДж + (- 283,01) кДж = - 802,34 кДж. - тепловой эффект реакции, протекающей по двум путям, одинаков. Так как энтальпия зависит от со стояния системы, но не зависит от пути процесса, то, если при проведении процесса система вернулась в исходное состояние, суммарное изменение энтропии системы равно нулю (dH = 0). Процессы, в которых система после последовательных превращений возвращается в исходное состояние, называются круговыми процессами или циклами. Итак, закон Гесса показывает, что каким бы путем не протекала реакция, ее тепловой эффект будет одинаков, если при этом не меняется конечное и исходное состояния системы. Энтальпия химических реакций. Закон Гесса позволяет рассчитать энтальпию химических реакций. Согласно следствию из закона Гесса, энтальпия химической реакции равна сумме энтальпии образования продуктов реакций за вычетом суммы энтальпий образования веществ исходных с учетом стехиометрических коэффициентов Стандартный тепловой эффект реакции получения водорода из природного газа: СН4 + 2Н2О(г) = СО2 + 4Н2 определяется по уравнению: ∆H0298 =∆Hco2 298 +4∆HH2 - ∆HCH4 -2∆HH2O Подставляя значения величин энтальпий образования из приложения 2 (в кДж/моль), получаем dH°298 = -1-393,510-1(-74,85)-2(241,82) = +164,98 кДж/моль. Как видно, данная реакция является эндотермической. Термохимические уравнения. Теплота, высвобождаемая или поглощаемая конкретной химической реакцией, пропорциональна степени превращения реагентов, определяемой по количеству любого из расходуемых либо образующихся продуктов. Изменение внутренней энергии или энтальпии реагирующей системы определяют по химическому уравнению реакции. Например, сгорание смеси газообразных метана и кислорода описывается термохимическим уравнением
7. Стандартные теплоты образования и сгорания. Термохимические расчеты и их использование для энергетической характеристики биохимических процессов Стандартная теплота образования. Из закона сохранения энергии следует, что, когда вещество образуется из атомов и (или) более простых веществ, внутренняя энергия или энтальпия системы меняется на определенную величину, называемую теплотой образования данного вещества. Теплота образования может быть определена различными способами, в том числе прямыми калориметрическими измерениями и путем косвенного расчета (на основе закона Гесса) из теплоты реакции, в которой участвует данное вещество. При проведении расчетов пользуются стандартными (при p = 1 атм и T = 298 K) теплотами образования веществ, входящих в уравнение реакции. Например, стандартную теплоту (энтальпию) образования метана можно вычислить с помощью термохимического уравнения
Хотя эта реакция практически неосуществима при 25 С, стандартная теплота образования метана косвенно рассчитывается по измеренным теплотам сгорания метана, водорода и графита. На основе закона Гесса устанавливается, что теплота реакции равна разности между теплотами сгорания веществ, указанных в левой части уравнения, и теплотами сгорания веществ, указанных в правой части уравнения реакции (взятых с соответствующими знаками и стехиометрическими коэффициентами). Помимо использования термохимических данных для решения проблем практического использования тепловой энергии, они широко применяются при теоретической оценке энергий химических связей. Тепловой эффект реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции. Закон лежит в основе термохимических расчетов. Рассмотрим реакцию сгорания метана: Эту же реакцию можно провести через стадию образования СО: Итак, видно, тепловой эффект реакции, протекающей по двум путям, одинаков. При термохимических расчетах для определения тепловых эффектов применяют следствия из закона Гесса. 8. Второе начало термодинамики. Энтропия. Состояние некоторого количества вещества можно охарактеризовать, указав, например, температуру, давление – это характеристики макросостояния или указать мгновенные характеристики каждой частицы вещества – ее положение в пространстве (x i, y i, z i) и скорости перемещения по всем направлениям (v x, v y, v z) – это характеристики микросостояния вещества. Так как вещество состоит из огромного числа частиц, то данному макросостоянию отвечает огромное число микросостояний. Число микросостояний, которое соответствует данному макросостоянию вещества, называется термодинамической вероятностью состояния системы – W. Величина W есть число различных способов, посредством которых реализуется данное состояние вещества. Макросостояние тем вероятнее, чем большим числом микросостояний оно осуществляется. Так для системы из 10 молекул W близко к 10000. Оказалось удобнее и проще характеризовать состояние системы не самой вероятностью осуществления данного макросостояния, а величиной, пропорциональной ее логарифму. Эта величина называется энтропией и обозначается буквой S. Как показано Больцманом, · S – характеризует состояния системы и возможные изменения состояний, поэтому является функцией термодинамического состояния. Каждому состоянию системы соответствует определенное значение энтропии. Следовательно, вероятность различных состояний системы (газовое, жидкое, твердое) можно количественно выразить значением энтропии. Абсолютные значения энтропии можно определить экспериментально для простых и сложных веществ или взять из справочника термодинамических величин. Величину S можно рассматривать как меру неупорядоченности состояния системы, то есть как количественную меру беспорядка. 2 закон термодинамики В изолированных системах самопроизвольно протекают только те процессы, которые сопровождаются ростом энтропии системы. В справочниках приводится, так называемая, стандартная энтропия b B + d D = l L + m M изменение энтропии (энтропия реакции) можно рассчитать как разницу между суммарной энтропией продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов в соответствии с уравнением где n j, m i – коэффициенты уравнения реакции для продуктов и исходных веществ; Энтропия растет (Δ S > 0) в процессах, связанных с повышением температуры, при плавлении вещества, при испарении, при расширении системы, растворении. В этих случаях увеличение числа частиц и энергии теплового движения увеличивает беспорядок и, следовательно, увеличивается энтропия, и наоборот – охлаждение, конденсация, кристаллизация, реакции с уменьшением объема – сопровождаются уменьшением энтропии (Δ S < 0). "Носителями" энтропии являются газы, обладающие высокими значениям. 9.Стандартные энтропии. Энергия Гиббса. Если процесс протекает самопроизвольно, то внутренняя энергия (энтальпия) должны уменьшаться, а энтропия увеличиваться. Для сравнения этих величин их надо выразить в одних единицах, а для этого Δ S умножить на T. В этом случае имеем Δ Н – энтальпийный фактор и Т Δ S -энтропийный фактор. В ходе реакции частицы стремятся к объединению, что ведет к уменьшению энтальпии (Δ Н < 0), с другой стороны – должна возрастать энтропия, т.е. увеличиваться число частиц в системе (Т Δ S > 0). "Движущая сила" реакции определяется разностью между этими величинами и обозначается Δ G. Δ G p,T = Δ H – T Δ S и называется изменением энергии Гиббса (изобарно-изотермический потенциал). Энергия Гиббса - это часть энергетического эффекта реакции, которую можно превратить в работу, поэтому ее называют свободной энергией. Это тоже термодинамическая функция состояния и, следовательно, для реакции b B + d D = l L + m M, энергию Гиббса химической реакции можно рассчитать как сумму энергий Гиббса образования продуктов реакции за вычетом энергий Гиббса образования исходных веществ с учетом стехиометрических коэффициентов по формуле: Δ G = l Δf G L + m Δf G M – d Δf G D – b Δf G B. где Δf G – энергия Гиббса образования веществ. Энергия Гиббса образования веществ это изменение энергии Гиббса системы при образовании 1 моль вещества из простых веществ, устойчивых при 298 К. Энергия Гиббса образования простых веществ Δf G принимается равной нулю. Если образующееся вещество и исходные простые вещества находятся в стандартных состояниях, то энергия Гиббса образования называется стандартной энергией Гиббса образования вещества Δf G 0. Ее значения приводятся в справочниках. Полученное значение Δ G является критерием самопроизвольного течения реакции в прямом направлении, если Δ G < 0. Химическая реакция не может протекать самопроизвольно в прямом направлении, если энергия Гиббса системы возрастает, т.е. Δ G > 0. Если Δ G = 0, то реакция может протекать как в прямом, так и в обратном направлениях, т.е. реакция обратима. Направление химических реакций зависит от их характера. Так, условие Δ G < 0 соблюдается при любой температуре для экзотермических реакций (Δ Н < 0), у которых в ходе реакции возрастает число молей газообразных веществ, и, следовательно, энтропия (Δ S > 0). У таких реакций обе движущие силы (Δ Н) и (Т Δ S) направлены в сторону протекания прямой реакции и Δ G < 0 при любых температурах. Такие реакции являются необратимыми. Свойства воды. Уникальные свойства воды определяются структурой ее молекулы. Молекула воды состоит из атома О, связанного с двумя атомами Н полярными ковалентными связями. Характерное расположение электронов в молекуле воды придает ей электрическую асимметрию. Более электроотрицательный атом кислорода притягивает электроны атомов водорода сильнее, в результате общие пары электронов смещены в молекуле воды в его сторону. Основные понятия: растворимость, растворитель, растворенное вещество. Классификация растворов (по содержанию растворенного вещества, по агрегатному состоянию). Насыщенный раствор – термодинамически устойчивая равновесная система, в которой скорость растворения вещества равна скорости выделения его из раствора. Ненасыщенный раствор – термодинамически устойчивая неравновесная система, в которой концентрация вещества меньше, чем в насыщенном растворе, и поэтому скорость растворения больше скорость выделения. Пересыщенный раствор – термодинамически неустойчивая псевдоравновесная система, в которой концентрация вещества больше, чем в насыщенном растворе, и поэтому скорость выделения больше скорости растворения. Концентрированный раствор – раствор с высоким содержанием растворенного вещества. Разбавленный – с низким содержанием растворенного вещества. Гомогенные растворы – истинные растворы. Гетерогенные растворы – коллоидные растворы Гомогенные и гетерогенные растворы. Гомогенные растворы – истинные растворы. Гетерогенные растворы – коллоидные растворы Коэффициент растворимости. Коэффициент растворимости – характеристика раствора, означающая число единиц массы безводного вещества, насыщающего при данных условиях 100 единиц массы растворителя. Измеряется в m (г) вещества на 100 г растворителя. Закон эквивалентов. Химические элементы соединяются друг с другом в строго определенных количествах, соответствующих их эквивалентам. Понятие эквивалента было введено для сопоставления соединительной способности разных элементов. Эквивалентом химического элемента называют такую его массу, которая соединяется с 1,008 ч. м. (части массы) водорода или 8 ч. м. кислорода или замещает эти массы в соединениях.
Энтальпия. Закон Гесса. Термохимические уравнения. Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц. Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении. Закон Гесса. В 1841 году российский ученый Г.И.Гесс открыл закон, получивший его имя. Тепловой эффект реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, т.е. от числа и характера промежуточных стадий. Закон Гесса лежит в основе термохимических расчетов. Однако рамки его действия ограничены изобарно-изотермическими и изохорно-изотермическими процессами. Проиллюстрируем закон Гесса на примере реакции сгорания метана:СН4 + 2О2 = СО2 + 2Н2О (г),dH = - 802,34 кДж.Эту же реакцию можно провести через стадию образования СО:СН4 +3/2О2 = СО + 2Н2О (г), dH°2 = - 519,33 кДж, СО + 1/2O2 = СО2,dH°з = - 283,01 кДж,dH=dH1 + dH°3 = (- 519,33) кДж + (- 283,01) кДж = - 802,34 кДж. - тепловой эффект реакции, протекающей по двум путям, одинаков. Так как энтальпия зависит от со стояния системы, но не зависит от пути процесса, то, если при проведении процесса система вернулась в исходное состояние, суммарное изменение энтропии системы равно нулю (dH = 0). Процессы, в которых система после последовательных превращений возвращается в исходное состояние, называются круговыми процессами или циклами. Итак, закон Гесса показывает, что каким бы путем не протекала реакция, ее тепловой эффект будет одинаков, если при этом не меняется конечное и исходное состояния системы. Энтальпия химических реакций. Закон Гесса позволяет рассчитать энтальпию химических реакций. Согласно следствию из закона Гесса, энтальпия химической реакции равна сумме энтальпии образования продуктов реакций за вычетом суммы энтальпий образования веществ исходных с учетом стехиометрических коэффициентов Стандартный тепловой эффект реакции получения водорода из природного газа: СН4 + 2Н2О(г) = СО2 + 4Н2 определяется по уравнению: ∆H0298 =∆Hco2 298 +4∆HH2 - ∆HCH4 -2∆HH2O Подставляя значения величин энтальпий образования из приложения 2 (в кДж/моль), получаем dH°298 = -1-393,510-1(-74,85)-2(241,82) = +164,98 кДж/моль. Как видно, данная реакция является эндотермической. Термохимические уравнения. Теплота, высвобождаемая или поглощаемая конкретной химической реакцией, пропорциональна степени превращения реагентов, определяемой по количеству любого из расходуемых либо образующихся продуктов. Изменение внутренней энергии или энтальпии реагирующей системы определяют по химическому уравнению реакции. Например, сгорание смеси газообразных метана и кислорода описывается термохимическим уравнением
7. Стандартные теплоты образования и сгорания. Термохимические расчеты и их использование для энергетической характеристики биохимических процессов Стандартная теплота образования. Из закона сохранения энергии следует, что, когда вещество образуется из атомов и (или) более простых веществ, внутренняя энергия или энтальпия системы меняется на определенную величину, называемую теплотой образования данного вещества. Теплота образования может быть определена различными способами, в том числе прямыми калориметрическими измерениями и путем косвенного расчета (на основе закона Гесса) из теплоты реакции, в которой участвует данное вещество. При проведении расчетов пользуются стандартными (при p = 1 атм и T = 298 K) теплотами образования веществ, входящих в уравнение реакции. Например, стандартную теплоту (энтальпию) образования метана можно вычислить с помощью термохимического уравнения
Хотя эта реакция практически неосуществима при 25 С, стандартная теплота образования метана косвенно рассчитывается по измеренным теплотам сгорания метана, водорода и графита. На основе закона Гесса устанавливается, что теплота реакции равна разности между теплотами сгорания веществ, указанных в левой части уравнения, и теплотами сгорания веществ, указанных в правой части уравнения реакции (взятых с соответствующими знаками и стехиометрическими коэффициентами). Помимо использования термохимических данных для решения проблем практического использования тепловой энергии, они широко применяются при теоретической оценке энергий химических связей. Тепловой эффект реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции. Закон лежит в основе термохимических расчетов. Рассмотрим реакцию сгорания метана: Эту же реакцию можно провести через стадию образования СО: Итак, видно, тепловой эффект реакции, протекающей по двум путям, одинаков. При термохимических расчетах для определения тепловых эффектов применяют следствия из закона Гесса. 8. Второе начало термодинамики. Энтропия. Состояние некоторого количества вещества можно охарактеризовать, указав, например, температуру, давление – это характеристики макросостояния или указать мгновенные характеристики каждой частицы вещества – ее положение в пространстве (x i, y i, z i) и скорости перемещения по всем направлениям (v x, v y, v z) – это характеристики микросостояния вещества. Так как вещество состоит из огромного числа частиц, то данному макросостоянию отвечает огромное число микросостояний. Число микросостояний, которое соответствует данному макросостоянию вещества, называется термодинамической вероятностью состояния системы – W. Величина W есть число различных способов, посредством которых реализуется данное состояние вещества. Макросостояние тем вероятнее, чем большим числом микросостояний оно осуществляется. Так для системы из 10 молекул W близко к 10000. Оказалось удобнее и проще характеризовать состояние системы не самой вероятностью осуществления данного макросостояния, а величиной, пропорциональной ее логарифму. Эта величина называется энтропией и обозначается буквой S. Как показано Больцманом, · S – характеризует состояния системы и возможные изменения состояний, поэтому является функцией термодинамического состояния. Каждому состоянию системы соответствует определенное значение энтропии. Следовательно, вероятность различных состояний системы (газовое, жидкое, твердое) можно количественно выразить значением энтропии. Абсолютные значения энтропии можно определить экспериментально для простых и сложных веществ или взять из справочника термодинамических величин. Величину S можно рассматривать как меру неупорядоченности состояния системы, то есть как количественную меру беспорядка. 2 закон термодинамики В изолированных системах самопроизвольно протекают только те процессы, которые сопровождаются ростом энтропии системы. В справочниках приводится, так называемая, стандартная энтропия b B + d D = l L + m M изменение энтропии (энтропия реакции) можно рассчитать как разницу между суммарной энтропией продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов в соответствии с уравнением где n j, m i – коэффициенты уравнения реакции для продуктов и исходных веществ; Энтропия растет (Δ S > 0) в процессах, связанных с повышением температуры, при плавлении вещества, при испарении, при расширении системы, растворении. В этих случаях увеличение числа частиц и энергии теплового движения увеличивает беспорядок и, следовательно, увеличивается энтропия, и наоборот – охлаждение, конденсация, кристаллизация, реакции с уменьшением объема – сопровождаются уменьшением энтропии (Δ S < 0). "Носителями" энтропии являются газы, обладающие высокими значениям. 9.Стандартные энтропии. Энергия Гиббса. Если процесс протекает самопроизвольно, то внутренняя энергия (энтальпия) должны уменьшаться, а энтропия увеличиваться. Для сравнения этих величин их надо выразить в одних единицах, а для этого Δ S умножить на T. В этом случае имеем Δ Н – энтальпийный фактор и Т Δ S -энтропийный фактор. В ходе реакции частицы стремятся к объединению, что ведет к уменьшению энтальпии (Δ Н < 0), с другой стороны – должна возрастать энтропия, т.е. увеличиваться число частиц в системе (Т Δ S > 0). "Движущая сила" реакции определяется разностью между этими величинами и обозначается Δ G. Δ G p,T = Δ H – T Δ S и называется изменением энергии Гиббса (изобарно-изотермический потенциал). Энергия Гиббса - это часть энергетического эффекта реакции, которую можно превратить в работу, поэтому ее называют свободной энергией. Это тоже термодинамическая функция состояния и, следовательно, для реакции b B + d D = l L + m M, энергию Гиббса химической реакции можно рассчитать как сумму энергий Гиббса образования продуктов реакции за вычетом энергий Гиббса образования исходных веществ с учетом стехиометрических коэффициентов по формуле: Δ G = l Δf G L + m Δf G M – d Δf G D – b Δf G B. где Δf G – энергия Гиббса образования веществ. Энергия Гиббса образования веществ это изменение энергии Гиббса системы при образовании 1 моль вещества из простых веществ, устойчивых при 298 К. Энергия Гиббса образования простых веществ Δf G принимается равной нулю. Если образующееся вещество и исходные простые вещества находятся в стандартных состояниях, то энергия Гиббса образования называется стандартной энергией Гиббса образования вещества Δf G 0. Ее значения приводятся в справочниках. Полученное значение Δ G является критерием самопроизвольного течения реакции в прямом направлении, если Δ G < 0. Химическая реакция не может протекать самопроизвольно в прямом направлении, если энергия Гиббса системы возрастает, т.е. Δ G > 0. Если Δ G = 0, то реакция может протекать как в прямом, так и в обратном направлениях, т.е. реакция обратима. Направление химических реакций зависит от их характера. Так, условие Δ G < 0 соблюдается при любой температуре для экзотермических реакций (Δ Н < 0), у которых в ходе реакции возрастает число молей газообразных веществ, и, следовательно, энтропия (Δ S > 0). У таких реакций обе движущие силы (Δ Н) и (Т Δ S) направлены в сторону протекания прямой реакции и Δ G < 0 при любых температурах. Такие реакции являются необратимыми.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 8439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.23.138 (0.008 с.) |

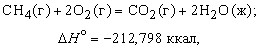
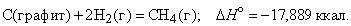
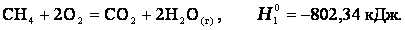

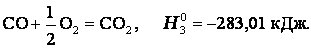
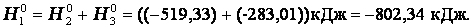
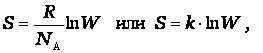
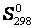 вещества, находящегося в стандартном состоянии при температуре 298,15 К. Т.к. энтропия является функцией состояния системы, то для реакции, протекающей в стандартных условиях,
вещества, находящегося в стандартном состоянии при температуре 298,15 К. Т.к. энтропия является функцией состояния системы, то для реакции, протекающей в стандартных условиях,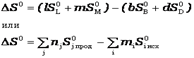 ,
, - стандартные энтропиипродуктов реакции и исходных веществ, соответственно.
- стандартные энтропиипродуктов реакции и исходных веществ, соответственно.


