
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прохождение частицы через потенциальный барьер. Туннельный эффект.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим простейший потенциальный барьер прямоугольной формы. Для одномерного (по оси х) движения частицы. ì∞,x<0 (для области 1) U(x)=í0,0≤x≤l (для области 2) î0,x>1 (для области 3) где l-ширина ямы, а энергия отсчитывается от ее дна, U-высота. Частица, обладая энергией Е, либо беспрепятственно пройдет над барьером(при Е>U), либо отразится от него (при Е<U) и будет двигаться в обратную сторону. Для микрочастица, даже при Е>U, имеется вероятность отражения от барьера, и при Е<U есть вероятность проникновения через барьер. Это слудет из решения ур-ния Шредингера, описывающего движение микрочастицы
для областей 1 и 3 k2=2mE/h2 ; для области 2 q2=2m(E-U)/h2 Общие решения этих диф.уравнений: Ψ1(x)=A1eikx+B1e-ikx(для области 1);Ψ2(x)=A2eiqx+B2e-iqx(для области2) Ψ3(x)=A3eikx+B3e-ikx(для области 3). В частности, для области 1 полная волновая, будет иметь вид ψ1(x,t)=ψ1(x)e-(i/h)Et=A1e-(i/h)(Et-px)+B1x-(i/h)(Et+px) (в этом выражении первый член представляет собой плоскую волну вдоль х, другой – волну, распространяющаяся в обратную сторону). В области 3 есть только прошедшая сквозь барьер волна и поэтому В3=0.Для области 2 q=iβ;β=√2m(E-U) /h. Получили Ψ1(x)=A1eikx+B1e-ikx, Ψ2(x)=A2e-βx+B2eβx,Ψ3(x)=A3eikx Качественный характер функций ψ1(х),ψ2(х),ψ3(х)(см.рис2), откуда следует, что волновая функция не равна нулю и внутри барьера, а в области3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой. Т.о. приходим к явлению – туннельный эффект, когда микрочастица может пройти сквозь потенциальный барьер.
2. Энергию
15.Уравнение Шредингера для гармонического осциллятора и анализ его решений. Линейный гармонический осциллятор – система, совершающая одномерное движение под действием квазиупругой силы – является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия осциллятора равна U=mω02x2/2 где ω0- собственная частота осциллятора,m- масса частицы. Гармонический осциллятор в квантовой механике – квантовый осциллятор – описывается уравнением Шредингера, учитывающим выражение для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются ур-нием Шредингера вида
где Е- полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что это уравнение решается только при собственных значениях энергии En=(n+½)ħω0. Эта формула показывает, что энергия квантового осциллятора может иметь только дискретные значения, т.е. квантуется. Строгое решение задачи о квантовом осцилляторе приводит еще к отличию от классического рассмотрения. Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области, в то время как с классической точки зрения она не может выйти за пределы области. Т.о. имеется отличная от нуля вероятность обнаружить частицу в области, которая является классически запрещенной. 2.надбарьерном отражении — отражению частицы с энергией, превосходящей высоту барьера. Этот результат является чисто квантовым и объясняется наличием у частицы волновых свойств. Макроскопическая частица, подчиняющаяся законам классической механики, при прохождении через низкий потенциальный порог не испытывает отражения, в области порога лишь уменьшается ее кинетическая энергия.
.16,.Представление физических величин операторами. Вычисление средних значений физических величин. А) Оператор координаты. Действие сводится к умножению волновой функции на эту координату: x^y=xy, y^y=yy, z^y=zy или x^=x… б) Оператор проекций импульса. Выражаются с помощью операторов дифференцирования по соответствующим координатам: P^x=(h/i)(¶/¶x), P^y=(h/i)(¶/¶y), P^z=(h/i)(¶/¶z),`p^={ P^x, P^y, P^z}. В) Оператор момента импульса:` L=`r´`p, Lx=ypz-zpy; Ly=zpy-xpz; Lz=xpy-ypx; L^x=y^p^z-z^p^y=(h/i)(y¶/¶x-z¶/¶y). Г) Оператор кинетической энергии. Определим T, пользуясь формулой Т=p2/2m, T^=p^2/2m=-h2/2m. Вычисление средних значений: L^y=Ly,<L>=òy*L^ydV, y(r)=Aexp(-r/a) 2. «Красная» грани́ца фотоэффе́кта — минимальная частота
где Aout — работа выхода для конкретного фотокатода, h — постоянная Планка, а с - скорость света. Работа выхода Aout зависит от материала фотокатода и состояния его поверхности. Испускание фотоэлектронов начинается сразу же, как только на фотокатод падает свет с частотой
17. Основные постулаты квантовой механики. Вероятностный характер результатов измерений в квантовой механике. Первый постулат квантовой механики. Состояние частицы в квантовой механике описывается заданием волновой функции y(x,y,z,t), являющейся функцией пространственных координат и времени. Вероятностный смысл волновой функции. Квадрат модуля волновой функции y(x,y,z,t) определяет плотность вероятности w того, что в момент времени t³0 частица может быть обнаружена в точке пространства M=M(x,y,z) с координатами x, y и z. w=dP/dV=|y|2=y*y. Волновую функцию, удовлетворяющую условию нормировки F®¥ò|y|2dV=1, называют нормированной волновой функцией. Условия регулярности волновой функции. 1. Условие конечности волновой функции (волновая функция была квадратично интегрируемой функцией). 2. Условие однозначности волновой функции (плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно). 3. Условие непрерывности волновой функции. Кроме того, непрерывными должны быть также частные производные волновой функции, т.е. функция должна быть гладкой. Принцип суперпозиции. Если частица может находиться в квантовом состоянии, описываемом волновой функцией y1, а также в другом квантовом состоянии, описываемом волновой функцией y2, и т.д. аналогично до yn, то эта частица может также находиться в состоянии, описываемом волновой функцией y=с1y1+с2y2+…+сnyn. В таком состоянии квадрат модуля коэффициента Сn определяет вероятность того, что при измерении, проведенном над системой с такой волновой функцией, мы обнаружим ее в квантовом состоянии, описываемом волновой функцией yn. Поэтому для нормированных волновых функций 2. Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии электромагнитного излучения с его частотой. Также имеет смысл кванта действия и кванта момента импульса. Впервые упомянута М. Планком в работе, посвящённой тепловому излучению, и потому названа в его честь.
Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.240 (0.007 с.) |

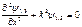


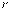 , приходящуюся на единичный диапазон частот, называют спектральной испускательной способностью тела или спектральной плотностью энергетической светимости. Испускательную способность тела можно представить и как функцию длины волны излучения
, приходящуюся на единичный диапазон частот, называют спектральной испускательной способностью тела или спектральной плотностью энергетической светимости. Испускательную способность тела можно представить и как функцию длины волны излучения 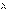 , которая связана с частотой
, которая связана с частотой 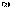 через скорость света в вакууме
через скорость света в вакууме  по формуле
по формуле  .
.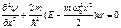
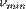 или максимальная длина волны λ max света, при которой еще возможен внешний фотоэффект, то есть начальная кинетическая энергия фотоэлектронов больше нуля. Частота
или максимальная длина волны λ max света, при которой еще возможен внешний фотоэффект, то есть начальная кинетическая энергия фотоэлектронов больше нуля. Частота  зависит только от работы выхода Aout электрона:
зависит только от работы выхода Aout электрона: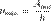
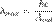
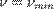 или с длиной волны
или с длиной волны 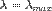 .
. .
.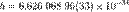 Дж·c
Дж·c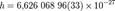 эрг·c.
эрг·c.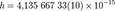 эВ·c.
эВ·c.


