Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 21. Прохождение через потенциальный барьер. Туннельный эффектСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопрос22. Уравнение Шредингера для атома водорода В лекции N 7 мы разобрали боровскую теорию атома водорода, основанную на постулатах Бора и условии стационарности состояний атома (4.3). Уравнение Шредингера, примененное к атому водорода, позволяет получить результаты боровской теории атома водорода без привлечения постулатов Бора и условия квантования. Квантование энергии возникает как естественное условие, появляющееся при решении уравнения Шредингера, в некотором смысле аналогичное причине квантования энергии для частицы в потенциальной яме. Применить стационарное уравнение Шредингера (7.3) к атому водорода это значит: а) подставить в это уравнение выражение для потенциальной энергии взаимодействия электрона с ядром б) в качестве m подставить me - массу электрона (если пренебречь, как и в лекции N 4, движением ядра). После этого получим уравнение Шредингера для атома водорода: Так как потенциальная энергия зависит только от r, решение уравнения удобно искать в сферической системе координат: r, θ, φ.(рис. 8.1)
Рис. 8.1 Волновая функция в этом случае будет функцией от r, θ и φ, т.е. Оператор Лапласа необходимо записать в сферических координатах, т.е. выразить через производные по r, θ и φ. Мы не будем этого делать, поскольку получение решения уравнения Шредингера для атома водорода не входит в программу курса общей физики. Приведем лишь результаты. Оказывается, что решение уравнения Шредингера для атома водорода существует при следующих условиях: а) при любых положительных значениях полной энергии (E > 0). Это так называемые несвязанные состояния электрона, когда он пролетает мимо ядра и уходит от него на бесконечность; б) при дискретных отрицательных значениях энергии Эта формула совпадает с полученной Бором формулой для энергии стационарных состояний атома водорода. Целое число n называют главным квантовым числом.
|
|||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 751; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

 Рис 7.4.1. – Движение частицы в поле прямоугольного потенциального барьера.
Такой вид поля получил название потенциального барьера. Область, в которой движется частица можно разбить на три области.
Рис 7.4.1. – Движение частицы в поле прямоугольного потенциального барьера.
Такой вид поля получил название потенциального барьера. Область, в которой движется частица можно разбить на три области.  Определить вероятность прохождения частицы, энергия которой меньше высоты потенциального барьера, из области I в область III без изменения энергии частицы. При движении частицы в I, II, III областях, скорость движения в пределах области остается постоянной. В таком случае движение микрочастицы описывается плоской волной де Бройля. На границе, где происходит скачкообразное изменение потенциала, эта волна должна себя вести аналогично электромагнитной волне на границе двух сред с разными показателями преломления. Волна на границе частично отражается частично проходит через границу. Таким образом, есть определенная вероятность обнаружить частицу в III области. Запишем уравнения Шрёдингера для каждой области отдельно:
для I и III (U =0):
Определить вероятность прохождения частицы, энергия которой меньше высоты потенциального барьера, из области I в область III без изменения энергии частицы. При движении частицы в I, II, III областях, скорость движения в пределах области остается постоянной. В таком случае движение микрочастицы описывается плоской волной де Бройля. На границе, где происходит скачкообразное изменение потенциала, эта волна должна себя вести аналогично электромагнитной волне на границе двух сред с разными показателями преломления. Волна на границе частично отражается частично проходит через границу. Таким образом, есть определенная вероятность обнаружить частицу в III области. Запишем уравнения Шрёдингера для каждой области отдельно:
для I и III (U =0):  , для II области (U
, для II области (U  0)
0) 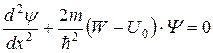 .
Решение дифференциальное уравнения для области I:
.
Решение дифференциальное уравнения для области I:  , где
, где  . Амплитуда «падающей» волны равна А 1, величина А2 1 – интенсивность «падающей» волны, В 1 – амплитуда «отраженной» волны, В2 1 – интенсивность «отраженной» волны. Для области II уравнение Шрёдингера имеет решение:
. Амплитуда «падающей» волны равна А 1, величина А2 1 – интенсивность «падающей» волны, В 1 – амплитуда «отраженной» волны, В2 1 – интенсивность «отраженной» волны. Для области II уравнение Шрёдингера имеет решение:  , где
, где 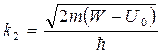 , А2 – амплитуда волны, проходящей в область II, В2 – амплитуда волны, отраженной от границы х = l. Для области III решение
, А2 – амплитуда волны, проходящей в область II, В2 – амплитуда волны, отраженной от границы х = l. Для области III решение  ,
,  (отраженной волны в третьей области нет),
(отраженной волны в третьей области нет),  , т.к. энергия прошедших через барьер частиц равна энергии падающих частиц, потерь энергии в барьере нет; А3 – амплитуда волны, прошедшей в область III,
, т.к. энергия прошедших через барьер частиц равна энергии падающих частиц, потерь энергии в барьере нет; А3 – амплитуда волны, прошедшей в область III,  – интенсивность волны, прошедшей, через потенциальный барьер. Отношение
– интенсивность волны, прошедшей, через потенциальный барьер. Отношение  – коэффициент отражения или вероятность того, что микрочастица отразится от потенциального барьера. Отношение
– коэффициент отражения или вероятность того, что микрочастица отразится от потенциального барьера. Отношение  – коэффициент прозрачности барьера или вероятность прохождения частицы через потенциальный барьер. Чтобы определить R и D, воспользуемся граничными условиями на
– коэффициент прозрачности барьера или вероятность прохождения частицы через потенциальный барьер. Чтобы определить R и D, воспользуемся граничными условиями на 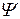 – функцию и ее производную на границах потенциального барьера, т.е. при х =0 и х =l. Эти условия следуют из условий непрерывности функции
– функцию и ее производную на границах потенциального барьера, т.е. при х =0 и х =l. Эти условия следуют из условий непрерывности функции  Коэффициент прозрачности барьера приблизительно равен:
Коэффициент прозрачности барьера приблизительно равен: 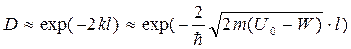 , где
, где  . Формула для коэффициента
. Формула для коэффициента 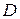 показывает, что проницаемость барьера в сильной степени зависит от ширины барьера
показывает, что проницаемость барьера в сильной степени зависит от ширины барьера  , массы микрочастицы и от разности «высоты» барьера и энергии частицы.
, массы микрочастицы и от разности «высоты» барьера и энергии частицы.