
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 14. Спектральные закономерности линейчатых спектров атома водорода. Спектральные серии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Простейший из атомов, атом водорода явился своеобразным тест-объектом для теории Бора. Ко времени создания теории Бора атом водорода был хорошо изучен экспериментально. Он содержит единственный электрон. Ядром атома является протон – положительно заряженная частица, заряд которой равен по модулю заряду электрона, а масса в 1836 раз превышает массу электрона. В 1890 году И. Ридберг получил эмпирическую формулу для частот спектральных линий: для серии Бальмера m = 2, n = 3, 4, 5,.... Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4,.... Постоянная R в этой формуле называется постоянной Ридберга. Ее численное значение R = 3,29·1015 Гц. До Бора механизм возникновения линейчатых спектров и смысл целых чисел, входящих в формулы спектральных линий водорода (и ряда других атомов), оставались непонятными. Постулаты Бора определили направление развития новой науки – квантовой физики атома. Но они не содержали рецепта определения стационарных состояний (орбит) и соответствующих им значений энергии En. Правило квантования, приводящее к правильным, согласующимся с опытом значениям энергий стационарных состояний атома водорода, было угадано Бором. Бор предположил, что момент импульса электрона, вращающегося вокруг ядра, может принимать только дискретные значения, кратные постоянной Планка. Для круговых орбит правило квантования Бора записывается в виде Здесь me – масса электрона, υ – его скорость, rn – радиус стационарной круговой орбиты. Правило квантования Бора позволяет вычислить радиусы стационарных орбит электрона в атоме водорода и определить значения энергий. Скорость электрона, вращающегося по круговой орбите некоторого радиуса r в кулоновском поле ядра, как следует из второго закона Ньютона, определяется соотношением где e – элементарный заряд, ε0 – электрическая постоянная. Скорость электрона υ и радиус стационарной орбиты rn связаны правилом квантования Бора. Отсюда следует, что радиусы стационарных круговых орбит определяются выражением
Самой близкой к ядру орбите соответствует значение n = 1. Радиус первой орбиты, который называется боровским радиусом, равен
Радиусы последующих орбит возрастают пропорционально n2. Полная механическая энергия E системы из атомного ядра и электрона, обращающегося по стационарной круговой орбите радиусом rn, равна
Следует отметить, что Ep < 0, так как между электроном и ядром действуют силы притяжения. Подставляя в эту формулу выражения для υ2 и rn, получим:
Целое число n = 1, 2, 3,... называется в квантовой физике атома главным квантовым числом. Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с энергией En на другую стационарную орбиту с энергией Em < En атом испускает квант света, частота νnm которого равна ΔEnm / h:
Эта формула в точности совпадает с эмпирической формулой Ридберга для спектральных серий атома водорода, если положить постоянную R равной
Подстановка числовых значений me, e, ε0 и h в эту формулу дает результат R = 3,29·1015 Гц, который очень хорошо согласуется с эмпирическим значением R. Рис. 9.3.1 иллюстрирует образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.
Рисунок 9.3.1. Стационарные орбиты атома водорода и образование спектральных серий.
Спектральные серии водорода — набор спектральных серий, составляющих спектр атома водорода. Поскольку водород — наиболее простой атом, его спектральные серии наиболее изучены. Они хорошо подчиняютсяформуле Ридберга: где R = 109 677 см−1 — постоянная Ридберга для водорода, n′ — основной уровень серии. Спектральные линии, возникающие при переходах на основной энергетический уровень, называются резонансными, все остальные — субординатными. Серия Лаймана[\ Открыта Т. Лайманом[en] в 1906 году. Все линии серии находятся в ультрафиолетовом диапазоне. Серия соответствует формуле Ридберга при n′ = 1 и n = 2, 3, 4, …; линияLα = 1216 Å является резонансной линией водорода. Граница серии — 911,8 Å. Серия Бальмера\ Открыта И. Я. Бальмером в 1885 году. Первые четыре линии серии находятся в видимом диапазоне и были известны задолго до Бальмера, который предложил эмпирическую формулу для их длин волн и на её основе предсказал существование других линий этой серии в ультрафиолетовой области. Серия соответствует формуле Ридберга при n′ = 2 и n = 3, 4, 5, …; линия Hα = 6565 Å, граница серии — 3647 Å. Серия Пашена Предсказана Ритцем в 1908 году на основе комбинационного принципа. Открыта Ф. Пашеном в том же году. Все линии серии находятся в инфракрасном диапазоне. Серия соответствует формуле Ридберга при n′ = 3 и n = 4, 5, 6, …; линия Pα = 18 756 Å, граница серии — 8206 Å. Серия Брэккета Открыта Ф. С. Брэккетом в 1922 году. Все линии серии находятся в ближнем инфракрасном диапазоне. Серия соответствует формуле Ридберга при n′ = 4 и n = 5, 6, 7, …; линияBα = 40 522 Å. Граница серии — 14 588 Å. Серия Пфунда Открыта А. Г. Пфундом в 1924 году. Линии серии находятся в ближнем (часть в среднем) инфракрасном диапазоне. Серия соответствует формуле Ридберга при n′ = 5 и n = 6, 7, 8, …; линия Pfα = 74 598 Å. Граница серии — 22 794 Å. Серия Хэмпфри Открыта К. Д. Хэмпфри в 1953 году. Серия соответствует формуле Ридберга при n′ = 6 и n = 7, 8, 9, …; основная линия — 123 718 Å, граница серии — 32 823 Å.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1026; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |



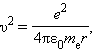







 ,
,


