
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория атома водорода по БоруСодержание книги Поиск на нашем сайте
6.1. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй. Ответ: 1,89 эВ. 6.2. Определить максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера). Ответ: Emax = 3,41 эВ, Emin = 1,89 эВ. 6.3. Определить длину волны λ, соответствующую второй спектральной линии в серии Пашена. Ответ: 1,28 мкм. 6.4. Максимальная длина волны спектральной водородной линии серии Лаймана равна 0,12 мкм. Предполагая, что постоянная Ридберга неизвестна, определить максимальную длину волны линии серии Бальмера. Ответ: 0,65 мкм. 6.5. Определить длину волны спектральной линии, соответствующую переходу электрона в атоме водорода с шестой боровской орбиты на вторую. К какой серии относится эта линия и которая она по счету? Ответ: 0,41 мкм. 6.6. Определить длины волн, соответствующие: 1) границе серии Лаймана; 2) границе серии Бальмера; 3) границе серии Пашена. Проанализировать результаты. Ответ: 1) 91 нм; 2) 364 нм; 3) 820 нм. 6.7. Атом водорода находится в возбужденном состоянии, характеризуемом главным квантовым числом n = 4. Определить возможные спектральные линии в спектре водорода, появляющиеся при переходе атома из возбужденного состояния в основное. Ответ: 1,21.10-7 м; 1,02.10-7 м; 0,97.10-7 м; 6,54.10-7 м; 4,85.10-7 м; 18,7.10-7 м. 6.8. В инфракрасной области спектра излучения водорода обнаружено четыре серии – Пашена, Брэкета, Пфунда и Хэмфри. Записать сериальные формулы для них и определить самую длинноволновую линию: 1) в серии Пашена; 2) в серии Хэмфри. Ответ: 1) 1,87 мкм, 2) 12,3 мкм. 6.9. Определить число спектральных линий, испускаемых атомарным водородом, возбужденным на n -й энергетический уровень. Ответ: N = n (n – 1)/2. 6.10. На дифракционную решетку с периодом d нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Оказалось, что в спектре дифракционный максимум k -гo порядка, наблюдаемый под углом φ, соответствовал одной из линий серии Лаймана. Определить главное квантовое число, соответствующее энергетическому уровню, с которого произошел переход. Ответ: n = (1 – ck /(R.d. sinφ))-1/2. 6.11. Используя теорию Бора для атома водорода, определить: 1) радиус ближайшей к ядру орбиты (первый боровский радиус); 2) скорость движения электрона по этой орбите. Ответ: 1) 52,8 пм; 2) 2,19 Мм/с. 6.12. Определить, на сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ = 4,86.10-7 м. Ответ: На 2,56 эВ. 6.13. Определить длину волны λ спектральной линии, излучаемой при переходе электрона с более высокого уровня энергии на более низкий уровень, если при этом энергия атома уменьшилась на ΔE = 10 эВ. Ответ: 124 нм. 6.14. Используя теорию Бора, определить орбитальный магнитный момент электрона, движущегося по третьей орбите атома водорода. Ответ: рm = en ħ/(2 m) = 2,8.10-23 А.м2. 6.15. Определить изменение орбитального механического момента электрона при переходе его из возбужденного состояния в основное с испусканием фотона с длиной волны λ = 1,02.10-7м. Ответ: Δ L = 2ħ = 2,1.10-34 Дж.с. 6.16. Позитроний – атомоподобная система, состоящая из позитрона и электрона, вращающегося относительно общего центра масс. Применяя теорию Бора, определить минимальные размеры подобной системы. Ответ: dmin = 2ε0 h2 /(π me2) = 106 пм. 6.17. Предполагая, что в опыте Франка и Герца вакуумная трубка наполнена не парами ртути, а разреженным атомарным водородом, определить, через какие интервалы ускоряющего потенциала φ возникнут максимумы на графике зависимости силы анодного тока от ускоряющего потенциала. Ответ: 10,2 В. 6.18. Используя постоянную Планка h, электрическую постоянную ε0, массу m и заряд е электрона, составить формулу для величины, характеризующей атом водорода по Бору и имеющей размерность длины. Указать, что это за величина. 6.19. Определить скорость υ электрона по третьей орбите атома водорода. Ответ: υ = e 2 / (4π.ε0. n. ħ) =0,731 Мм/с. 6.20. Электрон находится на первой боровской орбите атома водорода. Определить для электрона: 1) потенциальную энергию ЕP; 2) кинетическую энергию ЕK; 3) полную энергию Е. Ответ: 1) -27,2 эВ; 2) 13,6 эВ; 3) -13,6 эВ. 6.21. Определить частоту f вращения электрона по третьей орбите атома водорода, Ответ: f = mе 4 / (4 n 3.ε02 .h 3) = 2,42.1014 Гц. 6.22. Определить: 1) частоту f вращения электрона, находящегося на первой боровской орбите; 2) эквивалентный ток. Ответ: 1) 6,58.1015 Гц; 2) 1,06 мА. 6.23. Определить частоту света, излучаемого атомом водорода, при переходе электрона на уровень с главным квантовым числом n = 2, если радиус орбиты электрона изменился в k = 9 раз. Ответ: 0,73.1015 Гц. 6.24. Пользуясь теорией Бора, найти числовое значение постоянной Ридберга. Ответ: R = m . е 4 / (8ε02. h 3) = 3,27.1014 с-1. 6.25. Определить потенциал ионизации атома водорода Ответ: 13,6 В. 6.26. Основываясь на том, что энергия ионизации атома водорода Еi = 13,6 эВ, определить первый потенциал возбуждения φ этого атома. Ответ: 10,2 В. 6.27. Определить первый потенциал возбуждения атома водорода. Ответ: φ1 = 3 R . h / (4 e) = 10,2 В. 6.28. Основываясь на том, что энергия ионизации атома водорода Еi = 13,6 эВ, определить в электрон-вольтах энергию фотона, соответствующую самой длинноволновой линии серии Бальмера. Ответ: 1,89 эВ. 6.29. Основываясь на том, что первый потенциал возбуждения атома водорода φ1 = 10,2 В, определить в электронвольтах энергию фотона, соответствующую второй линии серии Бальмера. Ответ: 2,55 эВ. 6.30. Определить работу, которую необходимо совершить, чтобы удалить электрон со второй боровской орбиты атома водорода за пределы притяжения его ядром. Ответ: 5,45.10-19 Дж. 6.31. Электрон выбит из атома водорода, находящегося в основном состоянии, фотоном энергии ε = 17,7 эВ. Определить скорость электрона за пределами атома. Ответ: 1,2 Мм/с. 6.32. Фотон с энергией E = 12,12 эВ, поглощенный атомом водорода, находящимся в основном состоянии, переводит атом в возбужденное состояние. Определить главное квантовое число этого состояния. Ответ: 3. 6.33. Определить, какие спектральные линии появятся в видимой области спектра излучения атомарного водорода под действием ультрафиолетового излучения с длиной волны λ = 0,1 мкм. Ответ: 4,34.10-7 м; 4,86.10-7 м; 6,56.10-7 м. 6.34. В излучении звезды обнаружен водородоподобный спектр, длины волн которого в 9 раз меньше, чем у атомарного водорода. Определить элемент, которому принадлежит данный спектр. Ответ: Z = 3, литий. 6.35. Применяя теорию Бора к мезоатому водорода (в мезоатоме водорода электрон заменен мюоном, заряд которого равен заряду электрона, а масса в 207 раз больше массы электрона), определить: 1) радиус первой орбиты мезоатома; 2) энергию ионизации мезоатома. Ответ:1) 0,254 пм; 2) 2,81 кэВ. 6.36. Определить, какая энергия требуется для полного отрыва электрона от ядра однократно ионизованного атома гелия, если: 1) электрон находится в основном состоянии; 2) электрон находится в состоянии, соответствующем главному квантовому числу n = 3. Ответ: 1) 54,4 эВ; 2) 6,04 эВ.
Элементы квантовой механики 7.1. Определить импульс и энергию: 1) рентгеновского фотона; 2) электрона, если длина волны того и другого равна 10-10м. Ответ: 1) р =6,63.10-24 кг.м/с, E =12,4 кэВ; 2) р = 6,63·10-24 кг.м/с, Е = 151 эВ. 7.2. Определить длину волны де Бройля для электрона, находящегося в атоме водорода на третьей боровской орбите. Ответ: 1 нм. 7.3. Определить длину волны де Бройля для нейтрона, движущегося со средней квадратичной скоростью при Т = 290 К. Ответ: 148 пм. 7.4. Протон движется в однородном магнитном поле с индукцией B = 15 мТл по окружности радиусом R = 1,4 м. Определить длину волны де Бройля для протона. Ответ: 0,197 пм. 7.5. Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля λ для него была равна 1 нм. Ответ: 0,821 мВ. 7.6. Заряженная частица, ускоренная разностью потенциалов U = 500 В, имеет длину волны де Бройля λ = 1,282 нм. Принимая заряд этой частицы равным заряду электрона, определить ее массу. Ответ: 1.672.10-27 кг. 7.7. Кинетическая энергия электрона равна 1 кэВ. Определить длину волны де Бройля. Ответ: 38,8 пм. 7.8. Кинетическая энергия электрона равна 0,6 МэВ. Определить длину волны де Бройля. Ответ: 1,26 пм. 7.9. Определить, при каком числовом значении скорости длина волны де Бройля для электрона равна его комптоновской длине волны. Ответ: υ = 2,12·108 м/с. 7.10. Вывести связь между длиной круговой электронной орбиты и длиной волны де Бройля. 7.11. Определить, как изменится длина волны де Бройля электрона атома водорода при переходе его с четвертой боровской орбиты на вторую. Ответ: Уменьшится в 2 раза. 7.12. В опыте Дэвиссона и Джермера, обнаруживших дифракционную картину при отражении пучка электронов от естественной дифракционной решетки – монокристалла никеля, оказалось, что в направлении, составляющем угол α = 55° с направлением падающих электронов, наблюдается максимум отражения четвертого порядка при кинетической энергии электронов Т = 180 эВ. Определить расстояние между кристаллографическими плоскостями никеля. Ответ: d = h . k / (2 7.13. Моноэнергетический пучок нейтронов, получаемый в результате ядерной реакции, падает на кристалл с периодом d = 0,15 мм. Определить скорость нейтронов, если брэгговское отражение первого порядка наблюдается, когда угол скольжения Θ = 30°. Ответ: 2,64 км/с. 7.14. Параллельный пучок моноэнергетических электронов направлен нормально на узкую щель шириной а = 1 мкм. Определить скорость этих электронов, если на экране, отстоящем на расстоянии l = 20 см от щели, ширина центрального дифракционного максимума составляет Δ x = 48 мкм. Ответ: υ = 2 hl / (am .Δ x) = 606 км/с. 7.15. Параллельный пучок электронов, ускоренный разностью потенциалов U = 50 В, направлен нормально на две параллельные, лежащие в одной плоскости, щели, расстояние d между которыми равно 10 мкм. Определить расстояние между центральным и первым максимумами дифракционной картины на экране, который расположен от щелей на расстоянии l = 0,6 м. Ответ: Δ x = 2 hl / (d 7.16. Объяснить, почему представление о боровских орбитах несовместимо с принципом неопределенности. 7.17. Ширина следа электрона (обладающего кинетической энергией Т = 1,5 кэВ) на фотопластинке, полученного с помощью камеры Вильсона, составляет Δ x = 1 мкм. Определить, можно ли по данному следу обнаружить отклонение в движении электрона от законов классической механики. Ответ: Δ px / px = 10-4, нет. 7.18. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 1 кВ. Известно, что неопределенность скорости составляет 0,1 % от ее числового значения. Определить неопределенность координаты электрона. Являются ли электроны в данных условиях квантовыми или классическими частицами? Ответ: Δ x = 38,8 нм. 7.19. Определить отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10-5 м, и пылинки массой m = 10-12 кг, если ее координата установлена с такой же точностью. Ответ: 1,1·1018. 7.20. Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 нм (с точностью порядка диаметра атома) и его скорость с точностью до 10 %. Ответ: m .Δυ.Δ x < h; нет. 7.21. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10 % от ее числового значения, определить неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории? Ответ: Δ x = 3,34 нм, нет. 7.22. Применяя соотношение неопределенностей, показать, что для движущейся частицы, неопределенность координаты которой равна длине волны де Бройля, неопределенность скорости равна по порядку величины самой скорости частицы. 7.23. Используя соотношение неопределенностей в форме Δ px .Δ x ≥ ħ, оценить минимально возможную полную энергию электрона в атоме водорода. Принять неопределенность координаты равной радиусу атома. Сравнить полученный результат с теорией Бора. Ответ: Emax = – me 4 / (8 h 2.ε02) = -13,6 эВ. 7.24. Объяснить физический смысл соотношения неопределенности для энергии E и времени t: Δ E .Δ t ≥ h. 7.25. Воспользовавшись соотношением неопределенностей, оценить размытость энергетического уровня в атоме водорода: 1) для основного состояния; 2) для возбужденного состояния (время его жизни равно 10-8с). Ответ: 1) 0; 2) 414 нэВ. 7.26. Длина волны λ излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния Δ t = 10-8 c, определить отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом. Ответ: Δ Е / Е = λ / (c .Δ t) = 2.10-7. 7.27. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определить (в электрон-вольтах) неопределенность энергии этого электрона. Ответ: Δ Е = h2 / 2 m . (Δ x) 2 = 16,7 эВ. 7.28. Объяснить, почему физический смысл имеет не сама ψ -функция, а квадрат ее модуля |ψ|2. 7.29. Объяснить, почему волновая функция должна быть конечной, однозначной и непрерывной. 7.30. Записать выражение для вероятности W обнаружения частицы в конечном объеме V, если известна координатная пси-функция частицы ψ(x, y, z). 7.31. Известно, что свободная квантовая частица описывается плоской монохроматической волной де Бройля. Плотность вероятности (вероятность, отнесенная к единице объема) обнаружения свободной частицы |ψ|2 = ψψ* = | А |2 = const. Объяснить, что означает постоянство этой величины. 7.32. Записать уравнение Шредингера для стационарных состояний для свободной частицы, движущейся вдоль оси х, а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? Ответ: E = ħ2. k 2 / (2 m). 7.33. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в основном состоянии. Определить вероятность обнаружения частицы в левой трети «ямы». Ответ: 0,195. 7.34. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 2). Определить вероятность обнаружения частицы в области 3/8 l ≤ х ≤ 5/8 l. Ответ: 0,091. 7.35. Электрон находится в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками». Определить вероятность W обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 3). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии. Ответ: 1/3. 7.36. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 3). Определить, в каких точках «ямы» (0 ≤ х ≤ 1) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Пояснить полученный результат графически. Ответ: 1) l /6, l /2, 5 l /6; 2) l /3, 2 l /3. 7.37. Определить, при какой ширине одномерной прямоугольной «потенциальной ямы» с бесконечно высокими «стенками» дискретность энергетического спектра электрона сравнима с его средней кинетической энергией при температуре Т. Ответ: l = ħ.π / 7.38. Доказать, что энергия свободных электронов в металле не квантуется. Принять, что ширина l прямоугольной «потенциальной ямы» с бесконечно высокими «стенками» для электрона в металле составляет 10 см. Ответ: Δ E ≈0,75 n .10-16 эВ. 7.39. Частица находится в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Определить, во сколько раз изменяется отношение разности соседних энергетических уровней частицы: 7.40. Частица с энергией E движется в положительном направлении оси x и встречает на своем пути прямоугольный потенциальный барьер высотой U и конечной шириной l, причем E < U. Записать уравнение Шредингера для областей 1, 2 и 3. 7.41. Электрон с энергией Е = 4 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определить коэффициент D прозрачности потенциального барьера. Ответ: 0,1. 7.42. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Определить в электрон-вольтах разность энергий (U – E), при которой вероятность прохождения электрона сквозь барьер составит 0,5. Ответ: 0,454 эВ. 7.43. Протон с энергией Е = 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определить: 1) вероятность прохождения протоном этого барьера; 2) во сколько раз надо сузить барьер, чтобы вероятность прохождения его протоном была такой же, как для электрона при вышеприведенных условиях. Ответ: 1) 1,67.10-43; 2) в 42,9 раза. 7.44. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси х электрона U – E = 5 эВ. Определить, во сколько раз изменится коэффициент D прозрачности потенциального барьера для электрона, если разность U – E возрастет в 4 раза. Ответ: Уменьшится в 10 раз. 7.45. Электрон с длиной волны де Бройля λ1 = 100 нм, двигаясь в положительном направлении оси х, встречает на своем пути бесконечно широкий прямоугольный барьер высотой U = 100 эВ. Определить длину волны де Бройля после прохождения барьера. Ответ: λ2 = λ1 / 7.46. Частица с энергией Е = 50 эВ, двигаясь в положительном направлении оси х, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 20 эВ. Определить вероятность отражения электрона от этого барьера. Ответ: W = 0,016. 7.47. Частица массой m = 10-19 кг, двигаясь в положительном направлении оси х со скоростью υ = 20 м/с, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определить коэффициент отражения R волн де Бройля на границе потенциального барьера. Ответ: R = 0,146. 7.48. Электрон с длиной волны λ де Бройля, равной 120 пм, движется в положительном направлении оси x и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 200 эВ. Определить коэффициент отражения R волн де Бройля на границе потенциального барьера. Ответ: R = l. 7.49. Объяснить физический смысл существования энергии нулевых колебаний для квантового гармонического осциллятора. Зависит ли наличие нулевых колебаний от формы «потенциальной ямы»? 7.50. Математический маятник можно рассматривать в качестве гармонического осциллятора. Определить в электрон-вольтах энергию нулевых колебаний для маятника длиной l = 1 м, находящегося в поле тяготения Земли. Ответ: 1,03.10-15 эВ. 7.51. Рассматривая математический маятник массой m = 100 г и длиной l = 0,5м в виде гармонического осциллятора, определить классическую амплитуду А маятника, соответствующую энергии нулевых колебаний этого маятника. Ответ: А =
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.5.248 (0.012 с.) |

 cos(α/2)) = 0,206 нм, k – порядок максимума.
cos(α/2)) = 0,206 нм, k – порядок максимума. ) = 10,4 мкм.
) = 10,4 мкм. .
.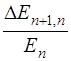 при переходе от n = 3 к n' = 8. Объяснить физическую сущность полученного результата. Ответ: Уменьшается в 3 раза.
при переходе от n = 3 к n' = 8. Объяснить физическую сущность полученного результата. Ответ: Уменьшается в 3 раза. = 172 пм.
= 172 пм.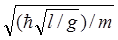 = 1,54.10-17 м.
= 1,54.10-17 м.


