
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантование отсчетов по уровнюСодержание книги Поиск на нашем сайте
Квантование по уровню применяется для получения конечного числа амплитудных значений дискретных отсчетов сигнала взамен непрерывного бесконечно большого количества их значений, т. е. процесс квантования аналогичен процедуре округления числа до ближайшего разрешенного значения. Такое округление всегда связано с погрешностью, называемой погрешностью квантования. В результате квантования возникают специфические нелинейные искажения, действие которых на передаваемый сигнал можно условно представить как добавление к неискаженному сигналу некоторой аддитивной помехи – шума квантования. Эти искажения неустранимы, но практически могут быть сделаны неощутимыми для получателя сообщений при надлежащем выборе числа уровней округляемой (квантуемой) величины сигнала. В зависимости от разбивки динамического диапазона сообщения на уровни квантования различают равномерное (линейное) и неравномерное (нелинейное) квантования. В первом случае на всем динамическом диапазоне сообщения шаг квантования выбирается одинаковым. На рисунке 2, а показан процесс квантования, а на рисунке 7 показана амплитудная характеристика квантующего устройства с равномерной шкалой квантования. Характеристика U вых = f (U λ) квантующего устройства имеет два характерных участка: зону квантования и зону ограничения. Для первого участка – U 0≤ U λ ≤ U 0, а для второго | U λ| > | U 0|. В соответствии с этим кроме шумов квантования различают еще и шумы ограничения, которые вызываются ограничением максимальных мгновенных значений сигнала. Обычно уровень сигнала на входе каналов системы ИКМ выбирается так, чтобы с учетом статистических характеристик входного сигнала вероятность превышения | U λ макс| > | U 0| была достаточно малой, поэтому определяющими в системах ИКМ являются шумы квантования, а не шумы ограничения. Средняя мощность шумов квантования при постоянном шаге обычно определяется как Р ш кв = Δλ2 /12. Как видно из рисунка 7, недостаток равномерной шкалы квантования заключается в том, что относительная погрешность квантования, т. е. отношение εкв(t)/λ(t), для сильных сигналов мала, в то время как для слабых сигналов она велика.
Рисунок 7 – Амплитудная характеристика квантующего устройства
При передаче речевых сигналов наиболее вероятны сигналы с малыми мгновенными значениями, поэтому для передачи их с меньшей погрешностью необходимо уменьшить шаг квантования. Обычно требуют, чтобы защищенность речевого сигнала от шума квантования была не менее 20 дБ на минимальном уровне средней мощности. Под защищенностью понимают
A кв = 10 lg (P с/ P ш кв),
где P с – мощность сигнала; P ш кв – мощность шумов квантования.
При равномерном квантовании для получения требуемой защищенности от шумов квантования при передаче речевых сигналов кодирование должно производиться достаточно большим числом разрядов кода, что нежелательно. При увеличении числа разрядов кода уменьшается длительность импульсов и соответственно расширяется спектр сигнала ИКМ, усложняются устройства кодирования и декодирования, увеличиваются требования к их быстродействию. Таким образом, недостатком равномерного квантования является то, что защищенность от шумов квантования A кв минимальна для наиболее слабых сигналов и увеличивается пропорционально увеличению уровня сигнала. Для выравнивания величины A кв при изменении уровня сигнала в широких пределах и соответственно для уменьшения количества уровней квантования и уменьшения разрядности двоичного кода применяют неравномерное квантование, при котором шаг квантования имеет минимальное значение для слабых сигналов и увеличивается с увеличением уровня входного сигнала (рисунки 8 и 9).
Рисунок 8 – Абсолютная (eкв) и относительная погрешности
Нелинейная шкала квантования в системах передачи с ИКМ может быть реализована несколькими способами: сжатием динамического диапазона сигнала перед кодированием, для чего используются компрессоры, и последующим его расширением после декодирования с помощью экспандеров; нелинейным кодированием и декодированием; цифровым компандированием.
Рисунок 9 – Амплитудная характеристика квантующего устройства
При неравномерном квантовании непрерывных сигналов обычно ставится задача: выбором закона изменения шага квантования обеспечить примерно равное отношение сигнал – шум квантования в достаточно широком диапазоне уровней входных сигналов. Если шаг квантования будет возрастать по мере увеличения входного сигнала, то по сравнению с равномерным квантованием для слабых сигналов отношение сигнал – шум возрастет, а для сильных снижается, оставаясь, однако, достаточно высоким. Рассмотрим один из возможных способов осуществления неравномерного квантования – с использованием аналоговых компандеров. На рисунке 10 показаны амплитудные характеристики U вых = f (U λ) аналоговых компрессора и эспандера. Компрессор представляет собой устройство с нелинейной амплитудной характеристикой, называемой характеристикой компрессии. Слабые сигналы компрессор усиливает в большей степени, чем
Применение неравномерного квантования позволяет обеспечить требуемую защищенность от шумов квантования для наиболее слабых речевых сигналов при восьмиразрядном кодировании вместо двенадцатиразрядного при равномерном квантовании. Недостатком аналогового компандирования является сложность получения с большой точностью взаимообратных амплитудных характеристик компрессора и экспандера, вследствие чего нелинейность суммарной амплитудной характеристики приводит к нелинейным искажениям передаваемых сигналов. Необходимое качество передачи сигналов в реальных условиях достигается путем применения неравномерных кодирующих и декодирующих устройств (методами нелинейного кодирования), когда формирование неравномерной квантующей характеристики осуществляется непосредственно в кодере (декодере). Последний в этом случае называется нелинейным. Наибольшее распространение в системах ИКМ получили нелинейные кодеки (обычно кодер и декодер объединяются в устройство, называемое кодеком) взвешивающего типа с цифровым компандированием эталонов. В таких кодеках характеристика компрессии (экспандирования) не является непрерывной, (аналоговой), а представляется ломаной, состоящей из прямолинейных отрезков (сегментов), приближенно представляющих (аппроксимирующих) заданный закон сжатия и расширения динамического диапазона сигналов. Необходимая форма характеристики компрессии (сжатия) и экспандирования (расширения) в кодеках формируется с помощью цифровых логических устройств, управляющих переключением эталонов. Наиболее распространенными для кодеров с неравномерным шагом квантования являются два приблизительно равноценных закона компрессии А и μ, с помощью которых получается квазилогарифмическая характеристика компрессора. Характеристика компрессии закона А описывается следующими уравнениями:
где sign(λ) – полярность сигнала; λ– амплитуда входного сигнала; А – параметр, используемый для определения степени компрессирования.
Характеристика FA (λ) имеет особое свойство, которое заключается в возможности хорошей ее аппроксимации ломаной линией, что значительно упрощает процесс преобразования. В качестве международного стандарта для нелинейных кодеров взвешивающего типа принята сегментная характеристика компандирования типа А = 87.6/13, показанная на рисунке 11. Характеристика компрессии в положительной области содержит сегменты С 0, С 1, С 2... С 7 и ограничена точками (узлами): 0-1; 1-2; 2-3;...7-8. Аналогичным образом строится характеристика для отрицательной области значений входного сигнала. Четыре сегмента - С 1,- С 0, С 0, С 1 (два в положительной и два в отрицательной областях) объединяются в один центральный сегмент, поэтому общее количество сегментов на двухполярной характеристике равно 13. Каждый из 16 сегментов характеристики содержит по 16 шагов (уровней квантования), а общее число уровней равно 256, из них 128 положительных и 128 отрицательных. Шаг квантования внутри каждого сегмента равномерный, а величина шага при переходе от одного сегмента к другому изменяется вдвое, начиная с центрального. Для С 0, С 1, С 2,... С 7 значения шагов квантования соответственно равны 2, 2, 4, 8, 16, 32, 64, 128 условных единиц. При изменении шага квантования дискретно изменяется крутизна характеристики в точках ее излома (узлах). Четыре сегмента - С 1, - С 0, С 0 и С 1 имеют одинаковую крутизну и равные шаги квантования. При таком построении характеристики наименьший (минимальный) шаг квантования Δλмин имеют сегменты - С 1, - С 0, С 0 и С 1, а наибольший Δλмакс – сегмент С7, причем отношение Δλмакс /Δλмин составляет 26 или 64. Эта величина характеризует параметр сжатия (расширения) для сегментной характеристики компандирования, или параметр А.
Рисунок 11 – Сегментная характеристика компрессии закона А = 87,6/13 (для положительной области)
Эффективность рассмотренной характеристики можно оценить визуально, если обратить внимание на то, что 112 уровней из 128 используются для квантования сигналов, амплитуда которых не превышает 50% максимальной, а 64, или 50% уровней, – для квантования сигналов, амплитуда которых не превышает 6.2% максимальной. Рассмотренная характеристика по погрешности квантования эквивалентна характеристике равномерного квантователя с 4096 уровнями, для кодирования которых потребовалось бы двенадцатиразрядная кодовая комбинация. При нелинейном кодировании число уровней квантования составляет 128, а разрядность кодовой комбинации при тех же условиях равна 8. При 128 значениях уровней нелинейное кодирование осуществляется за 8 тактов и включает три основных этапа: 1 – определение и кодирование полярности входного сигнала, определяется на первом такте (если положительный, то указывается 1, отрицательный – 0); 2 – определение и кодирование номера сегмента, в котором находится кодируемый отсчет, например: 0, если отсчет находится в сегменте 0; 1, если отсчет находится в сегменте 1; 2, если отсчет находится в сегменте 2 и т. д. Номер сегмента или узла, соответствующего номеру этого сегмента, характеристики компрессии, в котором находится отсчет, указывается в двоичном коде во втором, третьем и четвертом тактах кодирования; 3 – определение и кодирование номера уровня квантования сегмента, в зоне которого заключена амплитуда кодируемого отсчета (происходит в 5, 6, 7 и 8-м тактах кодирования). Этот этап осуществляется в четыре такта методом линейного кодирования. Здесь следует помнить, что шаг квантования внутри сегмента равномерный, число шагов квантования равно 16. Номер уровня квантования кодируемого отсчета внутри соответствующего сегмента представляется в двоичном коде. При декодировании осуществляется обратное цифро-аналоговое преобразование сигналов. Особенность нелинейного декодера заключается в формировании характеристики экспандера, обратной по своему характеру характеристике компрессии. На рисунке 11 часто вместо относительной величины U λ/ U макс конечные точки сегментов для целочисленного представления даются, исходя из максимальной амплитуды сигнала (U макс = DC – динамический диапазон сигнала), равной 4096 условным единицам. Конечные точки сегментов при кодировании с компрессированием по закону А равны 32, 64, 128, 256, 512, 1024, 2048, 4096 условным единицам. В соответствии с этим для отсчета с абсолютным значением λ можно найти его значение в условных единицах по формуле
Номер сегмента квантованного отсчета С определяется как наименьшее целое из выражения
при С = 0, 1, 2, … 7.
После вычисления С может быть определен остаток r – разность между амплитудой входного сигнала (в условных единицах) и величиной, соответствующей нижней конечной точке данного сегмента
Номер уровня квантования отсчета в сегменте К определяется как наименьшее целое из выражения
где K = 0, 1, 2, … 15.
После того как С и К определены, они представляются числами в двоичной системе счисления из трех и четырех разрядов соответственно. Абсолютное значение квантованного отсчета в условных единицах на выходе кодера при законе компрессии А можно определить как
Абсолютное значение квантованного отсчета в единицах измерения входного сигнала определяется по формуле
Погрешность (абсолютная) квантования равна
Относительная погрешность квантования определяется по формуле
Шаг квантования
где
Характеристика компрессии закона
где sign(
Для упрощения процесса преобразования выбирается специальная характеристика компрессии с Для удобства описания алгоритмов кодирования и декодирования предлагается использовать целочисленные представления, при которых аналоговые сигналы сводятся к одному масштабу с максимальной амплитудой, равной 8159 условных единиц. Конечные точки сегментов (узлы) при кодировании с компрессией по закону В соответствии с этим для отсчета с абсолютным значением
Номер сегмента квантованного отсчета С определяется как наименьшее целое из выражения
где С = 0, 1, 2,... 7.
Рисунок 12 – Сегментная характеристика компрессии с μ=255/15 (первые четыре сегмента)
После вычисления С может быть определен остаток r – разность между амплитудой входного сигнала и величиной, соответствующей нижней конечной точке данного сегмента.
Номер уровня квантования отсчета в сегменте К определяется как наименьшее целое из выражения
где K = 0, 1, 2, … 15.
Отметим, что при этом процессе уровни квантования K в сегменте С = 0 определяются как имеющие значения, равные 1, 3, 5... 31, в то время как в других сегментах уровни квантования определяются значениями, кратными 4, 8, 16, 32, 64, 128, 256 (соответственно для С = 1, 2, 3, 4, 5, 6, 7). После того как С и К определены, они представляются числами в двоичной системе счисления из трех и четырех разрядов соответственно. Абсолютное значение квантованного отсчета в условных единицах на выходе кодера при законе компрессии
Абсолютное значение квантованного отсчета в единицах измерения входного сигнала определяется по формуле
Результаты кодирования и декодирования по законам А = 87.6/13 и Таблица 1 – Кодирование (декодирование) для сегментной
Таблица 2 – Кодирование (декодирование) для сегментной
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.122 (0.008 с.) |




 Применение компрессора перед кодером с равномерным квантованием позволяет получить неравномерное квантование. На приемном конце после декодера сигнал поступает на экспандер, имеющий обратную компрессору амплитудную характеристику, при этом суммарная амплитудная характеристика должна быть линейной. Экспандер устраняет искажения, вносимые в сигнал компрессором, так что результирующая амплитудная характеристика сигнала «компрессор-экспандер» является линейной. Система, состоящая из последовательно включенных компрессора и экспандера, называется компандером.
Применение компрессора перед кодером с равномерным квантованием позволяет получить неравномерное квантование. На приемном конце после декодера сигнал поступает на экспандер, имеющий обратную компрессору амплитудную характеристику, при этом суммарная амплитудная характеристика должна быть линейной. Экспандер устраняет искажения, вносимые в сигнал компрессором, так что результирующая амплитудная характеристика сигнала «компрессор-экспандер» является линейной. Система, состоящая из последовательно включенных компрессора и экспандера, называется компандером.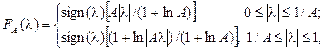 (10)
(10)
 . (11)
. (11)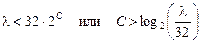 , (12)
, (12) (13)
(13) или
или  (14)
(14) (15)
(15) (16)
(16) (17)
(17)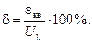 (18)
(18) изменяется при переходе от сегмента к сегменту и в зависимости от номера сегмента определяется выражением
изменяется при переходе от сегмента к сегменту и в зависимости от номера сегмента определяется выражением
 – шаг квантования на центральном сегменте, Dlмин = 2 у.е.;
– шаг квантования на центральном сегменте, Dlмин = 2 у.е.; ─ порог ограничения кодера,
─ порог ограничения кодера,  описывается следующим уравнением
описывается следующим уравнением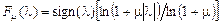 , (19)
, (19)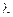 ) – полярность сигнала;
) – полярность сигнала; . (20)
. (20) , (21)
, (21)
 (22)
(22) или
или  (23)
(23) (24)
(24) (25)
(25)


