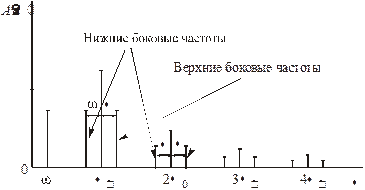Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретизация непрерывных сообщенийСодержание книги Поиск на нашем сайте
Преобразование аналогового сигнала в дискретный называется дискретизацией. В результате ее получается амплитудно-импульсный сигнал (АИМ). Различают амплитудную импульсную модуляцию первого (АИМ-1) и второго рода (АИМ-2). При АИМ-1 амплитуда импульса следует за изменениями модулирующего сообщения в течение всего времени существования этого импульса (рисунок 4, в). Модулированная последовательность в этом случае определяется U (t) = U 0 [1 + m АИМ λ(t)] где U 0 – амплитуда немодулированных прямоугольных импульсов; S 0(t) = U 0 S (t) – нормированная функция, выражающая форму импульса; ti = iТ 0 + t н – момент появления i -го импульса относительно t = 0 (i = 1, 2, 3,...); t н – величина, характеризующая положение начального импульса; m АИМ – коэффициент глубины модуляции импульсов.
В случае АИМ-2 амплитуда импульса определяется мгновенным значением сообщения, взятым в момент ti = iТ 0, и сохраняется постоянной во время импульса (рисунок 4, г).
Рисунок 4 – Формирование амплитудно-импульсного сигнала
Модулированный сигнал АИМ-2 можно записать следующим образом: U (t) =
Определим спектр сигнала АИМ-1, если модулирующий (дискретизируемый) сигнал имеет вид λ(t) = U cos ω t, где U – амплитуда гармонического сигнала (U = 1 В). В этом случае выражение (4) принимает вид
U (t) = U 0 [1 + m АИМ cos ω t ]
Так как функция S 0(t) периодическая, ее можно разложить в ряд Фурье
где ω0 = 2π/ Т 0 = 2π f 0 – круговая частота основной (первой) гармоники прямоугольных импульсов (частота дискретизации), рад/с; An =
φ n – начальная фаза n -й гармоники.
Таким образом, спектр несущего колебания содержит постоянную составляющую и гармоники частоты дискретизации. Подставляя выражение (7) в равенство (6), получим
или после обычных преобразований
U (t) = a 0/2 + 1/2 m АИМ a 0cosω t + + 1/2 m АИМ + 1/2 m АИМ Если модулирующий (дискретизируемый) сигнал имеет вид λ(t) = U
где | A (j ω)| – модуль спектральной плотности немодулированных импульсов. Для прямоугольного импульса модуль спектральной плотности амплитуд A (ω) = | A (j ω)| =
где t и – длительность прямоугольного импульса.
При ω = 0 модуль спектральной плотности | A (j ω)| = U 0 t и. Поскольку модуль спектральной плотности | A (j ω)| входит в общей форме в выражение (9), оно пригодно для расчета частотных спектров при любой форме немодулированных импульсов. Из формул (8) и (9) видно, что спектр АИМ сигнала состоит из постоянной составляющей, спектральной составляющей, имеющей частоту ω модулирующего сигнала, и ряда боковых частот типа Общий характер спектров сигналов АИМ-1 и АИМ-2 одинаков. В обоих случаях в составе спектра имеется составляющая с частотой ω. Есть и различия, которые сводятся к следующему. При АИМ-1 амплитуды колебаний двух боковых частот, симметрично расположенных по обе стороны каждой гармоники частоты дискретизации, равны между собой и определяются значением спектральной плотности одиночного импульса Ап. При АИМ-2 эти амплитуды различны и определяются значениями А (n ω0 ± ω). Что касается спектральной составляющей с частотой ω, то при АИМ-1 ее амплитуда пропорциональна а 0, а при АИМ-2 – А (ω). Указанные различия между АИМ-1 и АИМ-2 становятся незначительными если модулирующее сообщение за время существования импульса изменяется мало. Это происходит при уменьшении длительности импульсов t и. В пределе, при t и → 0, различие между АИМ-1 и АИМ-2 пропадает.
Рисунок 5 – Спектральная диаграмма АИМ сигнала при синусоидальном модулирующем сигнале
При отсутствии перемодуляции боковые составляющие, по крайней мере, в 2 раз меньше своих несущих. Задача восстановления непрерывного сигнала из последовательности его дискретных отсчетов как при АИМ-1, так и АИМ-2 заключается в фильтрации модулирующего сигнала с частотой ω, находящегося в низкочастотной части спектра АИМ сигнала, с помощью ФНЧ, при этом подавляются составляющие высокочастотной части спектра.
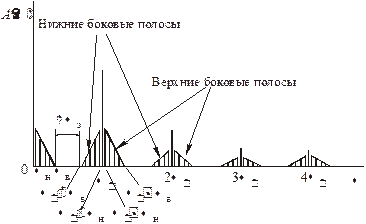
В тех случаях, когда модулирующий сигнал характеризуется спектром с полосой частот от ωн до ωв, спектральная диаграмма АИМ сигнала будет иметь более сложный вид. Теперь вместо отдельных пар боковых колебаний около частот n ω0 (где п = 1, 2, 3,…) будут наблюдаться боковые полосы (рисунок 6), а в низкочастотной части спектра модулированного колебания – спектр модулирующего сигнала. С помощью ФНЧ из такого спектра АИМ сигнала может быть выделена полоса частот модулирующего сигнала. Рассмотрим вопрос о выборе величины частоты дискретизации f 0. Если она выбрана из условия f 0 = 2 F в (ω0 = 2ωв), то, как следует из рисунка 6, нижняя боковая полоса частот, определяемая из условия (ω0 - ωв = 2ωв - ωв = ωв), совпадает с верхней частотой спектра модулирующего сигнала, а для восстановления непрерывного сигнала из последовательности его дискретных отсчетов необходимо использовать идеальный фильтр нижних частот с частотой среза Fср = Fв (ωср = ωв). В реальных системах частоту дискретизации выбирают из условия f 0 > 2 F в, обычно f 0 = (2.3 … 2.4) F в, и, в частности, для дискретизации телефонных сообщений, имеющих диапазон частот 0.3 … 3.4 кГц, величина частоты дискретизации выбрана 8 кГц. При этом образуется защитный промежуток Δ f з (Δωз), позволяющий использовать простые ФНЧ на приеме для восстановления непрерывного сигнала из последовательности его дискретных отсчетов.
Рисунок 6 – Спектральная диаграмма АИМ сигнала при модулирующем сигнале с полосой частот от ωН до ωВ
Если f 0 < 2 F в, то выделение модулирующего сигнала с помощью ФНЧ окажется невозможным, так как в полосу пропускания фильтра попадет часть нижней боковой полосы частот. Таким образом, убеждаемся в необходимости выполнения условия (1), вытекающего из теоремы Котельникова.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.106.38 (0.009 с.) |

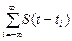 , (4)
, (4)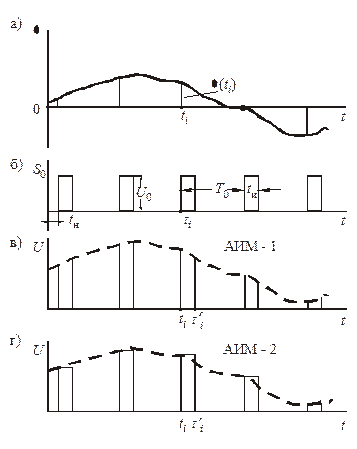
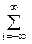 U 0 [1 + m АИМ λ(t)] S (t – ti), (5)
U 0 [1 + m АИМ λ(t)] S (t – ti), (5)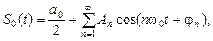 (7)
(7) U 0
U 0  – амплитуда n -й гармоники;
– амплитуда n -й гармоники;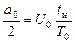 – постоянная составляющая;
– постоянная составляющая;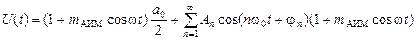
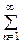 An cos(n ω0 t + φ n) +
An cos(n ω0 t + φ n) +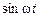 ,(при U = 1 В) то сигнал на выходе модулятора при АИМ-2 определяется соотношением
,(при U = 1 В) то сигнал на выходе модулятора при АИМ-2 определяется соотношением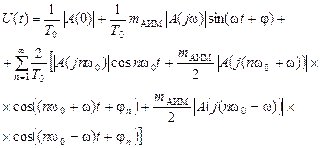 (9)
(9)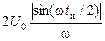 ,
,