
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие сведения из теории колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Колебание системы с конечным числом Степеней свободы В качестве системы с конечным числом степеней свободы рассмотрим невесомую балку с
где
Составляя уравнения, аналогичные равенству (4.1), для каждой массы, получим систему дифференциальных уравнений, общее решение которой указывает на сложный апериодический характер движения масс. Особый интерес представляют такие частные решения указанной системы уравнений, которым соответствуют синхронные равночастотные колебания масс. Такой случай возможен при определенных начальных условиях, если внешняя нагрузка отсутствует, т.е. система совершает свободные колебания. Эти свободные колебания называются собственными или главными. Система с конечным числом степеней свободы в этом случае подобна системе с одной степенью свободы, так как все её точки колеблются с одинаковой частотой
где
Возникающие при этом силы инерции связаны с перемещениями масс и частотой следующей зависимостью:
Подстановка
где Условием ненулевого решения системы (4.4) является характеристическое (вековое) уравнение
Из (4.5) находятся собственные числа Колебания всех масс системы могут происходить с одинаковой частотой и при установившихся вынужденных колебаниях от действия нагрузки меняющейся по гармоническому закону, например:
где Перемещения всех масс следуют этому же закону:
Силы инерции определяются по формуле:
Подстановка (4.8) в (4.1) приводит к следующей системе уравнений:
где
Уравнения (4.9) служат для определения сил инерции при вынужденных колебаниях. Как правило, представляют наибольший интерес амплитудные значения этих сил, в этом случае После определения сил инерции могут быть найдены динамические усилия, в частности моменты
Зависимости (4.9) и (4.11) по форме аналогичны соответствующим зависимостям при расчёте статически неопределимых систем методом сил. Это позволяет назвать такой способ изложения и решения динамической задачи также методом сил. Динамические усилия резко возрастают при совпадении частоты вынужденных колебаний с одной из собственных частот спектра. Если не учитывать силы сопротивления, то наступающее при этом явление резонанса характеризуется неограниченным ростом сил инерции, а значит усилий. Силы сопротивления оказывают набольшее влияние на динамические усилия из-за снижения инерционных сил именно в зоне резонанса. Уже на незначительном удалении от этой зоны их влияние ослабевает. Силы сопротивления в тоже время не сильно влияют на значения частот В качестве примера расчёта рассмотрим раму с одной степенью свободы.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.38.184 (0.007 с.) |

 сосредоточенными массами (Рисунок 4.5). Перемещение
сосредоточенными массами (Рисунок 4.5). Перемещение  любой
любой  -ой массы при действии на балку нагрузки
-ой массы при действии на балку нагрузки  , являющейся функцией времени, можно представить в следующем виде:
, являющейся функцией времени, можно представить в следующем виде: , (4.1)
, (4.1) - сила инерции
- сила инерции  ;
; Рисунок 4.5
Рисунок 4.5
 - перемещение
- перемещение  -ой массе;
-ой массе;
 - перемещение
- перемещение  , и их перемещения следуют гармоническому закону:
, и их перемещения следуют гармоническому закону: , (4.2)
, (4.2) - амплитуда колебаний
- амплитуда колебаний 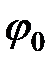 - начальная фаза колебаний.
- начальная фаза колебаний. . (4.3)
. (4.3) , как это следует из (4.3), в (4.1) приводит к системе однородных уравнений при
, как это следует из (4.3), в (4.1) приводит к системе однородных уравнений при  :
: (4.4)
(4.4) .
. (4.5)
(4.5) , частоты
, частоты 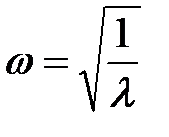 , а из (4.4) – собственные векторы, характеризующие главные (собственные) формы колебаний. Частоты
, а из (4.4) – собственные векторы, характеризующие главные (собственные) формы колебаний. Частоты  , расположенные в порядке возрастания, образуют спектр частот.
, расположенные в порядке возрастания, образуют спектр частот. , (4.6)
, (4.6) - частота вынужденных колебаний.
- частота вынужденных колебаний.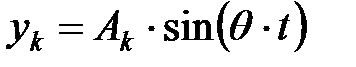 . (4.7)
. (4.7) . (4.8)
. (4.8) (4.9)
(4.9) . (4.10)
. (4.10) в (4.9) представляет собой перемещение
в (4.9) представляет собой перемещение  , возникающие в системе,
, возникающие в системе, . (4.11)
. (4.11) собственных колебаний. Эти обстоятельства позволяют использовать расчёты без учета сил сопротивления при наличии таковых при определении спектра собственных частот свободных колебаний, так и при вычислении динамических усилий в достаточно широком диапазоне частот вынужденных колебаний.
собственных колебаний. Эти обстоятельства позволяют использовать расчёты без учета сил сопротивления при наличии таковых при определении спектра собственных частот свободных колебаний, так и при вычислении динамических усилий в достаточно широком диапазоне частот вынужденных колебаний.


