
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамический расчёт плоской системыСодержание книги
Поиск на нашем сайте
Пример № 4.2
Решение: В направлении возможного смещения массы изображаем силу инерции
Грузовая эпюра от силы инерции:
Определим коэффициенты уравнения:
Подставим в уравнение:
Найдём прогиб рамы в том месте, где находится масса, от действия сил инерции:
Тогда частота свободных колебаний:
Частота вынужденных колебаний:
Т.к. сила инерции зависит от приложенной вибрационной нагрузки, то построим от нее эпюру и уточним значение силы инерции:
Приложим
Для формулы (1) определим значение перемещения от внешней вибрационной нагрузки, чтобы найти силу инерции:
Значение силы инерции:
Уточняем эпюру от силы инерции
Динамический коэффициент:
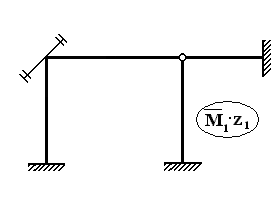
Пример № 4.3 Определение частоты свободных колебаний рамы с одной степенью свободы
В направлении возможного смещения массы изображаем силу инерции
Каноническое уравнение:
Определим коэффициенты уравнения:
Подставим в уравнение:
Найдем прогиб рамы в том месте, где находится масса от действия сил инерции:
Тогда частота свободных колебаний:
Таблица № 1 Уравнение 3-х моментов.
Таблица № 2 Правила перемножения эпюр.
Замечание: если эпюры находятся по разные стороны стержня, то знак в формулах отрицательный (см пример 2) Таблица № 3 - Эпюры изгибающих моментов и реакции опор.
Таблица № 4 - Эпюры изгибающих моментов и реакции опор метода перемещений для сжато-изогнутых стержней.
Таблица № 5 Значения специальных функций для расчетов рам на устойчивость методом перемещений
Библиографический список 1. Анохин Н.Н. Строительная механика в примерах и задачах (Часть I) – М, АВС, 1999г.-334с. 2. Дарков А.В., Шапошников Н.Н. Строительная механика, -М: Высш.шк., 1986г. – 607с. 3. Смирнов А.Ф., Александров А.В. Строительная механика//Динамика и устойчивость сооружений. – М.: Стройиздат, 1981. 4. Саргсян А.Е., Демченко А.Т., Дворячиков Н.В., Джинчвелашвили Г.А. Строительная механика //Основы теории с примерами расчетов: Учебник/ Под ред. А.Е. Саргсяна. – 2-е изд., испр. И доп. – М.:Высшая школа, 2000. 5. Киселев В.А. Строительная механика: Спецкурс // Динамика и устойчивость сооружений. – М.: Стройиздат, 1980. 6. Иванова О.М. Учебное пособие по строительной механике. – Тюмень: ТюмГАСУ, - 2006. 7. Аллахвердов Б.М., Никитин В.М., Яшкин А.Г. Решение задач по устойчивости и динамике сооружений: Методические указания. Ч.2. – СПб.: Петербургский государственный университет путей сообщений, 1996. 8. Клейн Г.К., Рекач В.Г., Розенберг Г.И. Руководство к практическим занятиям по курсу строительной механики. Учебное пособие для втузов. М. «Высшая школа», 1972г.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 826; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.007 с.) |

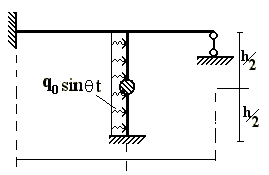 Рисунок 4.19
Рисунок 4.19

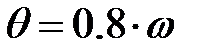
 (Рисунок 4.20) и строим от нее эпюру.
(Рисунок 4.20) и строим от нее эпюру. ,
,


 Рисунок 4.20
Рисунок 4.20
 Рисунок 4.21
Рисунок 4.21
 :
:
 Рисунок 4.22
Рисунок 4.22
 Рисунок 4.23
Рисунок 4.23










 , где
, где - эпюра от силы инерции, построенная в статически определимой раме у которой удалены «лишние» связи
- эпюра от силы инерции, построенная в статически определимой раме у которой удалены «лишние» связи

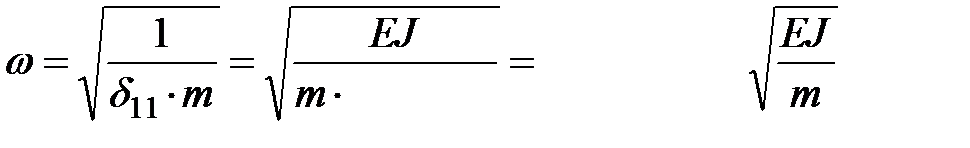 .
. .
. , (4.12), где
, (4.12), где ,
, .
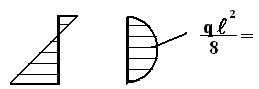
. статически, те как обычную распределенную нагрузку, причем ее максимальное значение. Известно, что
статически, те как обычную распределенную нагрузку, причем ее максимальное значение. Известно, что  , следовательно, загрузим раму
, следовательно, загрузим раму 











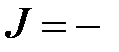

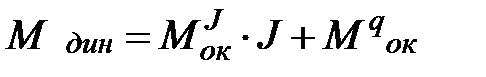

 .
.



 :
:
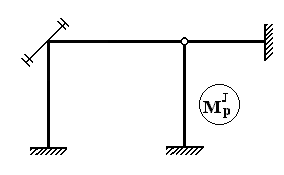


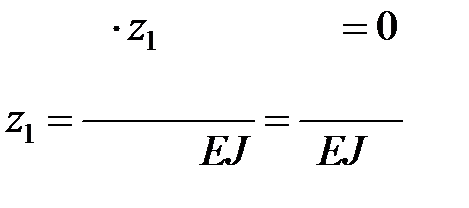


















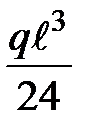




















 ,
, 





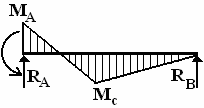

 ;
;
 ;
;


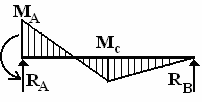















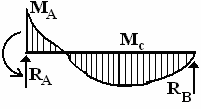


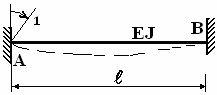

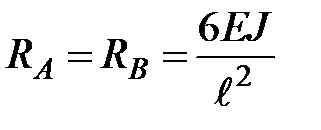 ;
;
 ;
; 


 ;
;




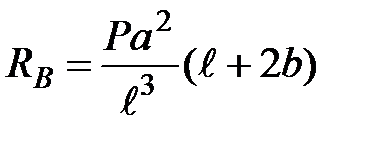 ;
;




 ;
;



 ;
;
 ;
;

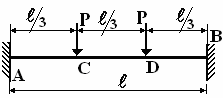

 ;
;



 ;
;
 ;
;












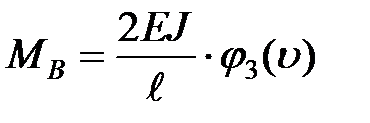




 ;
;






