
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт неразрезной балки с построением объемлющей эпюры
Величины крайних моментов найдем, исходя из внешней нагрузки:
Знак момента отрицательный, т.к. внешняя нагрузка растянула верхние волокна. Для определения величины неизвестных моментов:
где Т.к. нам неизвестны моменты с номерами 1 и 2, то будем иметь следующую систему:
Учитывая, что Найдём недостающие фиктивные реакции, пользуясь таблицей №1 Приложения, при этом заметим, что для пролёта № 2, табличные значения фиктивных реакций:
Подставим их в систему, учитывая, что при данном нагружении
Построим эпюры, по правилу знаков, полученные отрицательные моменты откладываем сверху от базовой линии.
Построение эпюр проводим следующим образом: сначала строим базовую линию, представляющую собой эпюру от изгибающих моментов, полученных по расчётам, затем к этой прямой «подвешиваем» эпюру изгибающих моментов от заданной нагрузки в этом пролёте, как в балке на двух опорах (подвес).
Середина первого пролёта: Поперечные силы.
и для линейных эпюр:
Т.к. мы не определяли опорные реакции, то необходимо сделать проверку правильности расчета, снимем показания «скачков» с эпюры поперечных сил (фактически значения опорных реакций и внешних сосредоточенных сил), двигаясь слева направо, и «соберём» значение распределенной нагрузки в равнодействующую. Давление внешней нагрузки должно быть равно суммарной опорной реакции.
При подборе поперечных сечений неразрезных балок, как и всяких балок, размеры сечений определяются главным образом изгибающими моментами, поэтому вычисляются их наибольшее значение. Если кроме постоянной нагрузки на балку будут действовать различные временные нагрузки, которые могут находиться на ней как совместно, так и раздельно в различных сочетаниях, то необходимо для каждого сечения балки подобрать такое сочетание нагрузок, при котором появлялся бы наибольший изгибающий момент. Мы считали временную нагрузку в пределах одного пролёта несмещаемой и действующей на одновременно на всём пролёте, следовательно можем определить наибольшее расчётное значение изгибающих моментов в каждом сечении, для этого строим объемлющую эпюру или эпюру огибающих моментов. Составим выражения наибольших по абсолютной величине значений положительных и отрицательных изгибающих моментов по формулам:
|
||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.169 (0.007 с.) |
 Врезаем приставные опоры в балку, отбрасывая внутренний момент и заменяя его наперед неизвестными моментами. Нумерацию моментов производим слева направо. Пролёты загружаем фиктивными реакциями.
Врезаем приставные опоры в балку, отбрасывая внутренний момент и заменяя его наперед неизвестными моментами. Нумерацию моментов производим слева направо. Пролёты загружаем фиктивными реакциями.

 ,
,  (т.к. у балки нет консоли и соответственно нагрузки справа)
(т.к. у балки нет консоли и соответственно нагрузки справа) , найдём значение фиктивных реакций и составим уравнения 3-х моментов.
, найдём значение фиктивных реакций и составим уравнения 3-х моментов. , (1.3)
, (1.3) ,
, 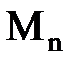 и
и 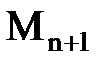 - моменты на опорах
- моменты на опорах  ;
;  - длины левого и правого пролетов;
- длины левого и правого пролетов;  - фиктивная реакция на опоре n от фиктивной нагрузки, действующей на правом и левом пролётах.
- фиктивная реакция на опоре n от фиктивной нагрузки, действующей на правом и левом пролётах. (1,6)
(1,6) ,
,  ,
,  и
и  (1.7)
(1.7) и
и  меняются местами, т.к. наша заданная распределённая нагрузка расположена на правой части балки, а в таблице слева. При подстановке значения
меняются местами, т.к. наша заданная распределённая нагрузка расположена на правой части балки, а в таблице слева. При подстановке значения  в формулу необходимо подставлять всю длину пролёта, а не только ту часть, где расположена распределённая нагрузка.
в формулу необходимо подставлять всю длину пролёта, а не только ту часть, где расположена распределённая нагрузка. ,
,  ,
,  ,
,  .
.



 .
.
 Рисунок 1.4
Рисунок 1.4
 , второго
, второго  , третьего
, третьего  . Т.к. все значения получились положительными и, следовательно, величина подвеса больше, то ординаты откладываем снизу.
. Т.к. все значения получились положительными и, следовательно, величина подвеса больше, то ординаты откладываем снизу. для параболических эпюр
для параболических эпюр , где моменты идут с учётом знака отрицательные моменты откладываются сверху от базовой линии.
, где моменты идут с учётом знака отрицательные моменты откладываются сверху от базовой линии.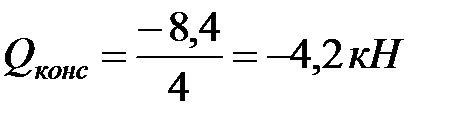 ,
,  ,
,  ,
,  ,
, ,
, .
.

 , где
, где - изгибающий момент от постоянной нагрузки в данном сечении, взятый со своим знаком;
- изгибающий момент от постоянной нагрузки в данном сечении, взятый со своим знаком;  - изгибающие моменты от временной нагрузки, вызывающие в сечении положительный момент;
- изгибающие моменты от временной нагрузки, вызывающие в сечении положительный момент;  - изгибающие моменты от временной нагрузки, вызывающие в сечении отрицательный момент.
- изгибающие моменты от временной нагрузки, вызывающие в сечении отрицательный момент.


