
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция №1 Расчёт многопролетной неразрезной балкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача №1.1 Пример расчёта двухпролётной балки
Величины крайних моментов найдем, исходя из внешней нагрузки:
Знак момента отрицательный, если внешняя нагрузка растянула верхние волокна. Для определения величины момента
Подставим полученные реакции и размеры пролётов в равенство
Значение момента:
Для проверки правильности расчёта, найдём значения поперечных сил, через них определим опорные реакции: Для линейных эпюр параболических эпюр
Задача №1.2 Расчёт балки с построением объемлющей эпюры
Знак момента отрицательный, если внешняя нагрузка растянула верхние волокна. Для определения моментов:
Т.к. нам неизвестны моменты с номерами 0 и 1, то будем иметь следующую систему:
Подставим полученные реакции и размеры пролётов в систему (1.4):
Значения моментов:
Построение объемлющей эпюры 2-го пролёта Загружаем балку временной нагрузкой
Подвес: Фиктивные реакции: Подставим полученные значения в систему (1.5)
Значения моментов: Загружаем 2-ой пролёт
Подвес: Фиктивные реакции: Подставим полученные значения в систему (1.5)
Значения моментов: Загружаем пролёт консоль временной нагрузкой:
Подвес: Фиктивных реакций нет, т.к. загружена только консоль. Подставим значения
Чтобы построить объемлющую эпюру второго пролета, занесем данные моментов в таблицу и определим максимальные и минимальные значения:
Объемлющая эпюра:
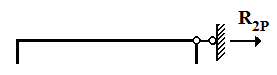
После построения объемлющей эпюры подбирают сечение балки по максимальному значению величины момента, взятому по модулю. Замечание Если жёсткая заделка у балки находится с правой стороны, то основная система будет выглядеть следующим образом (см. следующий пример):
Пример №1.3 Пример №1.4 Лекция №2 Расчёт статически неопределимых рам методом перемещений Задача №2.1 Пример расчёта рамы методом перемещений
1. Число неизвестных методом перемещений:
Подставим полученные коэффициенты в систему (2.1), сократив на
Затем, исправляем единичные эпюры на полученные значения
7. Окончательная эпюра моментов:
8. Эпюра поперечных сил по эпюре моментов:
9. Эпюра продольных усилий (строится методом вырезания узлов).
Задача № 2.2 Пример №2.3 расчёта рамы методом перемещений
Таким образом, имеем следующую задачу:
1. Число неизвестных методом перемещений:
3. Единичные эпюры от
4. Грузовая эпюра от внешней нагрузки:
5. Каноническая система метода перемещений для определения фактических значений
Найдем коэффициенты канонической системы:
Подставим полученные коэффициенты в систему, сократив на
Чтобы получить одинаковые коэффициенты, например при
Сложим равенства и получим значения неизвестных:
6. Исправим единичные эпюры на фактические значения
7. Окончательная эпюра моментов:
8. Эпюра поперечных сил:
Для параболических эпюр моменты идут с учётом знака отрицательные моменты вверху:
9. Эпюра продольных усилий (строится методом вырезания узлов)
Пример № 3.1
Т.к. силы приложены вдоль стержней, то грузовая эпюра будет нулевой, а соответствующие ей грузовые слагаемые:
для более сложных рам определитель будет более высокого порядка.
Значение коэффициентов определителя найдем путём вырезания узлов, как в обычном методе перемещений. Данные для коэффициентов берём из Рисунков 3.4 и 3.5, методом вырезания узлов.
Подставим полученные коэффициенты в определитель (3.2) и вынесем общий множитель 0,5 EJ, тогда
выразим параметры
за единицу измерения примем стержень №2, тогда Равенство (3.4) примет вид:
Решим его численно методом подбора, занося данные в таблицу:
Так как искомое решение находится между полученными значениями, а промежуточных параметров V в таблице функций нет, решение необходимо уточнить. Воспользуемся графической интерпретацией.
Из подобия треугольников: Найдём значение критической силы по формуле Эйлера: (в формулу подставляем длину того стержня, который брали за единицу измерения)
Пример №3.2
Найти значение критической силы. Решаем задачу методом перемещений
Выразим параметры стержней друг через друга
Обозначим Найдём коэффициенты определителя, построив единичные эпюры в основной системе (Рисунок 3.7) от
Тогда определитель устойчивости (3.2) примет вид:
Чтобы упростить равенство, умножим его на
Решим полученное уравнение численно, методом подбора (как в предыдущей задаче):
Как видно из расчёта, функции входящие в равенство не линейные, например сравните значения при
Значение критической силы найдем по формуле Эйлера:
Задача №3.3
Решаем задачу методом перемещений.
Число неизвестных методом перемещений:
Т.к. в раме два жёстких узла, то
Рисунок 3.10 Чтобы решение канонической системы было ненулевым запишем определитель устойчивости Т.к. нагружение рамы простое, т.е.
Найдем коэффициенты определителя, построив единичные эпюры в основной системе (Рисунок 3.10).
Найдём коэффициенты определителя вырезая узлы из единичных эпюр:
Тогда определитель устойчивости примет вид:
Решим уравнение численно:
Значение критической силы найдем по формуле Эйлера:
Лекция № 4 Степеней свободы В качестве системы с конечным числом степеней свободы рассмотрим невесомую балку с
где
Составляя уравнения, аналогичные равенству (4.1), для каждой массы, получим систему дифференциальных уравнений, общее решение которой указывает на сложный апериодический характер движения масс. Особый интерес представляют такие частные решения указанной системы уравнений, которым соответствуют синхронные равночастотные колебания масс. Такой случай возможен при определенных начальных условиях, если внешняя нагрузка отсутствует, т.е. система совершает свободные колебания. Эти свободные колебания называются собственными или главными. Система с конечным числом степеней свободы в этом случае подобна системе с одной степенью свободы, так как все её точки колеблются с одинаковой частотой
где
Возникающие при этом силы инерции связаны с перемещениями масс и частотой следующей зависимостью:
Подстановка
где Условием ненулевого решения системы (4.4) является характеристическое (вековое) уравнение
Из (4.5) находятся собственные числа Колебания всех масс системы могут происходить с одинаковой частотой и при установившихся вынужденных колебаниях от действия нагрузки меняющейся по гармоническому закону, например:
где Перемещения всех масс следуют этому же закону:
Силы инерции определяются по формуле:
Подстановка (4.8) в (4.1) приводит к следующей системе уравнений:
где
Уравнения (4.9) служат для определения сил инерции при вынужденных колебаниях. Как правило, представляют наибольший интерес амплитудные значения этих сил, в этом случае После определения сил инерции могут быть найдены динамические усилия, в частности моменты
Зависимости (4.9) и (4.11) по форме аналогичны соответствующим зависимостям при расчёте статически неопределимых систем методом сил. Это позволяет назвать такой способ изложения и решения динамической задачи также методом сил. Динамические усилия резко возрастают при совпадении частоты вынужденных колебаний с одной из собственных частот спектра. Если не учитывать силы сопротивления, то наступающее при этом явление резонанса характеризуется неограниченным ростом сил инерции, а значит усилий. Силы сопротивления оказывают набольшее влияние на дин
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.250 (0.017 с.) |

 Врезаем приставные опоры в балку, отбрасывая внутренний момент и заменяя его наперед неизвестными моментами. Нумерацию моментов производим слева направо. Пролёты загружаем фиктивными реакциями.
Врезаем приставные опоры в балку, отбрасывая внутренний момент и заменяя его наперед неизвестными моментами. Нумерацию моментов производим слева направо. Пролёты загружаем фиктивными реакциями.


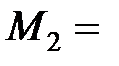
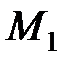 найдём значение фиктивных реакций и составим уравнения 3-х моментов.
найдём значение фиктивных реакций и составим уравнения 3-х моментов.




 ,
, ,
,

 и
и  берутся с учётом знака, если момент растягивает верхние волокна, то знак минус, нижние «плюс».
берутся с учётом знака, если момент растягивает верхние волокна, то знак минус, нижние «плюс».


 , найдём значение фиктивных реакций и составим уравнения 3-х моментов:
, найдём значение фиктивных реакций и составим уравнения 3-х моментов: , (1.3)
, (1.3) (1.4)
(1.4)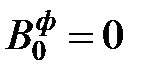 , т.к. нет нагрузки, а точнее нет пролёта,
, т.к. нет нагрузки, а точнее нет пролёта, 


 (1.5)
(1.5)



 , начиная с первого пролёта.
, начиная с первого пролёта.





 в систему (1.5)
в систему (1.5)
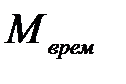





 , где
, где  - число жестких узлов рамы, не связанных с опорами,
- число жестких узлов рамы, не связанных с опорами,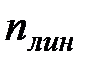 - число степеней свободы условно- шарнирной схемы, т.е. рамы у которой во все узлы врезаны шарниры, в том числе и опорные.
- число степеней свободы условно- шарнирной схемы, т.е. рамы у которой во все узлы врезаны шарниры, в том числе и опорные.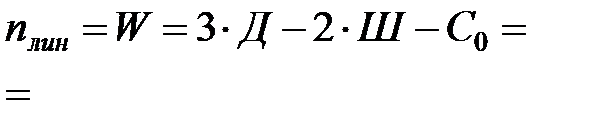 (количество опорных стержней, которые необходимо добавить условно шарнирной схеме, чтобы она стала неподвижной)
(количество опорных стержней, которые необходимо добавить условно шарнирной схеме, чтобы она стала неподвижной)







 :
: (2.1)
(2.1) - реакция, возникающая в заделке с номером
- реакция, возникающая в заделке с номером  , снятая с единичной эпюры Мj,
, снятая с единичной эпюры Мj,  - реакция, возникающая в заделке с номером
- реакция, возникающая в заделке с номером  , снятая с грузовой эпюры
, снятая с грузовой эпюры  .
.










 ,
, 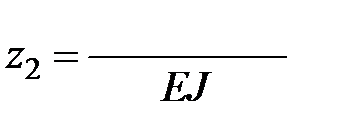
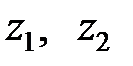 .
.
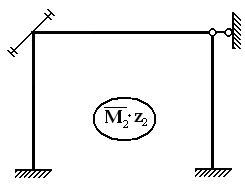
 .
.
 , где
, где  - угол наклона эпюры моментов к стержню, при этом знак «плюс», если поворот стержня к эпюре происходит по часовой стрелке на угол меньше
- угол наклона эпюры моментов к стержню, при этом знак «плюс», если поворот стержня к эпюре происходит по часовой стрелке на угол меньше  .
.










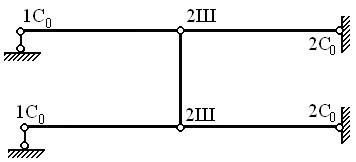
 Дисков пять, одиночных шарниров внутри рамы четыре (шарнир соединяющий три диска двойной), опорных стержней шесть (шарнирно-подвижные опоры по одному, неподвижные опоры по два).
Дисков пять, одиночных шарниров внутри рамы четыре (шарнир соединяющий три диска двойной), опорных стержней шесть (шарнирно-подвижные опоры по одному, неподвижные опоры по два).






 Под распределённой нагрузкой:
Под распределённой нагрузкой:


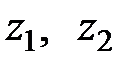 :
:


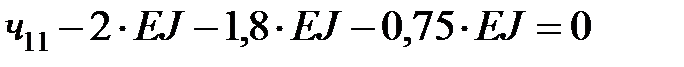 ,
,

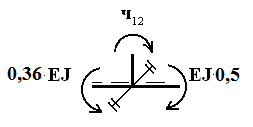
 ,
,













 , умножим второе равенство на 32,5 и перенесём грузовые слагаемые вправо:
, умножим второе равенство на 32,5 и перенесём грузовые слагаемые вправо:
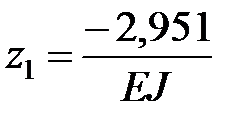 ,
,  .
.

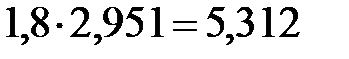




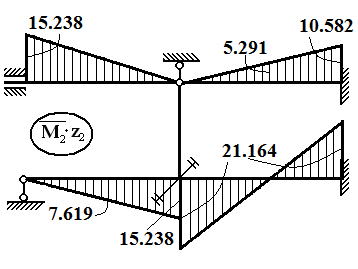
 Моменты изгибающие:
Моменты изгибающие:
 5,312+15,312-7,5=13,05
21,164-5,902=15,262
21,164-2,951=18,213
10,582+18=28,582
9-5,921=3,709.
Для проверки посмотрим равновесие узла:
5,312+15,312-7,5=13,05
21,164-5,902=15,262
21,164-2,951=18,213
10,582+18=28,582
9-5,921=3,709.
Для проверки посмотрим равновесие узла:


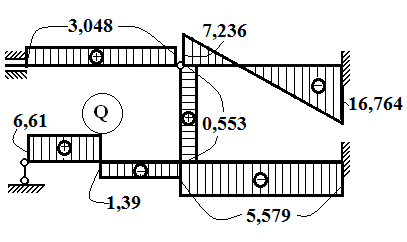
 Рассмотрим расчёт поперечных сил по участкам.
Для линейных эпюр:
Рассмотрим расчёт поперечных сил по участкам.
Для линейных эпюр:
 , где
, где 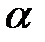 - угол наклона эпюры к стержню.
- угол наклона эпюры к стержню.
 ;
;  ;
; ;
;  ;
;  .
. , где
, где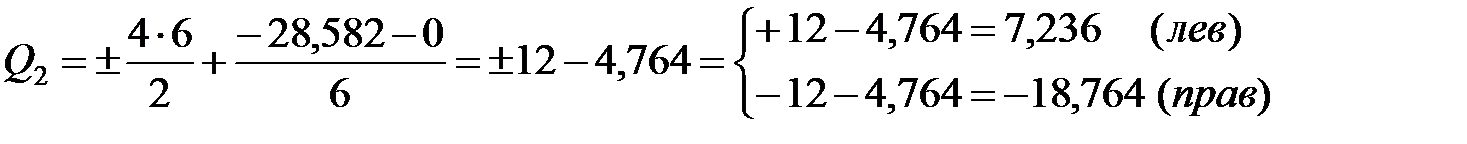


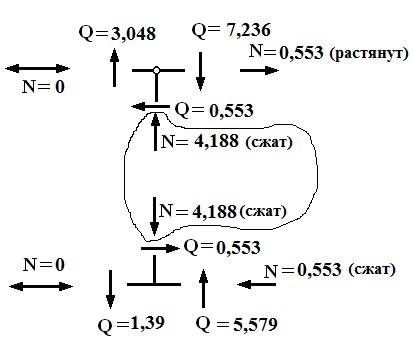
 Рисунок 3.2
Рисунок 3.2
 , схема рамы на Рисунке 3.2.
Найти значение критической силы
, схема рамы на Рисунке 3.2.
Найти значение критической силы
 Решение:
Выберем основную систему метода перемещений
Решение:
Выберем основную систему метода перемещений  , а стержни вдоль которых приложены силы пронумеруем.
, а стержни вдоль которых приложены силы пронумеруем.
 . Построим единичные эпюры. Стержни 1 и 2 являются сжато изогнутыми и эпюры на них строятся по специальным таблицам для расчёта на устойчивость методом перемещений (таблица №4 Приложения). Они носят криволинейных характер и ординаты зависят от параметра влияния продольных сил. В остальных стержнях по таблице №3 Приложения.
. Построим единичные эпюры. Стержни 1 и 2 являются сжато изогнутыми и эпюры на них строятся по специальным таблицам для расчёта на устойчивость методом перемещений (таблица №4 Приложения). Они носят криволинейных характер и ординаты зависят от параметра влияния продольных сил. В остальных стержнях по таблице №3 Приложения. Рисунок 3.3
Рисунок 3.3
 (3.1)
Система уравнений (3.1) является однородной, необходимо найти
(3.1)
Система уравнений (3.1) является однородной, необходимо найти  и
и  , что возможно только при условии линейной зависимости уравнений. Математически это означает, что определитель составленный из коэффициентов равен нулю.
, что возможно только при условии линейной зависимости уравнений. Математически это означает, что определитель составленный из коэффициентов равен нулю.
 или
или (3.2)
(3.2) Рисунок 3.4
Рисунок 3.4
 в основной системе (Рисунок 3.3) получаем схему Рисунка 3.4.
Значения функций
в основной системе (Рисунок 3.3) получаем схему Рисунка 3.4.
Значения функций  определяется численно методом подбора по таблице №5 Приложения.
определяется численно методом подбора по таблице №5 Приложения.
 Рисунок 3.5
Рисунок 3.5
 (Рисунок 3.5), построенная в основной системе (Рисунок 3.3).
(Рисунок 3.5), построенная в основной системе (Рисунок 3.3).










 , (3.4)
, (3.4) и
и  через общий параметр
через общий параметр  , тогда учитывая, что
, тогда учитывая, что  , то для заданных стержней:
, то для заданных стержней: ,
, 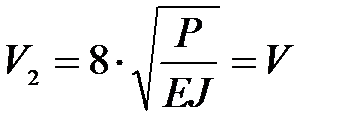
 .
.
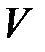

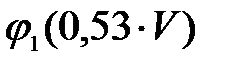




 , значение параметра:
, значение параметра: 
 .
. Рисунок 3.6
Рисунок 3.6


 ,
, 
 Рисунок 3.7
Рисунок 3.7

 Стержни, вдоль которых приложены силы, будут иметь криволинейные эпюры. А т.к. эти силы разные, то необходимо стержни пронумеровать.
Стержни, вдоль которых приложены силы, будут иметь криволинейные эпюры. А т.к. эти силы разные, то необходимо стержни пронумеровать.
 , то
, то 

 , тогда
, тогда 
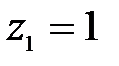 и
и 


















 и
и  они практически одинаковы. Однако значение определителя при
они практически одинаковы. Однако значение определителя при  выпадает из этого диапазона, поэтому по двум далеко отстоящим значениям параметра
выпадает из этого диапазона, поэтому по двум далеко отстоящим значениям параметра  интерполировать решение нельзя.
интерполировать решение нельзя.

 Рисунок 3.8
Рисунок 3.8


 ,
,

 Рисунок 3.9
Рисунок 3.9
 Следовательно
Следовательно  (полученная рама не может двигаться).
(полученная рама не может двигаться).
 .
.
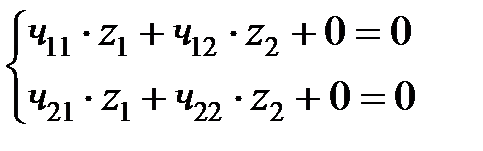
 .
. , то выразим параметры стержней друг через друга
, то выразим параметры стержней друг через друга 











 сосредоточенными массами (Рисунок 4.5). Перемещение
сосредоточенными массами (Рисунок 4.5). Перемещение  любой
любой  -ой массы при действии на балку нагрузки
-ой массы при действии на балку нагрузки  , являющейся функцией времени, можно представить в следующем виде:
, являющейся функцией времени, можно представить в следующем виде: , (4.1)
, (4.1) - сила инерции
- сила инерции  ;
; Рисунок 4.5
Рисунок 4.5
 - перемещение
- перемещение  -ой массе;
-ой массе;
 - перемещение
- перемещение  , и их перемещения следуют гармоническому закону:
, и их перемещения следуют гармоническому закону: , (4.2)
, (4.2) - амплитуда колебаний
- амплитуда колебаний 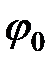 - начальная фаза колебаний.
- начальная фаза колебаний. . (4.3)
. (4.3) , как это следует из (4.3), в (4.1) приводит к системе однородных уравнений при
, как это следует из (4.3), в (4.1) приводит к системе однородных уравнений при  :
: (4.4)
(4.4) .
. (4.5)
(4.5) , частоты
, частоты 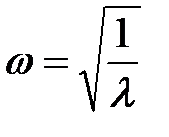 , а из (4.4) – собственные векторы, характеризующие главные (собственные) формы колебаний. Частоты
, а из (4.4) – собственные векторы, характеризующие главные (собственные) формы колебаний. Частоты  , расположенные в порядке возрастания, образуют спектр частот.
, расположенные в порядке возрастания, образуют спектр частот. , (4.6)
, (4.6) - частота вынужденных колебаний.
- частота вынужденных колебаний.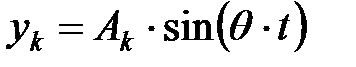 . (4.7)
. (4.7) . (4.8)
. (4.8) (4.9)
(4.9) . (4.10)
. (4.10) в (4.9) представляет собой перемещение
в (4.9) представляет собой перемещение  , возникающие в системе,
, возникающие в системе, . (4.11)
. (4.11)


