
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт на временную нагрузкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Загружаем заданной временной нагрузкой: Загружаем временной нагрузкой консольную часть балки (Рисунок 1.5).
Изгибающий момент консоли:
Система примет вид:
Изобразим полученные результаты на чертеже (Рисунок 1.5), отрицательные моменты вверху базовой линии. Середины пролётов, как средние линии обратных трапеций:
Загружаем первый пролёт (Рисунок 1.6):
Так как загружен 1-й пролёт, то
Подвес на первом пролёте: тогда середины пролётов:
Загружаем временной нагрузкой второй пролёт (Рисунок 1.7):
Т.к. в системе (1.7) фиктивные реакции идут с коэффициентом 6, то
Подвес на втором пролёте определим середины пролётов.
Загружаем временной нагрузкой третий пролёт
Загружаем временной нагрузкой третий пролёт (Рисунок 1.8):
Подвес на третьем пролёте определим середины пролётов.
Составим выражения наибольших по абсолютной величине значений положительных и отрицательных изгибающих моментов по формулам:
Данные возьмём с Рисунков 1.4-1.8 и занесём их в таблицу:
Например, середина 1-го пролёта:
Соотнесём полученные значения на эпюру (Рисунок 1.9):
Лекция №2 Расчёт статически неопределимых рам методом перемещений
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.145.219 (0.01 с.) |

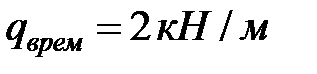 , последовательно все пролёты и консоль.
, последовательно все пролёты и консоль. Рисунок 1.5
Рисунок 1.5
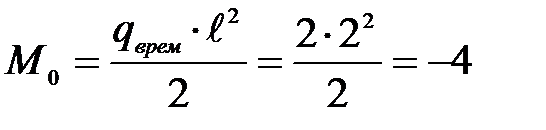 , так как остальные пролёты не загружены, то фиктивные реакции в системе (1.7) равны 0.
, так как остальные пролёты не загружены, то фиктивные реакции в системе (1.7) равны 0.
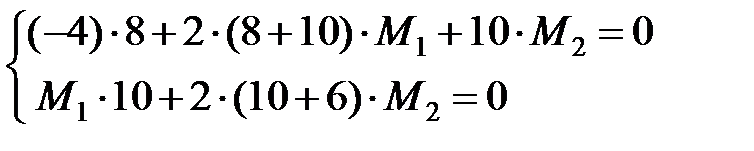 ;
; ;
; .
. (сверху, т.к. левое значение момента больше),
(сверху, т.к. левое значение момента больше), (снизу, т.к. левое значение момента больше),
(снизу, т.к. левое значение момента больше),
 Рисунок 1.6
Рисунок 1.6
 , остальные фиктивные реакции равны нулю и система (1.7) примет вид:
, остальные фиктивные реакции равны нулю и система (1.7) примет вид:
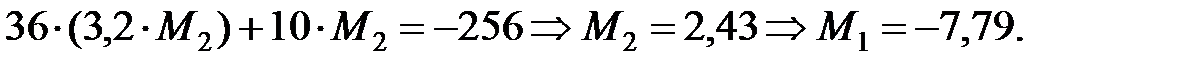
 ,
,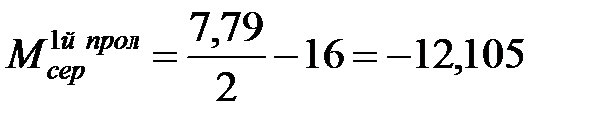 (снизу, т.к. величина подвеса больше),
(снизу, т.к. величина подвеса больше), (сверху, т.к. левое значение момента больше),
(сверху, т.к. левое значение момента больше),  (вверху).
(вверху). Рисунок 1.7
Рисунок 1.7
 , остальные фиктивные реакции равны нулю, система (1.7) примет вид:
, остальные фиктивные реакции равны нулю, система (1.7) примет вид: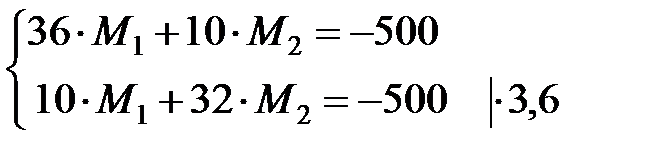

 .
. ,
,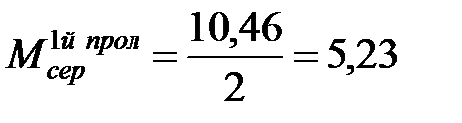 (сверху),
(сверху), (снизу, т.к. величина подвеса больше),
(снизу, т.к. величина подвеса больше), (вверху).
(вверху). , остальные фиктивные реакции равны нулю, система (1.7) примет вид:
, остальные фиктивные реакции равны нулю, система (1.7) примет вид:

 Рисунок1.8
Рисунок1.8
 ,
, (снизу),
(снизу), (сверху, т.к. правый момент больше),
(сверху, т.к. правый момент больше), (снизу, т.к. величина подвеса больше).
(снизу, т.к. величина подвеса больше). , где
, где - изгибающий момент от постоянной нагрузки в данном сечении, взятый со своим знаком;
- изгибающий момент от постоянной нагрузки в данном сечении, взятый со своим знаком; - изгибающие моменты от временной нагрузки, вызывающие в сечении положительный момент;
- изгибающие моменты от временной нагрузки, вызывающие в сечении положительный момент; - изгибающие моменты от временной нагрузки, вызывающие в сечении отрицательный момент.
- изгибающие моменты от временной нагрузки, вызывающие в сечении отрицательный момент. .
. Рисунок 1.9
Рисунок 1.9



