Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт рам методом перемещенийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Число неизвестных методом перемещений:
Грузовая эпюра от внешней нагрузки без учёта неизвестных
Каноническая система метода перемещений для определения фактических значений
Найдем коэффициенты канонической системы:
Подставим полученные коэффициенты в систему (2.1), сократив на
Умножим единичные эпюры на фактические значения
Окончательная эпюра моментов:
Эпюра поперечных сил:
Эпюра продольных усилий (строится методом вырезания узлов)
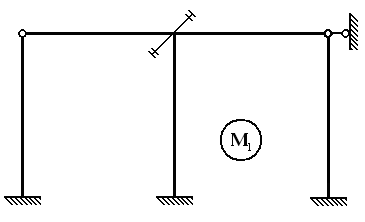
Пример №2.3 расчёта рамы методом перемещений
Таким образом, имеем следующую задачу:
1. Число неизвестных методом перемещений:
3. Единичные эпюры от
4. Грузовая эпюра от внешней нагрузки:
5. Каноническая система метода перемещений для определения фактических значений
Найдем коэффициенты канонической системы:
Подставим полученные коэффициенты в систему, сократив на
Чтобы получить одинаковые коэффициенты, например при
Сложим равенства и получим значения неизвестных:
6. Исправим единичные эпюры на фактические значения
7. Окончательная эпюра моментов:
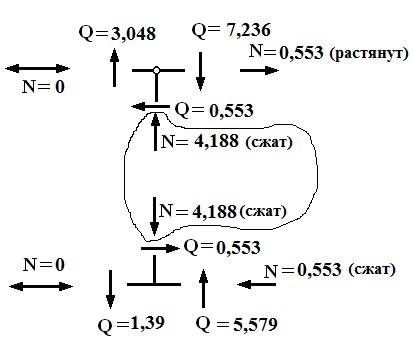
8. Эпюра поперечных сил:
Для параболических эпюр моменты идут с учётом знака отрицательные моменты вверху:
9. Эпюра продольных усилий (строится методом вырезания узлов)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 931; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.70 (0.009 с.) |


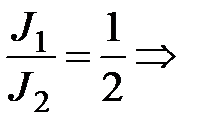
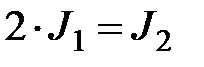
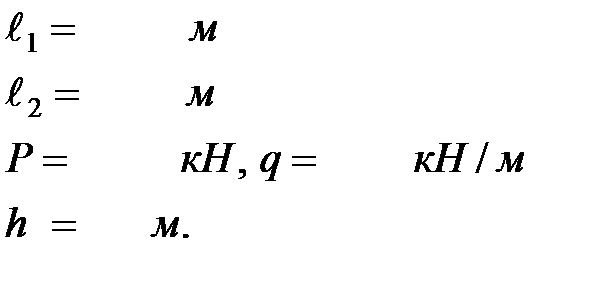
 , где
, где - число жёстких узлов рамы, не связанных с опорами,
- число жёстких узлов рамы, не связанных с опорами,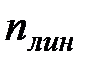 - число степеней свободы условно- шарнирной схемы, т.е. рамы у которой во все узлы врезаны шарниры, в том числе и опорные.
- число степеней свободы условно- шарнирной схемы, т.е. рамы у которой во все узлы врезаны шарниры, в том числе и опорные.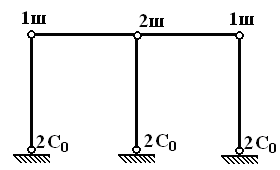
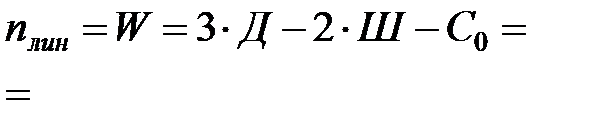 (количество опорных стержней, которые необходимо добавить условно шарнирной схеме, чтобы она стала неподвижной)
(количество опорных стержней, которые необходимо добавить условно шарнирной схеме, чтобы она стала неподвижной)




 и
и 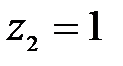 :
:
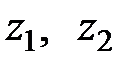 :
: (2.1)
(2.1)
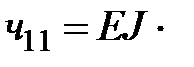











 ,
, 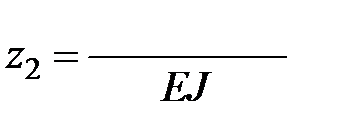 .
.

 Статическая проверка (равновесие жёсткого узла)
Статическая проверка (равновесие жёсткого узла)
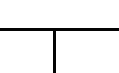

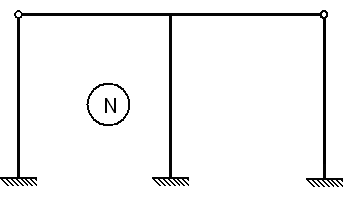






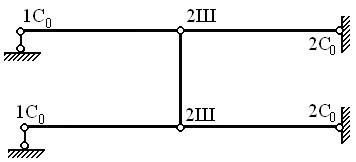
 Дисков пять, одиночных шарниров внутри рамы четыре (шарнир соединяющий три диска двойной), опорных стержней шесть (шарнирно-подвижные опоры по одному, неподвижные опоры по два).
Дисков пять, одиночных шарниров внутри рамы четыре (шарнир соединяющий три диска двойной), опорных стержней шесть (шарнирно-подвижные опоры по одному, неподвижные опоры по два).






 Под распределённой нагрузкой:
Под распределённой нагрузкой:




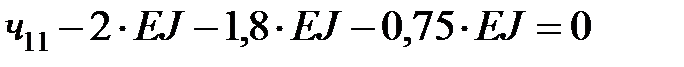 ,
,

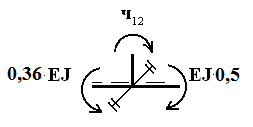
 ,
,













 , умножим второе равенство на 32,5 и перенесём грузовые слагаемые вправо:
, умножим второе равенство на 32,5 и перенесём грузовые слагаемые вправо:
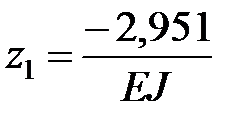 ,
,  .
.

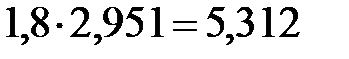




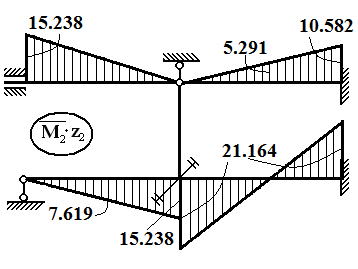
 Моменты изгибающие:
Моменты изгибающие:
 5,312+15,312-7,5=13,05
21,164-5,902=15,262
21,164-2,951=18,213
10,582+18=28,582
9-5,921=3,709.
Для проверки посмотрим равновесие узла:
5,312+15,312-7,5=13,05
21,164-5,902=15,262
21,164-2,951=18,213
10,582+18=28,582
9-5,921=3,709.
Для проверки посмотрим равновесие узла:


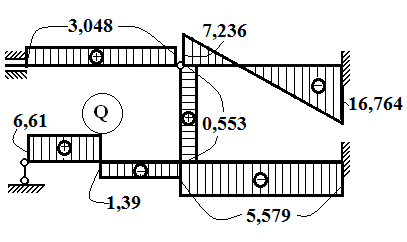
 Рассмотрим расчёт поперечных сил по участкам.
Для линейных эпюр:
Рассмотрим расчёт поперечных сил по участкам.
Для линейных эпюр:
 , где
, где 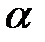 - угол наклона эпюры к стержню.
- угол наклона эпюры к стержню.
 ;
;  ;
; ;
;  ;
;  .
. , где
, где