
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамический расчёт рамы с одной степенью свободыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример №4.1 Построение динамической эпюры Дано: Для рамы (Рисунок 4.6)
1). Методом перемещений строим эпюру МJ1 Число неизвестных:
(один жёсткий узел) (см. Рисунок 4.7) Для условно шарнирной схемы:
Основная система: в жёсткий узел вводим дополнительную жёсткую заделку (Рисунок 4.8)
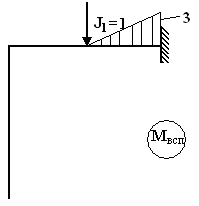
2. Для определения перемещения массы от действия силы инерции строим вспомогательную единичную эпюру от единичной силы инерции J1=1 в статически определимой раме (полученной из заданой с помощью удаления «лишних связей») (Рисунок 4.13), затем перемножаем методом Мора полученную эпюру с окончательной (Рисунок 4.12)
Частота собственных колебаний:
4. Задаем частоту вынужденных колебаний:
5. Т.к. сила инерции зависит от приложенной вибрационной нагрузки, то построим от нее эпюру и уточним значение силы инерции:
где
Приложим Известно, что
3. Эпюру динамических моментов строим по формуле:
4. Находим динамический коэффициент гармонической нагрузки: который показывает в сколько раз её динамическое действие превышает статическое действие её амплитуды. Однако эта формула оказывается недостаточно точной в области, близкой к резонансу, в которой особенно велико влияние затухания. При равенстве частот При
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 , где
, где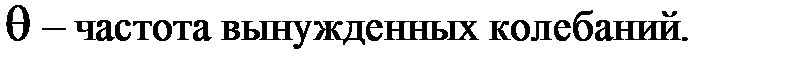










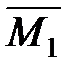 от
от 

 Рисунок 4.10
Рисунок 4.10


 ; неизвестный реактивный момент направляем в сторону
; неизвестный реактивный момент направляем в сторону  , затем с эпюры
, затем с эпюры  снимаем величины моментов в узле «1» (Рисунок 4.9) и находим
снимаем величины моментов в узле «1» (Рисунок 4.9) и находим  .
.


 определим из уравнения равновесия жёсткого узла «1» с грузовой эпюры
определим из уравнения равновесия жёсткого узла «1» с грузовой эпюры  (Рисунок 4.10)
(Рисунок 4.10)

 Рисунок 4.11
Рисунок 4.11
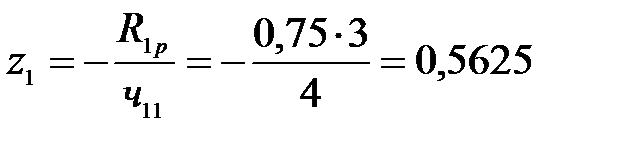 Для построения окончательной эпюры от силы инерции единичную эпюру (Рисунок 4.9) уточним, на полученное фактическое значение
Для построения окончательной эпюры от силы инерции единичную эпюру (Рисунок 4.9) уточним, на полученное фактическое значение  , умножив на него все значения единичной эпюры (Рисунок 4.11).
, умножив на него все значения единичной эпюры (Рисунок 4.11).
 Рисунок 4.12
Рисунок 4.12

 3. Определитель частот для системы с 1 степенью свободы n = 1 из системы (4.5)
3. Определитель частот для системы с 1 степенью свободы n = 1 из системы (4.5)  , где
, где

 МJ1– эпюра в заданной статически неопределимой раме от J1=1, построенная методом перемещений;
М1всп – единичная эпюра в статически определимой системе, полученной из заданной, путём удаления лишних связей.
МJ1– эпюра в заданной статически неопределимой раме от J1=1, построенная методом перемещений;
М1всп – единичная эпюра в статически определимой системе, полученной из заданной, путём удаления лишних связей.

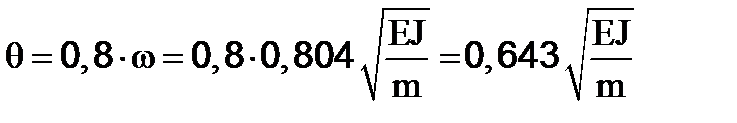
 , (4.12),
, (4.12),
 - перемещение массы от вибрационной нагрузки.
- перемещение массы от вибрационной нагрузки. статически (Рисунок 4.14), те как обычную распределенную нагрузку, причем ее максимальное значение.
статически (Рисунок 4.14), те как обычную распределенную нагрузку, причем ее максимальное значение. , следовательно, загрузим раму
, следовательно, загрузим раму  и построим методом перемещений эпюру в заданной раме.
и построим методом перемещений эпюру в заданной раме. Рисунок 4.14
Рисунок 4.14
 Рисунок 4.15
Рисунок 4.15


 ,
где
,
где  (известна, т.к. основная система, а соответственно единичная эпюра не менялась), грузовой слагаемое только, что получено, тогда:
(известна, т.к. основная система, а соответственно единичная эпюра не менялась), грузовой слагаемое только, что получено, тогда:

 Исправим единичную эпюру (Рисунок 4.9) на полученное значение
Исправим единичную эпюру (Рисунок 4.9) на полученное значение  . Тогда окончательная эпюра от амплитуды динамической нагрузки примет вид (Рисунок 4.16)
. Тогда окончательная эпюра от амплитуды динамической нагрузки примет вид (Рисунок 4.16)
 Рисунок 4.16
Рисунок 4.16

 Тогда инерционная сила из равенства (4.12)
Тогда инерционная сила из равенства (4.12)

 (Рисунок 4.18)
(Рисунок 4.18)
 ,
,
 формула приводит к
формула приводит к  , которые в действительности не могут быть достигнуты.
, которые в действительности не могут быть достигнуты. величина
величина  . Это означает, что колебание возмущающей силы и самой массы происходят в противоположные стороны.
. Это означает, что колебание возмущающей силы и самой массы происходят в противоположные стороны.


