
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степень кинематической неопределимостиСодержание книги
Поиск на нашем сайте
Под степенью кинематической неопределимости принято понимать число основных неизвестных метода перемещений - углов поворота и линейных перемещений жёстких узлов системы. Это число зависит от допущений принятых в методе: 1. Концы стержней, сходящихся в одном жёстком узле, т.е. связанные между собой припайками, поворачиваются на один и тот же угол; 2. Не учитывается влияние 3. Расстояние между узлами при деформации изгиба прямых стержней не изменяются; 4. Углы поворота по малости принимаются равными их тангенсам. Число узловых перемещений определяется числом жёстких узлов, которые независимо могут поворачиваться. При этом за жёстких узел принимается всякий узел, в котором не менее двух стержней соединены между собой припайкой. Число независимых поступательных перемещений узлов не равно числу узлов, которые могут поступательно перемещаться, т.к. на основании 2 и 3 допущений не все поступательные перемещения будут независимы.
систему, введением во все узлы, в том числе опорные, шарниров, считая все стержни абсолютно жёсткими. При этом все статически определимые консоли, если они есть в системе, должны быть предварительно отсечены. Полученная таким образом рама называется условно – шарнирной схемой и она показывает, что узел 1 не может перемещаться по вертикали, т.к. этому
Рассмотрим ещё несколько примеров.
Таким образом, за неизвестные поступательные перемещения принимаем независимые поступательные перемещения, число которых равно количеству дополнительных опорных связей, которое надо добавить условно шарнирной схеме, чтобы она стала неподвижной. В методе перемещений расчёт сводится к построению эпюр для отдельных балок по известным перемещениям и поворотам концов балок. Само решение берётся по стандартным таблицам.
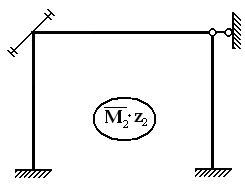
Задача №2.1 Пример расчёта рамы методом перемещений
1. Число неизвестных методом перемещений:
Подставим полученные коэффициенты в систему (2.1), сократив на
Затем, исправляем единичные эпюры на полученные значения
7. Окончательная эпюра моментов:
8. Эпюра поперечных сил по эпюре моментов:
9. Эпюра продольных усилий (строится методом вырезания узлов).
Задача № 2.2
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.117.234 (0.006 с.) |

 на перемещения узлов;
на перемещения узлов;










 , где
, где  - число жестких узлов рамы, не связанных с опорами,
- число жестких узлов рамы, не связанных с опорами,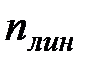 - число степеней свободы условно- шарнирной схемы, т.е. рамы у которой во все узлы врезаны шарниры, в том числе и опорные.
- число степеней свободы условно- шарнирной схемы, т.е. рамы у которой во все узлы врезаны шарниры, в том числе и опорные.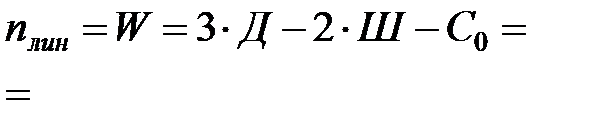 (количество опорных стержней, которые необходимо добавить условно шарнирной схеме, чтобы она стала неподвижной)
(количество опорных стержней, которые необходимо добавить условно шарнирной схеме, чтобы она стала неподвижной)







 :
: (2.1)
(2.1) - реакция, возникающая в заделке с номером
- реакция, возникающая в заделке с номером  , снятая с единичной эпюры Мj,
, снятая с единичной эпюры Мj,  - реакция, возникающая в заделке с номером
- реакция, возникающая в заделке с номером  , снятая с грузовой эпюры
, снятая с грузовой эпюры  .
.






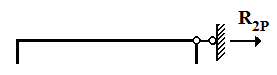




 ,
, 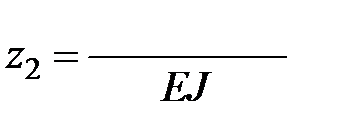
 .
.
 .
.
 , где
, где  - угол наклона эпюры моментов к стержню, при этом знак «плюс», если поворот стержня к эпюре происходит по часовой стрелке на угол меньше
- угол наклона эпюры моментов к стержню, при этом знак «плюс», если поворот стержня к эпюре происходит по часовой стрелке на угол меньше  .
. ,
,

 и
и  берутся с учётом знака, если момент растягивает верхние волокна, то знак минус, нижние «плюс», при этом необходимо стержень повернуть таким образом, чтобы распределённая нагрузка была направлена сверху вниз.
берутся с учётом знака, если момент растягивает верхние волокна, то знак минус, нижние «плюс», при этом необходимо стержень повернуть таким образом, чтобы распределённая нагрузка была направлена сверху вниз.









