
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Циолковского для многоступенчатой ракетыСодержание книги
Поиск на нашем сайте
а) n-ступеней б) в)
17. Канонические уравнения Гамильтона Канонические уравнения:
Система “2S” ДУ 1-го порядка (1) эквивалентна системе “S” ДУ 2-го порядка Канонические уравнения Гамильтона:
Уравнения свободных колебаний системы с одной степенью свободы
Т.к. λ = mg / C
При t=0:
Уравнения вынужденных колебаний системы с одной степенью свободы: силовое возбуждение колебаний Силовое возбуждение колебаний происходит под действием внешней периодической силы P
Подставим в
Если
Уравнения вынужденных колебаний системы с одной степенью свободы: кинематическое возбуждение колебаний Кинематическое возбуждение колебаний происходит под действием внешнего периодического смещения системы.
Подставим в
Свободные колебания системы с одной степенью свободы с затуханием
а) малое сопротивление колебаний
б) сильное сопротивление колебаний
Из (1) получим:
в) n=k Будут апериодические колебания(в которых нельзя выделить полный период колебаний)
Малые свободные колебания систем с 2 степенями свободы. Парциальные частоты
Парциальная система – условная колебательная система с одной степенью свободы, которая соответствует одной из обобщенных координат.
Малые свободные колебания систем с 2 степенями свободы. Нормальные координаты
Из уравнения Лагранжа II рода:
Чтобы найти AB
k – частота собственных колебаний
Нормальные координаты:
Задача Циолковского
S- площадь сопла, p(x)- давление атмосферное, р- давление газа. Из (1): Ракета летит в пустоте:
Из (2):
Поступательное движение твердого тела переменной массы. Уравнение Мещерского Тело переменной массы – тело, масса которого изменяется вследствие отделения или присоединения к телу материальных точек (частиц). Допущения: 1) Рассматриваются только отделение частиц 2) Массы отделяющихся частиц малы 3) Частицы отделяются последовательно 4) Время отделения частиц мало
5) Все точки движутся одинаково, т.к. Уравнение Мещерского. Движение рассматривается вдоль оси х, поэтому пишем скалярные формулы. Из (1):
Формула Циолковского Пренебрежем влиянием силы тяготения. Из
Пусть
Н. у. t=0,
Переменные Лагранжа и Гамильтона; функция Лагранжа и функция Гамильтона Если ввести “S” новых переменных
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.168.68 (0.007 с.) |


 -число циолковского
-число циолковского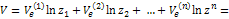

 (1)
(1)

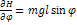




 = 0 | /m
= 0 | /m











 , то наступит резонанс. Если не равны, то резонанса не будет. Резонанс -- явление резкого возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе
, то наступит резонанс. Если не равны, то резонанса не будет. Резонанс -- явление резкого возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе
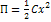

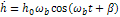





 - десепативная функция Релея (функция рассеивания системы)
- десепативная функция Релея (функция рассеивания системы)

 (1)
(1)
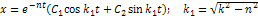

 - частота собственных затухающих колебаний
- частота собственных затухающих колебаний


 – логарифмический декремент (затухание) колебаний. ψ- коэффициент затухания
– логарифмический декремент (затухание) колебаний. ψ- коэффициент затухания

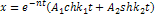





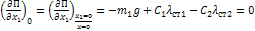 в равновесии
в равновесии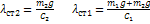



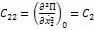





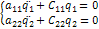
 аij- инерционные коэффициенты
аij- инерционные коэффициенты сij- коэффициенты жесткости
сij- коэффициенты жесткости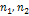 - парциальные частоты
- парциальные частоты


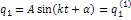






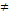 0:
0:
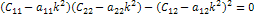



 - нормальные (главные) координаты
- нормальные (главные) координаты




 (1)
(1) - реактивная сила
- реактивная сила -расчет тяги
-расчет тяги
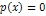
 (2)
(2)


 - эффективная скорость истечения
- эффективная скорость истечения

 - силы тяготения
- силы тяготения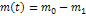 Т.к. процесс отсоединения частиц непрерывный, то
Т.к. процесс отсоединения частиц непрерывный, то  является величиной непрерывной и дифференциальной.
является величиной непрерывной и дифференциальной.
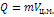 (1). Можно показать, что теорема об изменении количества движения тела переменной массы имеет вид:
(1). Можно показать, что теорема об изменении количества движения тела переменной массы имеет вид:  , U1-абсолютная скорость частицы
, U1-абсолютная скорость частицы


 - относительная скорость
- относительная скорость – уравнение Мещерского
– уравнение Мещерского - реактивная сила
- реактивная сила

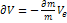

 – эффективная скорость истечения
– эффективная скорость истечения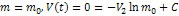


 - формула Циолковского
- формула Циолковского - число Циолковского
- число Циолковского - стартовый вес ракеты
- стартовый вес ракеты
 - формула Циолковского
- формула Циолковского и предположить, что эти зависимости могут быть разрешены относительно обобщенных скоростей
и предположить, что эти зависимости могут быть разрешены относительно обобщенных скоростей  , то система уравнений
, то система уравнений  - форма Лагранжа;
- форма Лагранжа;  - переменные Лагранжа.
- переменные Лагранжа.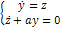 - форма Гамильтона; y, z – переменные Гамильтона
- форма Гамильтона; y, z – переменные Гамильтона - “2S” переменные Гамильтона
- “2S” переменные Гамильтона ;
;  ;
; 
 - функция Гамильтона
- функция Гамильтона - функция Лагранжа (L=T-П);
- функция Лагранжа (L=T-П); - переменные Лагранжа
- переменные Лагранжа


