
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точка, прямая и плоскость на комплексном чертеже.Содержание книги Поиск на нашем сайте
Год. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Конспект лекций ЛЕКЦИЯ 1 ТОЧКА, ПРЯМАЯ И ПЛОСКОСТЬ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ. Методы проецирования.
1.1. Предмет начертательной геометрии 1.2. Из истории начертательной геометрии 1.3. Центральное и параллельное проецирования 1.4. Инвариантные свойства параллельного проецирования 1.5. Ортогональное проецирование 1. 6. Система трех плоскостей проекций. 1. 7. Комплексный чертеж (эпюр Монжа)
Предмет начертательной геометрии
Начертательная геометрия является одной из фундаментальных наук, составляющих основу инженерно-технического образования. Она изучает методы изображений пространственных геометрических фигур на плоскости и способы решения метрических и позиционных задач в пространстве по этим изображениям. Начертательная геометрия используется также при конструировании сложных поверхностей технических форм в железнодорожном, авиационном, морском и речном транспорте. Методы начертательной геометрии позволяют решать многие прикладные задачи специальных инженерных дисциплин (механики, химии, кристаллографии, картографии, инструментоведения и др.) При проектировании и изображении различных транспортных конструкций и сооружений также широко используются методы начертательной геометрии. Конструирование сложных форм поверхностей, автоматизированное проектирование и компьютерная графика находят все большее применение при создании современной транспортной техники. Начертательная геометрия развивает у человека пространственное мышление, без которого немыслимо никакое инженерное творчество. Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записи геометрических предложений и решения задач в начертательной геометрии предлагается использовать геометрический язык, составленный из следующих обозначений и символов. 1. Геометрическая фигура обозначается − Ф. 2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами: A, B, C, D, …,L, M, N, … 1, 2, 3, 4, …, 12, 13, 14, … 3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита: a, b, c, d, …,l, m, n, … Линии уровня обозначаются: h − горизонталь; f − фронталь; p − профильная прямая; Для прямых используются также следующие обозначения: (AB) − прямая, проходящая через точки A и B; [AB) − луч с началом в точке А; [AB] − отрезок прямой, ограниченный точками A и B.
4. Поверхности обозначаются строчными буквами греческого алфавита: α, β, γ, δ, …, ζ, η, λ, … Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например: α (a║b) − плоскость α определяется параллельными прямыми a и b; β (d1d2g α) − поверхность β определяется направляющими d1 и d2, образующей g и плоскостью параллелизма α.
5. Углы обозначаются:
6. Угловая величина (градусная мера) обозначается знаком, который ставится над углом: φº − величина угла φ. Прямой угол отмечается квадратом с точкой внутри.
7. Для плоскостей проекций приняты обозначения: π1 π2 π3, Где π1 − горизонтальная плоскость проекций; π2 − фронтальная плоскость проекций; π3 − профильная плоскость проекций; При замене плоскостей проекций или введении новых плоскостей проекций последние обозначаются π4, π5 и т.д.
8. Оси проекций обозначаются: x,y,z, где x − ось абсцисс; y− ось ординат; z − ось аппликат. Ортогональное проецирование
Ортогональное проецирование является частным случаем параллельного проецирования, когда направление проецирования S перпендикулярно (ортогонально) плоскости проекций S ^ p1 (рис. 1.11).
Рис. 1.11. Ортогональная проекция прямого угла Ортогональное проецирование находит широкое применение в инженерной практике для изображения геометрических фигур на плоскости, т. к. обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием к которым можно отнести: а) простоту графических построений для определения ортогональных проекций точек; б) возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. Указанные преимущества обеспечили широкое применение ортогонального проецирования в технике, в частности для составления машиностроительных чертежей. Для ортогонального проецирования справедливы все девять инвариантных свойств, рассмотренных выше. Кроме того, необходимо отметить еще одно, десятое, инвариантное свойство, которое справедливо только для ортогонального проецирования. 10. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 1.11) На рис. 1.11 показан прямой угол АВD, обе стороны которого параллельны плоскости проекций p1. По инвариантному свойству 9.2 этот угол проецируется на плоскость p1 без искажения, т. е. ÐА1В1D1=90°. Возьмем на проецирующем луче DD1 произвольную точку С, тогда полученный ÐАВС будет прямым, т. к. АВ^ВВ1DD1. Проекцией этого прямого угла АВС, у которого только одна сторона АВ параллельна плоскости проекций p1, будет прямой угол А1В1D1. Говоря о геометрических фигурах и их проекциях необходимо помнить, что проекцией фигуры называют множество проекций всех ее точек.
1.6. Система трех плоскостей проекций. Эпюр Монжа.
Все пространственные геометрические фигуры могут быть ориентированы относительно декартовой прямоугольной системы координатных осей - системы трех взаимно перпендикулярных координатных плоскостей (рис. 1.12).
Рис. 1.12. Изображение системы трех плоскостей проекций Эти координатные плоскости обозначаются: 1. горизонтальная плоскость проекций - p1; 2. фронтальная плоскость проекций - p2; 3. профильная плоскость проекций - p3. Линии пересечения этих плоскостей образуют координатные оси: ось абсцисс – Х; ось ординат – Y; ось аппликат – Z. Точка О пересечения координатных осей принимается за начало координат и обозначается буквой О. Положительными направлениями осей считают: для оси x − влево от начала координат, для оси Y − в сторону зрителя от плоскости p2, для оси z – вверх от плоскости p1; противоположные направления считают отрицательными. Для упрощения дальнейших рассуждений будем рассматривать только часть пространства, расположенную влево от профильной плоскости проекций p3. При таком допущении три координатные плоскости проекций образуют четыре пространственных угла – октанта (в общем случае – 8 октантов). Из рис. 1.12 видно, что ось абсцисс Х делит горизонтальную плоскость проекций p1 на две части: переднюю полу p1 (оси Х и Y) и заднюю полу p1 (оси Х и - Y). Ось абсцисс Х делит фронтальную плоскость проекций p2 также на две части: верхнюю полу p2 (оси Х и Z) и нижнюю полу p2 (оси Х и - Z). Оси ординат Y и аппликат Z делят профильную плоскость проекций p3 на четыре части: 1. верхнюю переднюю полу p3 (оси Y и Z) 2. верхнюю заднюю полу p3 (оси –Y и Z) 3. нижнюю переднюю полу p3 (оси Y и –Z) 4. нижнюю заднюю полу p3 я(оси – Y и –Z)
Для того, чтобы получить плоскую (двухмерную) модель пространственных координатных плоскостей проекций, горизонтальную p1 и профильную p3 плоскости совмещают с фронтальной p2 в том порядке как это показано стрелками на рис. 1.12.
Полученное таким обра- зом совмещение трех плоскос- тей проекций (рис. 1.13) явля- ется плоской моделью систе- мы трех пространственных
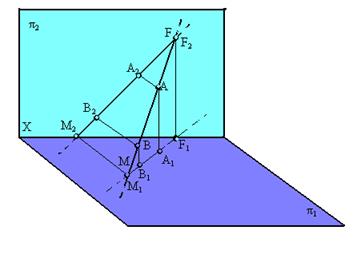
Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций p1, p2 и p3, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром Монжа. Порядок построения эпюры точки, расположенной в первом октанте. На рис. 1.13 изображена пространственная точка А, координаты которой (x, y, z) показывают величины расстояний, на которые точка удалена от плоскостей проекций.
Точки пересечения этих перпендикуляров с плоскостями проекций образуют проекции точки А: А1 – горизонтальную проекцию точки; А2 – фронтальную проекцию точки;
На рис. 1.14 плоскости проекций p1 и p3 совмещены с плоскостью чертежа (с плоскостью проекции p2), а вместе с ними совмещены с плоскостью чертежа и проекции точки А (А1, А2, А3) и таким образом получена плоскостная модель координатных плоскостей проекций и плоскостная модель пространственной точки А – ее эпюра. Положение проекций точки А на эпюре однозначно определяется ее тремя координатами (рис. 1.14). На рис. 1.13 и рис. 1.14 также видно, что на эпюре горизонтальная и фронтальная проекции точки лежат на одном перпендикуляре к оси Х, а также фронтальная и профильная проекции – на одном перпендикуляре к оси Z:
А1А2 ^ Х, А2А3 ^ Z.
Из рис 1.12 видно, что точки, расположенные в различных октантах, имеют определенные знаки координат. В таблице приведены знаки координат точек, расположенных в различных октантах
Таблица знаков координат
Лекция 2
Следы прямой линии Следом прямой линии называется точка пересечения прямой с плоскостью проекций. В системе двух плоскостей проекций p1 и p2 прямая в общем случае имеет два следа (рис. 2.11 а,б): 1. Горизонтальный Н (Н1, Н2); 2. Фронтальный F (F1, F2)
а) б)
Рис. 2.11. Изображение следов прямой линии: а) в пространстве; б) на эпюре
Это точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций. Установим правило нахождения следов прямой.
Для нахождения горизонтального следа прямой необходимо: 1) продолжить фронтальную проекцию прямой а до пересечения с осью Х (получим точку НХ º Н2) 2) восстановить перпендикуляр в точке НХ к оси Х (провести линию связи перпендикулярную к оси Х); 3) продолжить горизонтальную проекцию прямой а до пересечения с перпендикуляром; 4) полученная точка пересечения и будет являться горизонтальным следом прямой а Н º Н1
Для нахождения фронтального следа прямой необходимо: 1) продолжить горизонтальную проекцию прямой а до пересечения с осью Х (точка FXº F1); 2) восстановить перпендикуляр в точке FX к оси Х; 3) продолжить фронтальную проекцию прямой до пересечения с перпендикуляром; 4) полученная точка пересечения Fº F2 является фронтальным следом прямой а
В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическим фигурами будут только те, которые расположены в первом октанте. Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.
2.4.Ортогональная проекция плоскости
На эпюре плоскость может быть задана графически одним из следующих способов, показанных на рис. 2.12.
а) б)
д) е)
ж)
Рис. 2.12. Способы задания плоскости: а − тремя точками не лежащими на одной прямой; б − прямой и точкой вне ее; в − двумя пересекающимися прямыми; г − двумя параллельными прямыми; д, е − плоской фигурой; ж − следами плоскости
2.5. Частные случаи расположения плоскостей в пространстве
Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекции.
Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости.
1. Горизонтально проецирующая плоскость a^p1.
Рис. 2.13. Изображение горизонтально-проецирующей плоскости
Плоскость a, перпендикулярная горизонтальной плоскости проекции p1, называется горизонтально проецирующей (рис. 2.13). Основным свойством горизонтально проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на p1 в прямую линию (горизонтальный след плоскости h0a). Угол b, который составляет горизонтальный след плоскости h0a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций p2. Фронтальный след такой плоскости перпендикулярен оси Х (f0a ^ X).
2. Фронтально проецирующая плоскость b ^ p2. Плоскость b перпендикулярная фронтальной плоскости проекций p2 называется фронтально проецирующей (рис. 2.14).
Рис. 2.14. Изображение фронтально-проецирующей плоскости
Основным свойством фронтально-проецирующей плоскости является то, что любая фигура. Расположенная в этой плоскости, проецируется на p2 в прямую линию (фронтальный след плоскости f0b). Угол a, который составляет фронтальный след плоскости f0b с координатной осью Х, равен углу наклона плоскости b к плоскости проекций p1. Горизонтальный след такой плоскости перпендикулярен оси Х.
Плоскости, параллельные плоскостям проекций (плоскости уровня)
1. Горизонтальная плоскость g÷÷p1.
Плоскость g, параллельная плоскости p1, называется горизонтальной (рис. 2.15).
Рис. 2.15. Изображение плоскости, параллельной горизонтальной плоскости проекций
Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскости проекций в натуральную величину (D А1В1С1=DАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f0g½½Х).
2. Фронтальная плоскость d½½p2.
Плоскость d, параллельная плоскости p2, называется фронтальной. Любая фигура расположенная в такой плоскости. Проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину. Горизонтальный след фронтальной плоскости параллелен оси Х. Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей. Плоскость общего положения
Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций – произвольные, но отличные от 0° и 90°) называется плоскостью общего положения (рис. 2.16.а). На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.
2.6. Следы плоскости
Следом плоскости a называется линия пересечения этой плоскости с плоскостью проекций.
а б
Рис. 2.16. Пример изображения следов плоскости: а) в пространстве; б) на комплексном чертеже
В системе двух плоскостей проекций p1 и p2 плоскость в общем случае имеет два следа: горизонтальный ha0 и фронтальный fa0, которые являются пересечением плоскости a соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.16). Точки пересечения плоскости a с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно Sx, Sy, Sz (рис. 2.16.а). Главные линии плоскости Главными линиями плоскости называют: 1. Горизонталь − прямую, принадлежащую плоскости и параллельную горизонтальной плоскости проекций. 2. Фронталь − прямую, принадлежащую плоскости и параллельную фронтальной плоскости проекций. 3. Линию наибольшего наклона − прямую, принадлежащую плоскости и перпендикулярную к горизонтали или фронтали этой плоскости.
Лекция 3
Лекция 4
МЕТРИЧЕСКИЕ ЗАДАЧИ
4.1. Условие перпендикулярности двух прямых на комплексном чертеже 4.2. Условие перпендикулярности прямой к плоскости 4.3. Условие перпендикулярности плоскостей 4.4. Определение длины отрезка и углов наклона его к плоскостям проекций 4.5. Линия наибольшего наклона (ската)
4.1 Условие перпендикулярности двух прямых на комплексном чертеже Особый интерес с точки зрения решения задач начертательной геометрии представляют перпендикулярные прямые. Из классической Евклидовой геометрии известно следующее свойство перпендикулярности двух прямых: Две прямые перпендикулярны, если угол меду ними составляет 90°. Кроме того, в начертательной геометрии существует еще одно утверждение на эту тему: Две прямые перпендикулярны, если одна из них линия уровня. Для подтверждения этого заключения рассмотрим примеры, приведенные на рис. 4.1. Предположим что необходимо через точку А провести прямую ℓ, пересекающую горизонталь h прямым углом ℓ Так как одна из сторон h прямого угла параллельна плоскости π1, то на эту плоскость прямой угол спроецируется без искажения. Поэтому через горизонтальную проекцию А1 проведем горизонтальную проекцию искомой прямой ℓ1 Если вместо горизонтали будет задана фронталь f, то геометрические построения по проведению прямой ℓ
а) б) Рис. 4.1. Примеры построения перпендикулярных прямых: а) ℓ
4.2. Условие перпендикулярности прямой к плоскости Прямая а перпендикулярна плоскости α, если она перпендикулярна двум пересекающимся прямым b и с этой плоскости.
Если прямые b и с, принадлежащие плоскости α, расположены произвольно относительно плоскостей проекций, то прямые углы между прямой а и прямыми b и с спроецируются на плоскость проекций с искажениями. Для того чтобы эти прямые углы спроецировались в натуральную величину, прямые b и с должны быть параллельны плоскостям проекций, т. е. являться соответственно горизонталью и фронталью плоскости α. Прямая а перпендикулярна плоскости α, если она перпендикулярна пересекающимся горизонтали h и фронтали f этой плоскости. При этом прямые углы между прямой а и прямыми h и f на соответствующие плоскости проекций спроецируются без искажений. Кроме вышесказанного существует теорема:
а) б)
Рис. 4.2. Изображение прямых, перпендикулярных к плоскостям заданным: а) плоскостью фигуры АВС; б) прямыми c, d
Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим проекциям горизонтали h и фронтали f этой плоскости. На рис. 4.2 изображены прямые перпендикулярные плоскостям, заданным различными способами. Если плоскость задана следами, то горизонталью и фронталью плоскости являются ее пересекающиеся следы. Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим пересекающимся следам плоскости (рис. 4.3).
Рис.4.3. Изображение прямой а перпендикулярной к плоскости, заданной следами
4.3. Условие перпендикулярности плоскостей
Плоскости α и β перпендикулярны, если одна плоскость проходит через перпендикуляр другой плоскости. На рис. 4.3 показана прямая а перпендикулярная плоскости α, (следовательно, любая плоскость, проходящая через прямую а, будет перпендикулярна плоскости α. На рис. 4.4 изображены две проецирующие плоскости β и γ и произвольная плоскость δ, следы которой проходят через следы прямой а.
Рис. 4.4. Условие перпендикулярности плоскостей
Рис. 4.5. Условие перпендикулярности плоскостей
4.4. Определение действительной длины отрезка и углов наклона его к плоскостям проекций
Рис. 4.6. Определение углов наклона и натуральной величины отрезков
На рис. 4.6 показаны в аксонометрической проекции отрезок АВ и его горизонтальная проекция А1В1. Проведя прямую ВВ’, параллельную горизонтальной проекции отрезка А1В1, получим прямоугольный треугольник Δ АВВ’. Длина отрезка АВ равна гипотенузе этого треугольника, катетами которого являются горизонтальная проекция отрезка А1В1 и разность координат z точек А и В (Δz = zA- zB). Как известно, угол наклона прямой к плоскости равен углу между этой прямой АВ и ее проекцией на плоскость (А1В1).
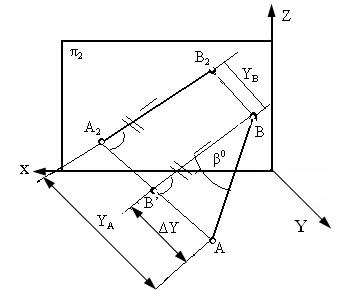
Рис. 4.7. Определение углов наклона и натуральной величины отрезков
Аналогично рассуждая (рис. 4.7), можно показать, что длина отрезка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А2В2 и разность координат Y точек А и В (ΔY =YA- YB). Угол этого треугольника, лежащий против катета ΔY, равен углу наклона отрезка АВ к фронтальной плоскости проекций π2 (угол β°). По аналогии длина отрезка АВ может быть определена и как гипотенуза треугольника, катеты которого профильная проекция отрезка А3В3 и разность координат Х (Δ Х = ХА – ХВ) точек А и В. Угол γ° этого треугольника,
лежащий против катета Δ Х, определяет угол наклона отрезка АВ к профильной плоскости проекций π3. На рис. 4.8 показан пример определения длины отрезка АВ и углов наклона его к плоскостям проекций.
Рис. 4.8. Определение длины отрезка и углов наклона к плоскостям проекций
4.5. Линия наибольшего наклона (ската)
Главным свойством этой линии является то, что она образует с горизонтальной плоскостью проекций π1 угол α°, равный углу наклона плоскости γ к плоскости π1. Это свойство линии наибольшего наклона (ската) используется для определения углов наклона плоскостей к плоскостям проекций.
ЛЕКЦИЯ 5 СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА 5. 1. Необходимость преобразований комплексного чертежа 5.2. Задачи на преобразование комплексного чертежа 5.3. Пути осуществления преобразования комплексного чертежа
5.1. Необходимость преобразований комплексного чертежа. Трудоемкость и, как следствие, точность графического решения задач часто зависят не только от сложности задач, но и от того, какое положение занимают геометрические фигуры, входящие в условие задачи, по отношению к плоскостям проекций. Проецируемая фигура может занимать по отношению к плоскостям проекций произвольное, или частное положение. В первом случае, как правило, получаются проекции, неудобные для решения задач. Решение задачи значительно упрощается, когда мы имеем дело с частным расположением геометрических фигур относительно плоскостей проекций. Наиболее выгодным частным положением проецируемой фигуры при ортогональном проецировании следует считать: 1) положение, перпендикулярное к плоскости проекций – при решении позиционных задач; 2) положение, параллельное плоскости проекций – для решения метрических задач. Таким образом, при решении той или иной задачи бывает целесообразно привести фигуру к частному положению. Переход от общего положения геометрической фигуры к частному можно осуществлять изменением взаимного положения проецируемой фигуры и плоскости проекции. При ортогональном проецировании это может быть достигнуто двумя путями: 1) перемещением в пространстве проецируемой фигуры, по отношению к плоскости проекций. 2) выбором новой плоскости проекций, по отношению к проецируемой фигуре. Первый путь лежит в основе плоскопараллельного перемещения; второй – составляет теоретическую базу способа замены плоскостей проекций.
5.2. Задачи на преобразование комплексного чертежа Все метрические и позиционные задачи можно свести к одной из следующих четырех задач. Задача №1. Преобразовать комплексный чертеж так, чтобы прямая общего положения АВ оказалась параллельной одной из плоскостей проекций т.е. прямой уровня (горизонталь или фронталь) новой системы.
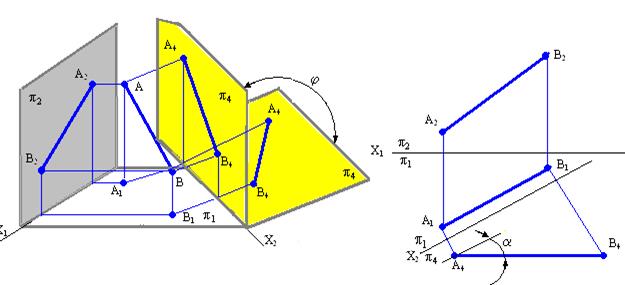 Для решения задачи необходимо заменить плоскость проекций П1, или П2 новой плоскостью проекций П4, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П2 новой плоскостью П4 Для решения задачи необходимо заменить плоскость проекций П1, или П2 новой плоскостью проекций П4, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П2 новой плоскостью П4 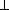 П1 и параллельной прямой АВ. П1 и параллельной прямой АВ. Рассмотрим подробно этапы построения на комплексном чертеже (рис. 5.1), необходимые для решения первой основной задачи на преобразование комплексного чертежа: 1) провести новую ось проекций х14 параллельно А1В1 на произвольном расстоянии от нее; такое положение оси х14 обусловливается тем, что П4 параллельна АВ. В частном случае, если плоскость П4 проведена непосредственно через прямую АВ, ось х14 = А1В1; 2) выбрать на прямой две точки А(А1А2) и В(В1В2); 3) построить проекции точек А и В на плоскости П4; 4) Рис. 5.1. Преобразование прямой общего положения в прямую уровня
прямая А4В4 является проекцией прямой АВ на плоскость П4. Прямая AB в новой системе плоскостей проекций П1/П4 является фронталью, Отрезок [АВ] прямой проецируется на плоскость П4 в истинную величину, т.е. | А4В4 | = | АB |, a- величина угла наклона прямой АВ к плоскости П1.
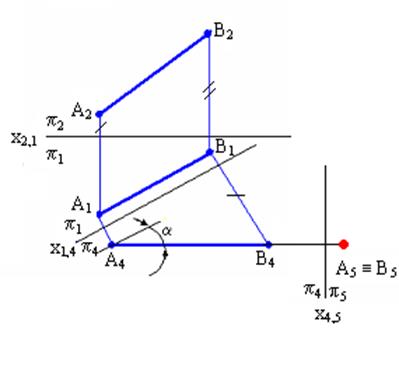 3адача 2. Преобразовать линию общего положения АВ в проецирующую прямую. Решение. 3адача 2. Преобразовать линию общего положения АВ в проецирующую прямую. Решение.
так как АВ // П4 и образует с ней новую систему плоскостей проекций П1/П4. Построения на комплексном чертеже: 1) проводим новую ось проекций х14 // А1В1; 2) построим проекции точек А и В на плоскости П4, взяв координаты точек из плоскости П2. 3) Заменим плоскость П1 на новую П5, которая будет 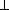 П4 и А4В4. Для этого проводим новую ось проекций х4,5. Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5. Прямая АВ (А5В5) в новой системе плоскостей проекций заняла проецирующее положение и является горизонтально проецирующей. Прямую общего положения преобразовать в проецирующую заменой только одной плоскости проекций нельзя, так как плоскость П5 перпендикулярная прямой, не будет перпендикулярна ни одной из старых плоскостей проекций, и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций. П4 и А4В4. Для этого проводим новую ось проекций х4,5. Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5. Прямая АВ (А5В5) в новой системе плоскостей проекций заняла проецирующее положение и является горизонтально проецирующей. Прямую общего положения преобразовать в проецирующую заменой только одной плоскости проекций нельзя, так как плоскость П5 перпендикулярная прямой, не будет перпендикулярна ни одной из старых плоскостей проекций, и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.
Для того чтобы прямую общего положения преобразовать в проецирующую, необходимо выполнить две последовательные замены плоскостей проекций. Вначале прямую следует преобразовать в линию уровня, а затем линию уровня преобразовать в проецирующую. На рис.5.2 показано преобразование прямой АВ общего положения в горизонтально проецирующую.
Задача №3. Преобразовать комплексный чертеж так, чтобы плоскость общего положения в новой системе плоскостей проекций стала проецирующей (рис. 5.3).
 (АВС). Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости (АВС). Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости  , преобразовать в проецирующую, то плоскость , преобразовать в проецирующую, то плоскость  в новой системе плоскостей проекций станет проецирующей. Проще всего для этой цели воспользоваться линией уровня. в новой системе плоскостей проекций станет проецирующей. Проще всего для этой цели воспользоваться линией уровня.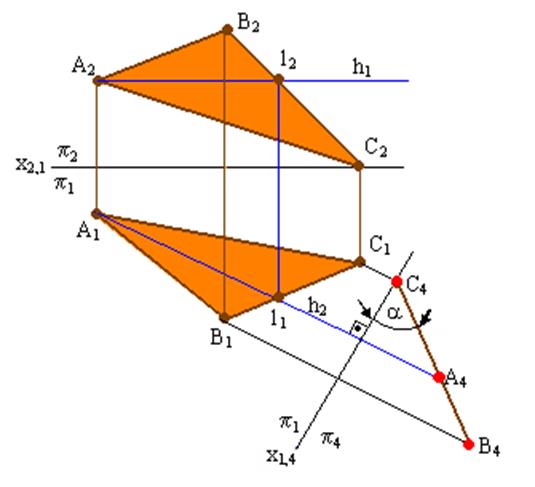
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.014 с.) |

 АВС − угол с вершиной в точке В, а также
АВС − угол с вершиной в точке В, а также  αº,
αº, 


 При этом горизонтальная плоскость проекций p1 вращается вокруг оси Х на 90°, а профильная плос- кость проекций p3 вращается вокруг оси Z также на 90° (на- правление вращения показано на рис. 1.12).
При этом горизонтальная плоскость проекций p1 вращается вокруг оси Х на 90°, а профильная плос- кость проекций p3 вращается вокруг оси Z также на 90° (на- правление вращения показано на рис. 1.12). Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций.
Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций. А3 – профильную проекцию точки.
А3 – профильную проекцию точки.













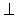 h (рис. 4.1.а).
h (рис. 4.1.а).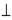 h1. Отметим горизонтальную проекцию точки пересечения прямой и горизонтали N1= ℓ1 ∩ h1. Найдем по принадлежности фронтальную проекцию точки пересечения N2. Точки А2 и N2 определяют фронтальную проекцию искомой прямой ℓ. Две проекции прямой определяют ее положение в пространстве.
h1. Отметим горизонтальную проекцию точки пересечения прямой и горизонтали N1= ℓ1 ∩ h1. Найдем по принадлежности фронтальную проекцию точки пересечения N2. Точки А2 и N2 определяют фронтальную проекцию искомой прямой ℓ. Две проекции прямой определяют ее положение в пространстве.
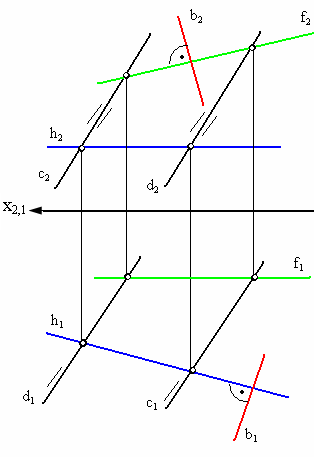 Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция − к фронтальной проекции фронтали этой плоскости.
Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция − к фронтальной проекции фронтали этой плоскости.

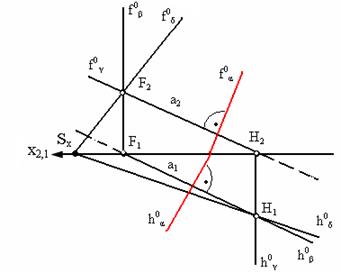
 На рис. 4.5 изображена прямая b, перпендикулярная плоскости Δ АВС, следовательно, любая плоскость, проходящая через прямую b, будет перпендикулярна плоскости Δ АВС.
На рис. 4.5 изображена прямая b, перпендикулярная плоскости Δ АВС, следовательно, любая плоскость, проходящая через прямую b, будет перпендикулярна плоскости Δ АВС.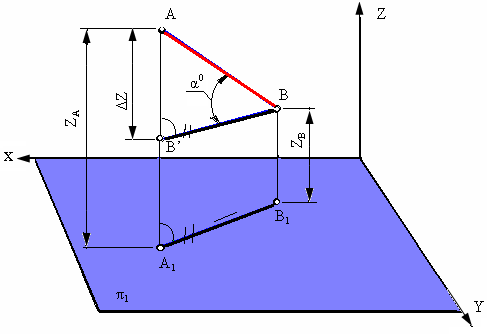
 Следовательно, угол Δ АВВ’, лежащий против катета Δz, равен углу наклона отрезка АВ и горизонтальной плоскости проекций π1 (угол α°).
Следовательно, угол Δ АВВ’, лежащий против катета Δz, равен углу наклона отрезка АВ и горизонтальной плоскости проекций π1 (угол α°).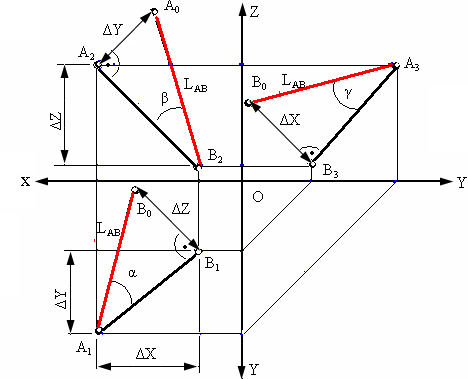
 Линией наибольшего ската плоскости γ называется прямая g, принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f (рис.4.9). На комплексном чертеже горизонтальная проекция линии наибольшего наклона перпендикулярна горизонтальной проекции горизонтали этой плоскости, а фронтальная − фронтальной проекции фронтали.
Линией наибольшего ската плоскости γ называется прямая g, принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f (рис.4.9). На комплексном чертеже горизонтальная проекция линии наибольшего наклона перпендикулярна горизонтальной проекции горизонтали этой плоскости, а фронтальная − фронтальной проекции фронтали.
 На чертеже плоскость
На чертеже плоскость  - величина угла наклона плоскости
- величина угла наклона плоскости 


