
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральное и параллельное проецированиеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Проекцией точки А на плоскость проекций p1 называется точка А1 пересечения проецирующей прямой ℓ с плоскостью проекций p 1, проходящей через точку А, (рис. 1.1):
Проекция любой геометрической фигуры есть множество проекций всех ее точек. Направление проецирующих прямых ℓ и положение плоскостей p1 определяют аппарат проецирования.
Параллельным проецированием называют такое проецирование, при котором все проецирующие прямые параллельны заданному направлению S (рис. 1.3).
При заданном аппарате проецирования каждой точке пространства соответствует одна и только одна точка на плоскости проекций. Одна проекция точки не определяет положения этой точки в пространстве. Действительно, проекции А1 может соответствовать бесчисленное множество точек А’, А’’, …, расположенных на проецирующей прямой ℓ (рис. 1.4).
Для определения положения точки в пространстве при любом аппарате проецирования необходимо иметь две ее проекции, полученных при двух различных направлениях проецирования (или при двух различных центрах проецирования). Так, из рис. 1.5 видно, что две проекции точки А (А1 и А2), полученные при двух направлениях проецирования S1 и S2, определяют единственным образом положение самой точки А в пространстве – как пересечение проецирующих прямых ℓ1 и ℓ2, проведенных из проекций А1 и А2 параллельно направлениям проецирования S1 и S2.
Рис. 1.5. Определение положения точки А в пространстве
1.4. Инвариантные свойства параллельного проецирования
Геометрические фигуры в общем случае проецируются на плоскость проекций с искажением. Проекции не сохраняют линейные и угловые величины оригинала. Характер искажений зависит от положения геометрической фигуры в пространстве, от аппарата проецирования и от положения плоскости проекций. Однако некоторые геометрические свойства фигур остаются неизменными в процессе проецирования. Такие свойства геометрических фигур называются независимыми или инвариантными для данного аппарата проецирования. Рассмотрим основные инвариантные свойства параллельного проецирования.
1. Проекция точки есть точка
Это очевидно из самого определения проекции как точка пересечения проецирующей прямой с плоскостью. 2. Проекция прямой есть прямая (рис. 1.6)
Рис. 1.6. Инвариантные свойства 2, 3, 4
Все проецирующие прямые, проходящие через точки прямой а параллельно направлению проецирования S, образуют проецирующую, или лучевую, плоскость a. Проекция прямой а на плоскость p1 определяется как линия пересечения этой лучевой плоскости a с плоскостью p1, т. е. прямая 3. Если точка К принадлежит прямой а, то и проекция этой точки принадлежит проекции прямой (рис. 1.6) Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек. Если точка К принадлежит прямой а и плоскости a, то и проецирующий луч lК принадлежит плоскости a. Следовательно, этот луч пересечет плоскость p1 в линии пересечения плоскостей a и p1, т. е. в точке К1, принадлежащей проекции прямой а1. 4. Если точка К делит отрезок АD в отношении m: n то и проекция этой точки делит в таком же отношении проекцию этого отрезка (рис. 1.6):
Фигура ADD1A1 – трапеция. Прямая КК1 параллельна основаниям трапеции АА1 и DD1, следовательно делит ее стороны АD и А1D1 на пропорциональные части. 5. Проекция точки пересечения прямых есть точка пересечения проек ций этих прямых (рис. 1.7)
Рис. 1.7. Пример инвариантного свойства 5
Действительно, точка К принадлежит одновременно прямым АВ и CD. По третьему инвариантному свойству проекция этой точки К1 должна принадлежать проекциям этих прямых, т. е. должна являться точкой пересечения этих проекций. 6. Проекции параллельных прямых параллельны (рис. 1.8)
Рис. 1.8. Пример инвариантного свойства 6
Лучевые плоскости a и b, проходят через параллельные прямые АВ и CD. Они параллельны, т.к. две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости (АВ½÷ CD и АА1÷÷ СС1). Но две параллельные плоскости пересекаются с третьей по параллельным прямым, следовательно, А1В1÷÷ С1D1. 7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
Рис. 1.9. Примеры инвариантных свойств 7, 8
8. Прямая, параллельная направлению проецирования, проецируется в точку (рис. 1.9) 9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре (рис. 1.10). Следствия этого инвариантного свойства следующие: 1. Проекция отрезка прямой, параллельной плоскости проекций, конгруэнтна и параллельна самому отрезку (рис. 1.10): 2. Проекция угла, стороны которого параллельны плоскости проекций, конгруэнтна этому углу (рис. 1.10)
Рис. 1.10. Пример инвариантного свойства 9 (следствия инвариантных свойств) Ортогональное проецирование
Ортогональное проецирование является частным случаем параллельного проецирования, когда направление проецирования S перпендикулярно (ортогонально) плоскости проекций S ^ p1 (рис. 1.11).
Рис. 1.11. Ортогональная проекция прямого угла Ортогональное проецирование находит широкое применение в инженерной практике для изображения геометрических фигур на плоскости, т. к. обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием к которым можно отнести: а) простоту графических построений для определения ортогональных проекций точек; б) возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. Указанные преимущества обеспечили широкое применение ортогонального проецирования в технике, в частности для составления машиностроительных чертежей. Для ортогонального проецирования справедливы все девять инвариантных свойств, рассмотренных выше. Кроме того, необходимо отметить еще одно, десятое, инвариантное свойство, которое справедливо только для ортогонального проецирования. 10. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 1.11) На рис. 1.11 показан прямой угол АВD, обе стороны которого параллельны плоскости проекций p1. По инвариантному свойству 9.2 этот угол проецируется на плоскость p1 без искажения, т. е. ÐА1В1D1=90°. Возьмем на проецирующем луче DD1 произвольную точку С, тогда полученный ÐАВС будет прямым, т. к. АВ^ВВ1DD1. Проекцией этого прямого угла АВС, у которого только одна сторона АВ параллельна плоскости проекций p1, будет прямой угол А1В1D1. Говоря о геометрических фигурах и их проекциях необходимо помнить, что проекцией фигуры называют множество проекций всех ее точек.
1.6. Система трех плоскостей проекций. Эпюр Монжа.
Все пространственные геометрические фигуры могут быть ориентированы относительно декартовой прямоугольной системы координатных осей - системы трех взаимно перпендикулярных координатных плоскостей (рис. 1.12).
Рис. 1.12. Изображение системы трех плоскостей проекций Эти координатные плоскости обозначаются: 1. горизонтальная плоскость проекций - p1; 2. фронтальная плоскость проекций - p2; 3. профильная плоскость проекций - p3. Линии пересечения этих плоскостей образуют координатные оси: ось абсцисс – Х; ось ординат – Y; ось аппликат – Z. Точка О пересечения координатных осей принимается за начало координат и обозначается буквой О. Положительными направлениями осей считают: для оси x − влево от начала координат, для оси Y − в сторону зрителя от плоскости p2, для оси z – вверх от плоскости p1; противоположные направления считают отрицательными. Для упрощения дальнейших рассуждений будем рассматривать только часть пространства, расположенную влево от профильной плоскости проекций p3. При таком допущении три координатные плоскости проекций образуют четыре пространственных угла – октанта (в общем случае – 8 октантов). Из рис. 1.12 видно, что ось абсцисс Х делит горизонтальную плоскость проекций p1 на две части: переднюю полу p1 (оси Х и Y) и заднюю полу p1 (оси Х и - Y). Ось абсцисс Х делит фронтальную плоскость проекций p2 также на две части: верхнюю полу p2 (оси Х и Z) и нижнюю полу p2 (оси Х и - Z). Оси ординат Y и аппликат Z делят профильную плоскость проекций p3 на четыре части: 1. верхнюю переднюю полу p3 (оси Y и Z) 2. верхнюю заднюю полу p3 (оси –Y и Z) 3. нижнюю переднюю полу p3 (оси Y и –Z) 4. нижнюю заднюю полу p3 я(оси – Y и –Z)
Для того, чтобы получить плоскую (двухмерную) модель пространственных координатных плоскостей проекций, горизонтальную p1 и профильную p3 плоскости совмещают с фронтальной p2 в том порядке как это показано стрелками на рис. 1.12.
Полученное таким обра- зом совмещение трех плоскос- тей проекций (рис. 1.13) явля- ется плоской моделью систе- мы трех пространственных
Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций p1, p2 и p3, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром Монжа. Порядок построения эпюры точки, расположенной в первом октанте. На рис. 1.13 изображена пространственная точка А, координаты которой (x, y, z) показывают величины расстояний, на которые точка удалена от плоскостей проекций.
Точки пересечения этих перпендикуляров с плоскостями проекций образуют проекции точки А: А1 – горизонтальную проекцию точки; А2 – фронтальную проекцию точки;
На рис. 1.14 плоскости проекций p1 и p3 совмещены с плоскостью чертежа (с плоскостью проекции p2), а вместе с ними совмещены с плоскостью чертежа и проекции точки А (А1, А2, А3) и таким образом получена плоскостная модель координатных плоскостей проекций и плоскостная модель пространственной точки А – ее эпюра. Положение проекций точки А на эпюре однозначно определяется ее тремя координатами (рис. 1.14). На рис. 1.13 и рис. 1.14 также видно, что на эпюре горизонтальная и фронтальная проекции точки лежат на одном перпендикуляре к оси Х, а также фронтальная и профильная проекции – на одном перпендикуляре к оси Z:
А1А2 ^ Х, А2А3 ^ Z.
Из рис 1.12 видно, что точки, расположенные в различных октантах, имеют определенные знаки координат. В таблице приведены знаки координат точек, расположенных в различных октантах
Таблица знаков координат
Лекция 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S – центра проецирования (рис. 1.2).
Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S – центра проецирования (рис. 1.2).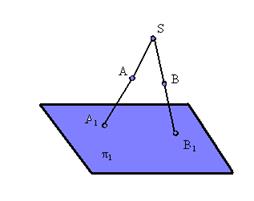








 Исключение составляет многоугольник (плоская ломаная или кривая линия) расположенный в проецирующей (лучевой) плоскости. Такой многоугольник проецируется в прямую линию (рис. 9).
Исключение составляет многоугольник (плоская ломаная или кривая линия) расположенный в проецирующей (лучевой) плоскости. Такой многоугольник проецируется в прямую линию (рис. 9).



 При этом горизонтальная плоскость проекций p1 вращается вокруг оси Х на 90°, а профильная плос- кость проекций p3 вращается вокруг оси Z также на 90° (на- правление вращения показано на рис. 1.12).
При этом горизонтальная плоскость проекций p1 вращается вокруг оси Х на 90°, а профильная плос- кость проекций p3 вращается вокруг оси Z также на 90° (на- правление вращения показано на рис. 1.12). Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций.
Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций. А3 – профильную проекцию точки.
А3 – профильную проекцию точки.


