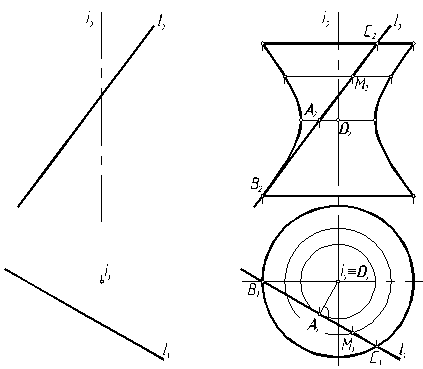Свойства параллельного проецирования

Центральное проецирование

Суть метода заключается в том, что предметы (точки, прямые, плоскости, поверхности), находящиеся в пространстве, проецируются на некоторую плоскость лучами, выходящими из одной точки.

Изображение предметов при помощи центрального проецирования обладает хорошей наглядностью, но по такому изображению трудно определить истинную форму и размеры предмета. Проецирование широко применяется в изобразительном искусстве (при построении перспективы), в кинематографии.

При составлении машиностроительных чертежей пользуются другим методом проецирования – параллельным.

Параллельное проецирование

Существо метода заключается в том, что проецирующие лучи выходят из точки, которая удалена от плоскости проекции в бесконечность. В этом случае проецирующие лучи можно считать параллельными между собой.

Параллельное проецирование отрезка АВ на плоскость П' представлено на рис. 1.1. Лучи, выходящие из точек А и В, параллельны между собой и параллельны заданному лучу .

 

Свойства параллельного проецирования

Параллельное проецирование обладает большими возможностями решения графических задач на основе таких свойств: проекцией точки является точка, прямой – прямая линия, параллельных прямых – параллельные прямые. Если точка делит отрезок прямой в некотором отношении, то и проекции отрезка находятся в таком же отношении.

В зависимости от направления проецирующего луча по отношению к плоскости П' параллельное проецирование может быть косоугольным (φ ≠ 90°) или прямоугольным (φ = 90°) – ортогональным.

Все машиностроительные чертежи выполняются на основе ортогонального проецирования, так как в этом случае легко устанавливается соотношение между длиной отрезка и его проекциями и соблюдается свойство о проецировании прямого угла плоскости. Читается это свойство так: прямой угол проецируется на плоскость в общем случае с искажением, но одна из сторон пря-
мого угла параллельна плоскости проекций – в этом случае проекция прямого угла – 90°. Это свойство является важным при решении геометрических задач.

Рассмотренные методы проецирования предмета на одну плоскость проекций позволяют однозначно решать прямую задачу, т. е. по данному оригиналу строить его чертежи. Однако обратная задача – по данному чертежу воспроизвести оригинал – не решается однозначно. В этом случае говорят – “чертеж необратим”. Для получения обратимых чертежей существуют различные методы дополнения однокартинного чертежа.

 

Прямые общего положения

Прямые общего положения наклонены ко всем плоскостям проекций и пересекают их. Точки пересечения прямой с плоскостями проекций называются следами прямой. Иногда бывает необходимо их определять. Пусть на чертеже дана прямая а, определим ее следы (рис. 3.1).

Чтобы определить точку пересечения прямой с горизонтальной плоскостью проекций – горизонтальный след, надо продолжить фронтальную проекцию прямой а_α до пересечения с осью X, провести перпендикуляр к оси X, продолжить горизонтальную проекцию прямой а₁ до пересечения с перпендикуляром. Горизонтальный след обозначается буквой Н. Необходимо обратить внимание на то, что сама точка Н присутствует на чертеже, так как Z = 0, т. е. точка принадлежит плоскости П₁.

Чтобы определить фронтальный след F, надо продолжить горизонтальную проекцию прямой до пересечения с осью X, провести перпендикуляр к оси X, продолжить фронтальную проекцию прямой до пересечения с перпендикуляром. Точка F также присутствует на чертеже и совпадает со своей фронтальной проекцией, так как координата Y = 0.

Прямые частного положения

Прямые частного положения расположены параллельно плоскостям проекций или перпендикулярно им.

Прямые, параллельные плоскостям проекций П₁, П₂, П₃, называются горизонталью (h), фронталью (f) и профильной прямой (p) (рис. 3.2).

а б в

 

Рис. 3.2

 

Прямые, перпендикулярные плоскости проекций П₁, П₂, П₃, называются горизонтально (а), фронтально (б) и профильно (в) проецирующими (рис. 3.3).

а б в

 

Рис. 3.3

Плоскости общего положения

Плоскости общего положения наклонены ко всем плоскостям проекций и пересекают их. Линии пересечения плоскости с плоскостями проекции называются следами. Часто плоскость задают следами. Чтобы перейти к заданию плоскости следами, необходимо определить следы двух прямых, лежащих в этой плоскости. Пусть дана плоскость треугольником АВС. Определим следы этой плоскости (рис. 3.4).

 

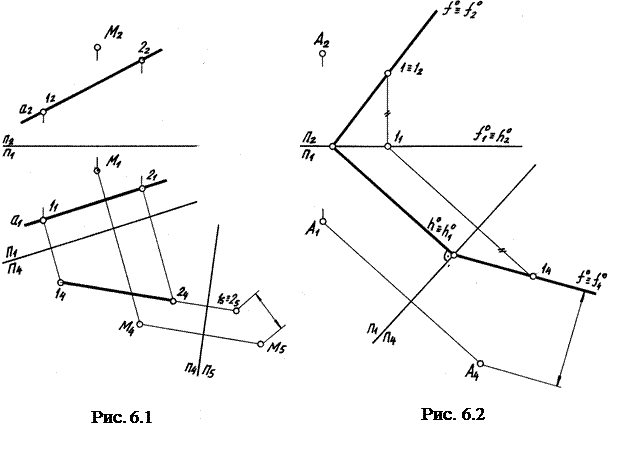
Сначала определим фронтальный след плоскости. Для этого построим фронтальные следы двух сторон треугольника – АВ и ВС. Через полученные точки F и F' проводим фронтальный след плоскости f ⁰ до пересечения с осью X и получаем точку схода следов S, из которой пойдет и горизонтальный след плоскости. Для этого построения достаточно определить горизонтальный след одной какой-либо прямой (например, АС). Тогда через S и H проводим h⁰ – горизонтальный след плоскости. След плоскости можно строить, проводя его через один след какой-то прямой параллельно направлению линии уровня (горизонтали или фронтали), так как горизонталь и фронталь – это линии, параллельные горизонтальному и фронтальному следам плоскости соответственно.

Определение расстояний

1) Между двумя точками. Решение сводится к определению натуральной величины отрезка способом прямоугольного треугольника.

2) Между прямой и точкой. Решение – прямую преобразовать в проецирующую прямую (рис. 6.1).

3) Между точкой и плоскостью. Решение – плоскость преобразовать в проецирующую (рис. 6.2).

4) Между двумя параллельными прямыми. Решение – на одной прямой взять точку, вторую преобразовать в проецирующую.

5) Между двумя скрещивающимися прямыми. Решение – одну из прямых преобразовать в проецирующую прямую (рис. 6.3).

6) Между прямой и параллельной ей плоскостью. Решение – на прямой взять точку и плоскость преобразовать в проецирующую.

7) Между двумя параллельными плоскостями. Решение – на одной из плоскостей проекций взять точку, а вторую плоскость преобразовать в проецирующую.

Рис. 6.3

 

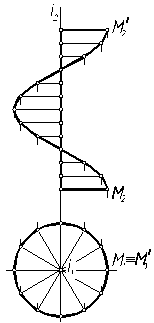
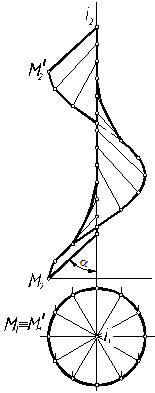
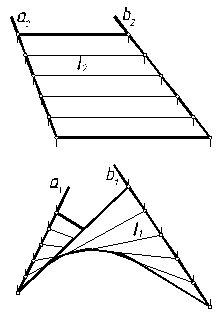
Образование поверхностей. Классификация

В начертательной геометрии образование поверхностей рассматривают как результат движения некоторой образующей линии по направляющей. И образующая, и направляющая могут быть прямыми или кривыми линиями. В зависимости от вида образующей и закона изменения направляющей получается та или иная поверхность.

Если образующей является прямая линия, то поверхность называется линейчатой. К линейчатым поверхностям относятся следующие:

конические – образованы перемещением образующей по некоторой направляющей, причем образующая имеет одну неподвижную точку, которая называется вершиной конической поверхности;

цилиндрические – образующая, перемещаясь по направляющей, всегда остается параллельной некоторой заданной прямой;

винтовые – прямолинейная образующая перемещается по винтовой линии, причем угол между образующей и осью вращения остается постоянным;

поверхности с плоскостью параллелизма – прямая перемещается по двум скрещивающимся линиям, оставаясь всегда параллельной некоторой плоскости, называемой плоскостью параллелизма. Среди поверхностей с плоскостью
параллелизма различают цилиндроиды – направляющими являются две скре-щивающиеся кривые; коноиды – направляющие – скрещивающиеся линии, но одна из них прямая; косая плоскость – направляющие – две скрещивающиеся прямые.

В качестве примера линейчатой поверхности на рис. 7.1, 7.2 приведены конус, цилиндр, прямой и наклонный геликоиды, косая плоскость. Если поверхности образованы вращением образующей вокруг некоторой прямой, то их называют поверхностями вращения.

 

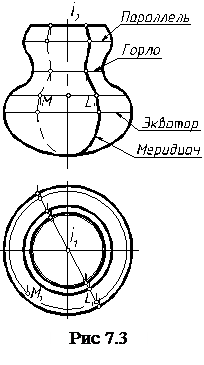
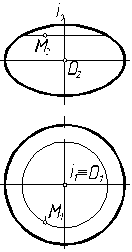
а б в

Рис. 7.1

Образующая поверхности вращения, лежащая в плоскости, проходящей через ось вращения, называется меридианом. Сечение поверхности плоскостью, перпендикулярной оси, является окружностью, его называют параллелью. Параллель с наименьшим радиусом называют горлом, с наибольшим – экватором (рис. 7.3).

а б

Рис. 7.2

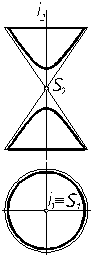
Задание и изображение поверхностей

На чертеже

Из всех возможных способов образования поверхности необходимо выбирать такие, которые являются наиболее простыми и более удобными для изображения или для решения данной задачи. Чтобы задать поверхность на комплексном чертеже, достаточно иметь на нем такие элементы поверхности, которые позволяют построить каждую ее точку. Совокупность этих элементов поверхности называют определителем поверхности.

Часто поверхность задается проекциями своих направляющих и указывается способ построения ее образующих. Для придания чертежу большей наглядности в большинстве случаев на нем строят еще и очерк поверхности. Очерком поверхности называют проекции контурной линии.

Приведем примеры изображения некоторых поверхностей.

1. Пусть поверхность (однополостный гиперболоид) задана на чертеже (рис. 7.4) определителем: образующая l вращается вокруг скрещивающейся с ней осью i. Требуется построить очерк этой поверхности.

Решение выполним на рис. 7.5. При вращении прямой l вокруг оси i все точки прямой опишут окружности различных радиусов. Возьмем на прямой четыре точки и построим проекции окружностей при их вращении. Точка А вращается по окружности наименьшего радиуса АО, т. е. эта окружность является горлом поверхности. Точки В и С в рассматриваемом примере вращаются по окружности одинакового радиуса. Произвольная точка М выбрана между горлом и верхним основанием этой поверхности. На горизонтальной проекции очерком поверхности будет являться окружность. На фронтальной, соединив крайние точки проекции окружностей точек, получим очерк, представляющий собой ветви гиперболы. Таким образом, построены проекции однополостного гиперболоида.

 

Рис. 7.4 Рис. 7.5

 

По классификации эта поверхность может быть отнесена и к линейчатым (образующая – прямая), и к нелинейчатым (образующая – гипербола).

2. Построить проекции цилиндра вращения. Решение – поверхность образована вращением прямой вокруг параллельной ей оси (рис. 7.6).

3. Построить проекции конуса вращения. Решение – поверхность образована вращением прямой вокруг пересекающейся с ней оси (рис. 7.7).

Рис. 7.6 Рис. 7.7 Рис. 7.8

 

4. Построить проекции тора. Решение – поверхность образована вращением окружности вокруг оси i, не проходящей через ее центр (рис. 7.8).

5. Построить проекции эллипсоида. Решение – поверхность образована вращением эллипса вокруг оси (рис. 7.9).

6. Построить проекции параболоида. Решение – поверхность образована вращением параболы вокруг оси i (рис. 7.10).

Рис. 7.9 Рис. 7.10 Рис. 7.11

7. Построить проекции двуполостного гиперболоида вращения. Реше-
ние – поверхность образована вращением гиперболы вокруг ее действительной
оси i (рис. 7.11).

Более подробные сведения о классификации и изображении поверхностей можно получить в работах [1 – 4].

 

Центральное проецирование

Суть метода заключается в том, что предметы (точки, прямые, плоскости, поверхности), находящиеся в пространстве, проецируются на некоторую плоскость лучами, выходящими из одной точки.

Изображение предметов при помощи центрального проецирования обладает хорошей наглядностью, но по такому изображению трудно определить истинную форму и размеры предмета. Проецирование широко применяется в изобразительном искусстве (при построении перспективы), в кинематографии.

При составлении машиностроительных чертежей пользуются другим методом проецирования – параллельным.

Параллельное проецирование

Существо метода заключается в том, что проецирующие лучи выходят из точки, которая удалена от плоскости проекции в бесконечность. В этом случае проецирующие лучи можно считать параллельными между собой.

Параллельное проецирование отрезка АВ на плоскость П' представлено на рис. 1.1. Лучи, выходящие из точек А и В, параллельны между собой и параллельны заданному лучу .

 

Свойства параллельного проецирования

Параллельное проецирование обладает большими возможностями решения графических задач на основе таких свойств: проекцией точки является точка, прямой – прямая линия, параллельных прямых – параллельные прямые. Если точка делит отрезок прямой в некотором отношении, то и проекции отрезка находятся в таком же отношении.

В зависимости от направления проецирующего луча по отношению к плоскости П' параллельное проецирование может быть косоугольным (φ ≠ 90°) или прямоугольным (φ = 90°) – ортогональным.

Все машиностроительные чертежи выполняются на основе ортогонального проецирования, так как в этом случае легко устанавливается соотношение между длиной отрезка и его проекциями и соблюдается свойство о проецировании прямого угла плоскости. Читается это свойство так: прямой угол проецируется на плоскость в общем случае с искажением, но одна из сторон пря-
мого угла параллельна плоскости проекций – в этом случае проекция прямого угла – 90°. Это свойство является важным при решении геометрических задач.

Рассмотренные методы проецирования предмета на одну плоскость проекций позволяют однозначно решать прямую задачу, т. е. по данному оригиналу строить его чертежи. Однако обратная задача – по данному чертежу воспроизвести оригинал – не решается однозначно. В этом случае говорят – “чертеж необратим”. Для получения обратимых чертежей существуют различные методы дополнения однокартинного чертежа.