
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы дополнения однокартинного чертежаСодержание книги
Поиск на нашем сайте
Способ с числовыми отметками. Суть способазаключается в том, что недостающая в плоскости проекций пространственная координата отмечается на чертеже числом. Этот способ широко применяется в топографии, при пост-роении профиля дорог, в том числе железнодорожного пути. Способ академика Федорова. Принципиальное отличие от предыдущего способа состоит в том, что числовые отметки заменяются масштабными отрезками. Способ в основном применяется в кристаллографии. Способ составления аксонометрических проекции применяют в строительных и машиностроительных чертежах в основном для наглядного изображения предмета. Способ составления комплексного чертежа наиболее широко применяется при составлении строительных и машиностроительных чер-
2. ТОЧКА, ПРЯМАЯ И ПЛОСКОСТЬ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Прежде чем перейти к изображению геометрических элементов на комп-лексном чертеже, рассмотрим положение некоторой точки А в пространственной системе координат – X, Y, Z (рис. 2.1).
На таком комплексном чертеже точка будет изображаться своими проекциями. Чтобы точка на чертеже была задана, достаточно иметь две ее проекции. Размеры представляются на комплексном чертеже в натуральную величину. Предмет можно изучать спереди, сверху, слева, но при этом необходимо иметь навыки пространственного представления на таком чертеже. Прямая на комплексном чертеже может быть задана двумя точками или своими проекциями. Минимальное количество проекций прямой на чертеже – две (рис. 2.3).
а б Рис. 2.3
3. ПРЯМЫЕ И ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Прямые общего положения Прямые общего положения наклонены ко всем плоскостям проекций и пересекают их. Точки пересечения прямой с плоскостями проекций называются следами прямой. Иногда бывает необходимо их определять. Пусть на чертеже дана прямая а, определим ее следы (рис. 3.1). Чтобы определить точку пересечения прямой с горизонтальной плоскостью проекций – горизонтальный след, надо продолжить фронтальную проекцию прямой аα до пересечения с осью X, провести перпендикуляр к оси X, продолжить горизонтальную проекцию прямой а1 до пересечения с перпендикуляром. Горизонтальный след обозначается буквой Н. Необходимо обратить внимание на то, что сама точка Н присутствует на чертеже, так как Z = 0, т. е. точка принадлежит плоскости П1.
Прямые частного положения Прямые частного положения расположены параллельно плоскостям проекций или перпендикулярно им. Прямые, параллельные плоскостям проекций П1, П2, П3, называются горизонталью (h), фронталью (f) и профильной прямой (p) (рис. 3.2).
а б в
Рис. 3.2
Прямые, перпендикулярные плоскости проекций П1, П2, П3, называются горизонтально (а), фронтально (б) и профильно (в) проецирующими (рис. 3.3).
а б в
Рис. 3.3 Плоскости общего положения Плоскости общего положения наклонены ко всем плоскостям проекций и пересекают их. Линии пересечения плоскости с плоскостями проекции называются следами. Часто плоскость задают следами. Чтобы перейти к заданию плоскости следами, необходимо определить следы двух прямых, лежащих в этой плоскости. Пусть дана плоскость треугольником АВС. Определим следы этой плоскости (рис. 3.4).
Сначала определим фронтальный след плоскости. Для этого построим фронтальные следы двух сторон треугольника – АВ и ВС. Через полученные точки F и F' проводим фронтальный след плоскости f 0 до пересечения с осью X и получаем точку схода следов S, из которой пойдет и горизонтальный след плоскости. Для этого построения достаточно определить горизонтальный след одной какой-либо прямой (например, АС). Тогда через S и H проводим h0 – горизонтальный след плоскости. След плоскости можно строить, проводя его через один след какой-то прямой параллельно направлению линии уровня (горизонтали или фронтали), так как горизонталь и фронталь – это линии, параллельные горизонтальному и фронтальному следам плоскости соответственно.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.143.1 (0.009 с.) |


 Спроецируем ортогонально точку А на три взаимоперпендикулярные плоскости проекций П1,П2,П3 и получим проекции этой точки: А1 – горизонтальная; А2 – фронтальная,
Спроецируем ортогонально точку А на три взаимоперпендикулярные плоскости проекций П1,П2,П3 и получим проекции этой точки: А1 – горизонтальная; А2 – фронтальная, 
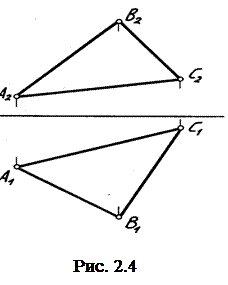 Плоскость на комплексном чертеже может быть задана тремя точками, точкой и прямой, двумя пересекающимися прямыми, двумя параллельными прямыми, плоской геометрической фигурой (треугольник, окружность и т. д.) и др. Плоскость на комплексном чертеже определяют две ее проекции (рис. 2.4).
Плоскость на комплексном чертеже может быть задана тремя точками, точкой и прямой, двумя пересекающимися прямыми, двумя параллельными прямыми, плоской геометрической фигурой (треугольник, окружность и т. д.) и др. Плоскость на комплексном чертеже определяют две ее проекции (рис. 2.4). Чтобы определить фронтальный след F, надо продолжить горизонтальную проекцию прямой до пересечения с осью X, провести перпендикуляр к оси X, продолжить фронтальную проекцию прямой до пересечения с перпендикуляром. Точка F также присутствует на чертеже и совпадает со своей фронтальной проекцией, так как координата Y = 0.
Чтобы определить фронтальный след F, надо продолжить горизонтальную проекцию прямой до пересечения с осью X, провести перпендикуляр к оси X, продолжить фронтальную проекцию прямой до пересечения с перпендикуляром. Точка F также присутствует на чертеже и совпадает со своей фронтальной проекцией, так как координата Y = 0.





