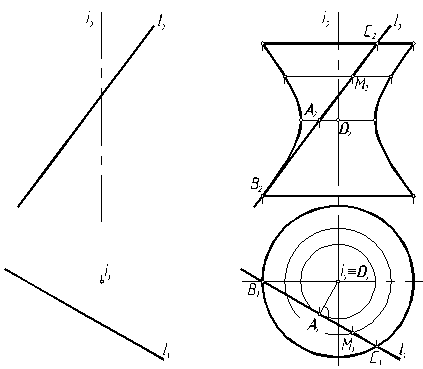Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение углов наклона прямыхСодержание книги
Поиск на нашем сайте
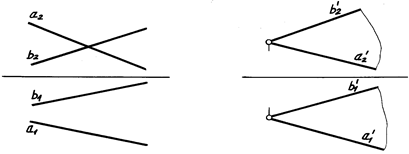
1) Между двумя пересекающимися прямыми. Решение – преобразовать плоскость, заданную двумя пересекающимися прямыми, в плоскость уровня. 2) Между двумя скрещивающимися прямыми. Решение – скрещивающиеся прямые заменяют пересекающимися таким образом, чтобы их положение в пространстве по отношению к плоскостям проекций не изменилось. Затем плоскость, заданную двумя пересекающимися прямыми, преобразовать в плоскость уровня (рис. 6.4).
а б Рис. 6.4 3) Между прямой и плоскостью. Решение – из точки, взятой на прямой, опускают перпендикуляр n на плоскость, тогда прямая и перпендикуляр составляют плоскость. Эту плоскость преобразуют в плоскость уровня и определяют угол Искомый угол
Рис. 6.5 4) Между двумя гранями. Решение – линию пересечения двух плоскостей (общее ребро двугранного угла) преобразуют в проецирующее положение
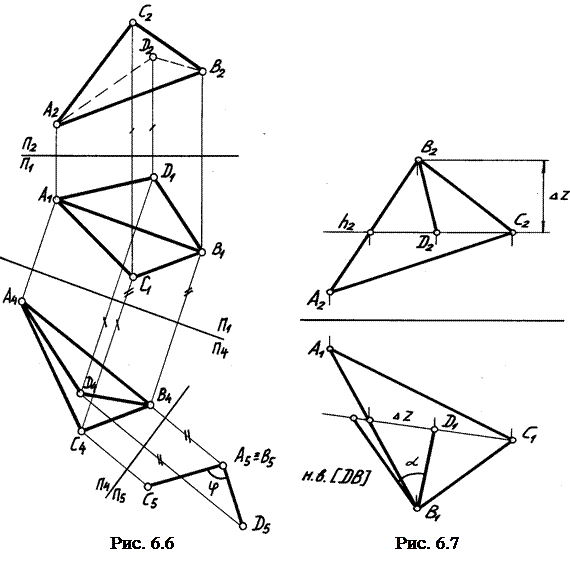
Определение угла наклона плоскости к плоскости проекции Р е ш е н и е 1. Проводят линии наибольшего наклона плоскости и способом прямоугольного треугольника определяют угол наклона этих прямых к Линии наибольшего наклона – эта линии, лежащие в заданной плоскости и перпендикулярные линиям уровня (или следам плоскости). П р и м е р. Дана плоскость треугольника АВС. Определить угол наклона треугольника АВС к П1 (рис. 6.7). В плоскости проводим горизонталь h и из точки В опускаем перпендикуляр к горизонтали, т. е. линию наибольшего наклона к П1. Способом прямоугольного треугольника определяем натуральную величину отрезка ВD. Угол между натуральной величиной и горизонтальной проекцией отрезка и является углом наклона АВС к П1. Р е ш е н и е 2. Заданную плоскость преобразуют в плоскость проецирующую, т. е. решают третью задачу на преобразование (см. рис. 5.4).
7. ПОВЕРХНОСТИ
Образование поверхностей. Классификация В начертательной геометрии образование поверхностей рассматривают как результат движения некоторой образующей линии по направляющей. И образующая, и направляющая могут быть прямыми или кривыми линиями. В зависимости от вида образующей и закона изменения направляющей получается та или иная поверхность.
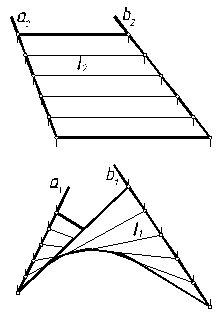
Если образующей является прямая линия, то поверхность называется линейчатой. К линейчатым поверхностям относятся следующие: конические – образованы перемещением образующей по некоторой направляющей, причем образующая имеет одну неподвижную точку, которая называется вершиной конической поверхности; цилиндрические – образующая, перемещаясь по направляющей, всегда остается параллельной некоторой заданной прямой; винтовые – прямолинейная образующая перемещается по винтовой линии, причем угол между образующей и осью вращения остается постоянным; поверхности с плоскостью параллелизма – прямая перемещается по двум скрещивающимся линиям, оставаясь всегда параллельной некоторой плоскости, называемой плоскостью параллелизма. Среди поверхностей с плоскостью В качестве примера линейчатой поверхности на рис. 7.1, 7.2 приведены конус, цилиндр, прямой и наклонный геликоиды, косая плоскость. Если поверхности образованы вращением образующей вокруг некоторой прямой, то их называют поверхностями вращения.
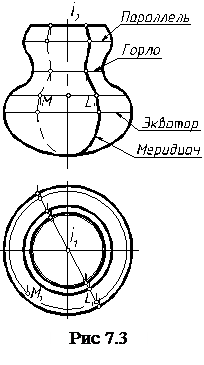
а б в Рис. 7.1 Образующая поверхности вращения, лежащая в плоскости, проходящей через ось вращения, называется меридианом. Сечение поверхности плоскостью, перпендикулярной оси, является окружностью, его называют параллелью. Параллель с наименьшим радиусом называют горлом, с наибольшим – экватором (рис. 7.3).
а б Рис. 7.2
Задание и изображение поверхностей На чертеже Из всех возможных способов образования поверхности необходимо выбирать такие, которые являются наиболее простыми и более удобными для изображения или для решения данной задачи. Чтобы задать поверхность на комплексном чертеже, достаточно иметь на нем такие элементы поверхности, которые позволяют построить каждую ее точку. Совокупность этих элементов поверхности называют определителем поверхности. Часто поверхность задается проекциями своих направляющих и указывается способ построения ее образующих. Для придания чертежу большей наглядности в большинстве случаев на нем строят еще и очерк поверхности. Очерком поверхности называют проекции контурной линии.
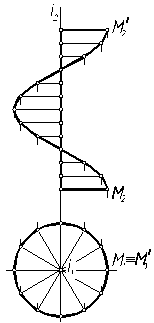
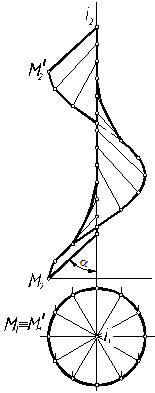
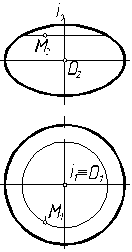
Приведем примеры изображения некоторых поверхностей. 1. Пусть поверхность (однополостный гиперболоид) задана на чертеже (рис. 7.4) определителем: образующая l вращается вокруг скрещивающейся с ней осью i. Требуется построить очерк этой поверхности. Решение выполним на рис. 7.5. При вращении прямой l вокруг оси i все точки прямой опишут окружности различных радиусов. Возьмем на прямой четыре точки и построим проекции окружностей при их вращении. Точка А вращается по окружности наименьшего радиуса АО, т. е. эта окружность является горлом поверхности. Точки В и С в рассматриваемом примере вращаются по окружности одинакового радиуса. Произвольная точка М выбрана между горлом и верхним основанием этой поверхности. На горизонтальной проекции очерком поверхности будет являться окружность. На фронтальной, соединив крайние точки проекции окружностей точек, получим очерк, представляющий собой ветви гиперболы. Таким образом, построены проекции однополостного гиперболоида.
Рис. 7.4 Рис. 7.5
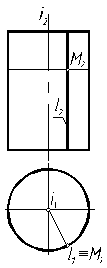
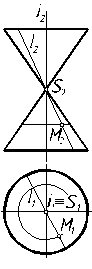
По классификации эта поверхность может быть отнесена и к линейчатым (образующая – прямая), и к нелинейчатым (образующая – гипербола). 2. Построить проекции цилиндра вращения. Решение – поверхность образована вращением прямой вокруг параллельной ей оси (рис. 7.6). 3. Построить проекции конуса вращения. Решение – поверхность образована вращением прямой вокруг пересекающейся с ней оси (рис. 7.7).
Рис. 7.6 Рис. 7.7 Рис. 7.8
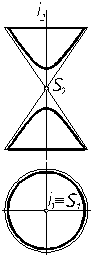
4. Построить проекции тора. Решение – поверхность образована вращением окружности вокруг оси i, не проходящей через ее центр (рис. 7.8). 5. Построить проекции эллипсоида. Решение – поверхность образована вращением эллипса вокруг оси (рис. 7.9). 6. Построить проекции параболоида. Решение – поверхность образована вращением параболы вокруг оси i (рис. 7.10).
Рис. 7.9 Рис. 7.10 Рис. 7.11 7. Построить проекции двуполостного гиперболоида вращения. Реше- Более подробные сведения о классификации и изображении поверхностей можно получить в работах [1 – 4].
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.219.213 (0.01 с.) |

 при вершине А.
при вершине А.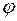 между прямой и плоскостью определяется как дополнительный в прямоугольном треугольнике:
между прямой и плоскостью определяется как дополнительный в прямоугольном треугольнике: