Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способ замены плоскостей проекцийСодержание книги
Поиск на нашем сайте
Рассмотрим применение этого способа к решению четырех основных задач на преобразование. П е р в а я з а д а ч а: прямая общего
Так как высота прямой в пространстве не изменилась, то от оси П1/П4 на соответствующих линиях связи откладываем высоту точек А и В, получаем А4 и В4. Проекции прямой А1В1 и А4В4 дают положение прямой АВ, параллельное новой фронтальной плос- Угол между натуральной величиной и фронтальной проекцией и есть угол (β) наклона прямой АВ к П2. Часто для определения натуральной величины отрезка и углов наклона прямой к плоскостям проекций пользуются способом прямоугольного треугольника, который является следствием из решения первой задачи на преобразование (рис. 5.2). Натуральная величина отрезка есть гипотенуза прямоугольного треугольника, один катет которого – сама проекция отрезка, другой катет по величине является разностью координат концов отрезка, взятой на другой плоскости проекций. В т о р а я з а д а ч а: прямая уровня преобразуется в прямую проецирующую (рис. 5.3).
Т р е т ь я и ч е т в е р т а я з а д а ч и: плоскость общего положения преобразуется в плоскость проецирующую, и плоскость проецирующая – в плоскость уровня. Решение этих двух задач приведено на рис. 5.4. Пусть дана плоскость общего положения – задана треугольником АВС. Чтобы преобразовать ее в проецирующую, нужно ввести новую плоскость проекций перпендикулярно треугольнику АВС, но на комплексном чертеже это возможно в том случае, если провести плоскость проекций перпендикулярно линиям уровня или следам плоскости.
С этой целью проведем в плоскости треугольника АВС горизонталь. Перпендикулярно h1 проведем координатную ось (П1/П2). Прямая уровня h преобразовалась в прямую проецирующую h(h1h4). Из проекции вершин треугольника А1,В1,С1 проведем линии связи и от (П1/П4) отложим соответствующие координаты А2,В2,С2. Проекция треугольника А4,В4,С4 представляет собой прямую линию.
Рис. 5.4
Таким образом, плоскость общего положения преобразована в плоскость проецирующую. Угол между проекцией треугольника А4В4С4 и координатной осью Для преобразования проецирующей плоскости в плоскость уровня (решение четвертой задачи на преобразование), необходимо построить новую плоскость проекций параллельно проекции треугольника А4В4С4, провести линии связи и отложить координаты точек, взятые из П1, т. е. от оси П1/П4 6. РЕШЕНИЕ НЕКОТОРЫХ МЕТРИЧЕСКИХ ЗАДАЧ ПРЕОБРАЗОВАНИЯМИ КОМПЛЕКСНОГО ЧЕРТЕЖА
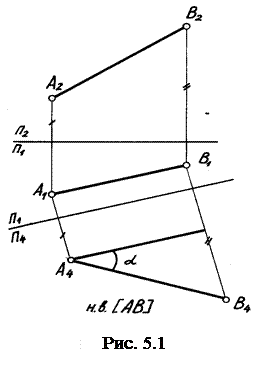
Определение расстояний 1) Между двумя точками. Решение сводится к определению натуральной величины отрезка способом прямоугольного треугольника. 2) Между прямой и точкой. Решение – прямую преобразовать в проецирующую прямую (рис. 6.1). 3) Между точкой и плоскостью. Решение – плоскость преобразовать в проецирующую (рис. 6.2).
4) Между двумя параллельными прямыми. Решение – на одной прямой взять точку, вторую преобразовать в проецирующую. 5) Между двумя скрещивающимися прямыми. Решение – одну из прямых преобразовать в проецирующую прямую (рис. 6.3). 6) Между прямой и параллельной ей плоскостью. Решение – на прямой взять точку и плоскость преобразовать в проецирующую. 7) Между двумя параллельными плоскостями. Решение – на одной из плоскостей проекций взять точку, а вторую плоскость преобразовать в проецирующую.
Рис. 6.3
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.006 с.) |

 Сущность способа заключается в том, что на чертеже вводится новая плоскость проекций таким образом, что предмет по отношению к ней занимает частное положение.
Сущность способа заключается в том, что на чертеже вводится новая плоскость проекций таким образом, что предмет по отношению к ней занимает частное положение.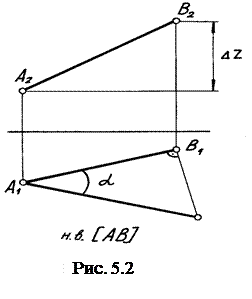 Чтобы преобразовать прямую AB общего положения в прямую уровня, необходимо ввести новую плоскость проекций параллельно АВ, т. е. на чертеже провести новую координатную ось параллельно А1В1 или А2В2. В рассматриваемом случае координатная ось П1 проведена параллельно А1В1, таким образом введена новая фронтальная плоскость проекций. Для построения проекции отрезка на этой плоскости нужно из А1 и В1 провести линии связи, перпендикулярные координатной осиП1/П4.
Чтобы преобразовать прямую AB общего положения в прямую уровня, необходимо ввести новую плоскость проекций параллельно АВ, т. е. на чертеже провести новую координатную ось параллельно А1В1 или А2В2. В рассматриваемом случае координатная ось П1 проведена параллельно А1В1, таким образом введена новая фронтальная плоскость проекций. Для построения проекции отрезка на этой плоскости нужно из А1 и В1 провести линии связи, перпендикулярные координатной осиП1/П4. Для решения этой задачи необходимо новую плоскость проекций провести перпендикулярно натуральной величине прямой А1В1. Проекции А1В1 и А4В4 дают положение прямой АВ, перпендикулярное новой фронтальной плоскости проекций П4.
Для решения этой задачи необходимо новую плоскость проекций провести перпендикулярно натуральной величине прямой А1В1. Проекции А1В1 и А4В4 дают положение прямой АВ, перпендикулярное новой фронтальной плоскости проекций П4.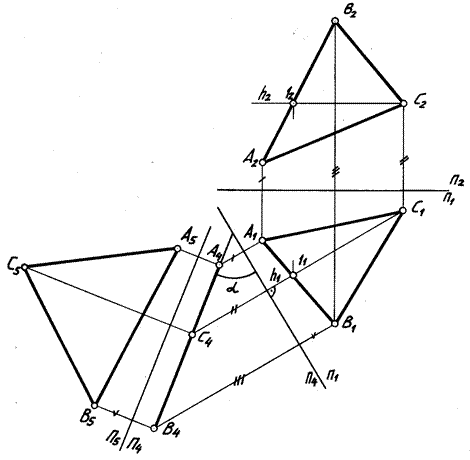
 является углом наклона плоскости к П1.
является углом наклона плоскости к П1. до А1,В1,С1. Проекция треугольника А5В5С5 является натуральной величиной треугольника АВС.
до А1,В1,С1. Проекция треугольника А5В5С5 является натуральной величиной треугольника АВС.