
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1 метод проецированияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ЛЕКЦИЯ 1 МЕТОД ПРОЕЦИРОВАНИЯ ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ Центральное проецирование является наиболее общим случаем получения проекций геометрических фигур. В основу построения любого изображения положена операция проецирования, которая заключается в следующем: в пространстве выбирают произвольную точку S – центр проецирования, и плоскость, не проходящую через точку S – плоскость проецирования
[SA) ∩ [SB) ∩
Чтобы спроецировать точку А пространства на плоскость
Проекцией фигуры называют множество проекций всех ее точек. Проекция криволинейной фигуры представляет собой линию пересечения проецирующей поверхности Свойства центрального проецирования: Так как через две различные точки можно провести одну и только одну прямую, то при заданном центре проецирования и плоскости проекций, каждая точка пространства будет иметь одну и только одну центральную проекцию.
Обратное утверждение – каждой центральной проекции точки однозначно соответствует точка пространства, не имеет смысла. Поэтому одна центральная проекция точки не дает возможности судить о положении самой точки в пространстве. Для того, чтобы сделать возможным определение положения точки в пространстве по ее центральным проекциям, необходимо иметь две центральные проекции этой точки, полученные из двух различных центров (рис.3).
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ Широкое применение в практике получил тот случай, когда центр проецирования удален в бесконечность. Проецирующие лучи при этом параллельны между собой, и проекции точек, фигур и тел получают названия параллельных проекций. В свою очередь параллельные проекции подразделяются на прямоугольные и косоугольные. В первом случае плоскость проекций с направлением проецирования образует угол 90о, а во втором не равный 90о (рис.4 и рис.5).
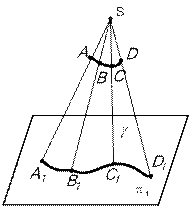
Каждой точке пространства соответствует только одна параллельная проекция. Обратное утверждение не имеет смысла. Для определения точки в пространстве необходимо иметь две ее параллельные проекции, полученные при различных направлениях проецирования (рис.6).
В дальнейшем мы будем пользоваться параллельными проекциями, ортогональными (прямоугольными) и аксонометрическими, причем первые будут прямоугольными, а вторые прямоугольными и косоугольными.
1. 3. Ортогональные проекции точки (Эпюр Монжа). Сущность метода ортогонального проецирования заключается в том, что предмет проецируется на две взаимно перпендикулярные плоскости лучами, ортогональными (перпендикулярными) к этим двум плоскостям. Одну из этих плоскостей проекций Плоскости проекций делят пространство на четыре двугранных угла (четверти) I, II, III, IV (рис.7).
При построении проекций необходимо помнить, что ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. А1 – горизонтальная проекция точки А А2 - фронтальная проекция точки А Проецирующие лучи определяют плоскость a ([АА2] АА1 = А2Ах – расстояние от точки А до АА2 = А1Ах - расстояние от точки А до Ортогональные проекции точки на две взаимно перпендикулярные плоскости вполне определяют положение точки в пространстве. Построение проекций точек в 4-х угловых пространствах показано на рис.8.
Чтобы получить плоский чертеж, плоскость Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещены определенным образом одна с другой, называется эпюром Монжа (рис.9).
Проекции одной и той же точки на две взаимно перпендикулярные плоскости располагаются на прямой, перпендикулярной оси проекций х12. Эта прямая называется направлением проецирования или линией проекционной связи.
ЛЕКЦИЯ 2 ПРЯМАЯ ЛИНИЯ Для построения изображения прямой линии на плоскостях проекций достаточно построить проекции двух точек этой прямой (рис.1).
a([ВВ2] || [АА2]) ∩
а –прямая в пространстве, a 1 – горизонтальная проекция прямой, а 2 – фронтальная проекция прямой. Проекция прямой линии есть также прямая линия. Точка, лежащая на прямой линии, имеет свои проекции на соответствующих проекциях прямой. C1 В каком отношении точка делит отрезок прямой линии в пространстве, в таком же отношении проекции этой точки делят соответствующие проекции отрезка.
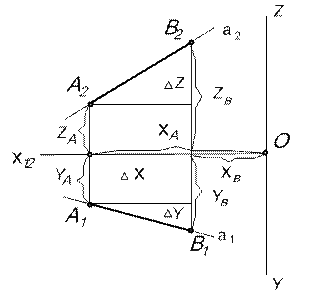
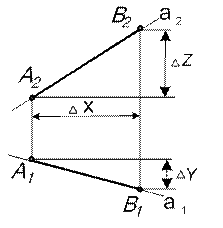
Совмещая плоскости проекций По эпюру с осями можно определить положение точек А и В в пространстве по координатам X, Y, Z. Безосный эпюр точек А и В не определяет их положение в пространстве, но позволяет судить об их относительности ориентировке (рис.2). ∆Х характеризует смещение точки А по отношению к точке В в направлении параллельном
Положение прямой относительно плоскостей проекций. 1. Прямыми общего положения называются прямые, не параллельные ни одной из плоскостей проекций (рис.1, 2, 3).
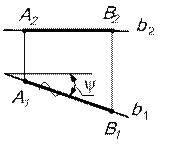
2. Прямые уровня - прямые, параллельные плоскостям проекций. а) Прямые, параллельные горизонтальной плоскости проекций, называются горизонтальными прямыми или горизонталями (рис.4)
[АВ] [А1В1] [А2В2]
b2 ┴ линии связи; b2 ║ ОХ b1 – конгруэнтна самой прямой
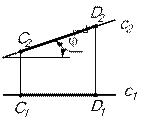
б) Прямая, параллельная
[CD] [C1D1] [C2D2]
c1┴ линии связи c1║ ОХ c2 конгруэнтна самой прямой
в) Прямая, параллельная
[MN] [M1N1] [M2N2]
3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая, перпендикулярная
Прямая, перпендикулярная
Прямая, перпендикулярная
Прямая, параллельная плоскости симметрии Прямая, параллельная плоскости тождества
ПРОЕКЦИИ ПЛОСКИХ УГЛОВ
Плоский угол проецируется на плоскость проекций в истинную величину тогда, когда обе его стороны параллельны плоскости проекций. Если стороны прямого угла произвольно расположены по отношению к плоскостям проекций, то прямой угол может проецироваться и тупым и острым. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость прямой угол спроецируется в виде прямого же угла (рис.20).
Пусть стороны АВ прямого угла АВС║
ЛЕКЦИЯ 3 ПЛОСКОСТЬ Положение плоскости в пространстве можно определить: 1. Тремя точками, не лежащими на одной прямой; 2. Прямой и точкой вне ее; 3. Двумя пересекающимися прямыми; 4. Двумя параллельными прямыми (рис.1).
Плоскость может быть задана также отсеками плоской фигуры (рис.2).
Возможны следующие положения плоскости относительно плоскостей проекций: 1.Плоскость, не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения (рис.1 и 2). 2. Частные положения плоскости: а) Плоскость, перпендикулярная к горизонтальной плоскости проекций Горизонтальные проекции всех точек и любых фигур, лежащих в горизонтально-проецирующей плоскости, совпадают со следом этой плоскости α1=
б) Плоскость, перпендикулярная к фронтальной плоскости проекций
Фронтальные проекции всех точек и фигур, лежащих в этой плоскости, совпадают с ее фронтальным следом. Угол φ между плоскостью
Плоскость, перпендикулярная к профильной плоскости проекций называется профильно-проецирующей плоскостью. Частный случай, когда профильно-проецирующая плоскость проходит через ось ОХ и делит пополам угол между плоскостями
Основные свойства проецирующих плоскостей состоят в том, что все геометрические образы, лежащие в них, на одной из плоскостей проекций изображаются прямой, совпадающей со следом плоскости, т.е. с линией пересечения проецирующей плоскости с соответствующей плоскостью проекций. Плоскости, перпендикулярные к двум плоскостям проекций, называется плоскостями уровня. Плоскость δ а) Плоскость δ, параллельная горизонтальной плоскости проекций
б) Плоскость
Любая фигура, расположенная в этой плоскости, проецируется на Все геометрические образы, расположенные в плоскостях, параллельных плоскостям проекций, проецируются на эти плоскости проекций без искажения. 3.2. ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ 1. Прямая принадлежит плоскости, если она имеет с этой плоскостью две общие точки (рис.8). 2. Прямая принадлежит плоскости, если она имеет с плоскостью одну общую точку и параллельна прямой, лежащей в этой плоскости (рис.9).
Построение точки в плоскости производится, исходя из условия, что она должна находиться на прямой, лежащей в этой плоскости. Т.о. задача на построение точки в плоскости сводится к задаче на построение прямой в этой плоскости (рис.10). Чтобы построить горизонтальную проекцию точки М, принадлежащей плоскости
3.3. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ Главными линиями плоскости называются прямые, лежащие в данной плоскости и параллельные плоскостям проекций Линии наибольшего ската – прямые, проведенные по плоскости перпендикулярно к горизонталям (рис.12). Линия наибольшего ската и ее горизонтальная проекция образуют линейный угол, которым измеряется двугранный угол, составленный плоскостью С помощью главных линий плоскости оказывается удобным решать вопросы о взаимном расположении точки и плоскости (рис.13). Дана плоскость
ЛЕКЦИЯ 4 ДВЕ ПЛОСКОСТИ. Две плоскости могут быть параллельны друг к другу или пересекаться между собой.
Параллельные плоскости. Две плоскости параллельны, если в каждой из них можно построить по две пересекающихся между собой прямые линии так, чтобы прямые одной плоскости были соответственно параллельны прямым другой плоскости.
Наиболее простой случай – параллельность двух проецирующих плоскостей. Здесь достаточно параллельности следов плоскостей (рис.1). В случае параллельности плоскостей общего положения необходимо в каждой из них указать по две соответственно параллельные прямые (рис.2). В качестве таких прямых можно взять главные линии плоскости или какие-то другие прямые.
Пересекающиеся плоскости. Основная задача – построение линии пересечения двух плоскостей, которая вполне определяется двумя точками, принадлежащими обеим плоскостям: а) проецирующие Проецирующие плоскости одного наименования, как перпендикулярные к одной и той же плоскости проекций, пересекаются по прямой линии также перпендикулярной к этой плоскости проекций (рис.3). Проецирующие плоскости разных наименований пересекаются по прямой, для которой они будут проецирующими плоскостями (рис.4).
б) Наиболее просто решается задача, если одна из пересекающихся плоскостей проецирующая (рис.5).
в) Две плоскости общего положения. Рассмотрим случай пересечения плоскостей общего положения (рис.6).
Три плоскости пересекаются в одной точке, поэтому общий метод построения точек линии пересечения состоит в следующем: две пересекающиеся плоскости пересекаются третьей, вспомогательной плоскостью.
Через точки K и L проводим линию пересечения ℓ (рис.7).
Некоторого упрощения можно достичь, если вспомогательные плоскости проводить через прямые, задающие плоскости (рис.8).
ЛЕКЦИЯ 5 МЕТОДЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА. Многие пространственные задачи в общем виде решаются довольно сложно, однако будучи поставлены в частное положение, решаются легко. Примером может служить одна из основных задач курса: определение расстояния от точки до прямой. Сущность методов преобразования чертежа состоит в том, что задача общего положения переводится в частное, где она решается значительно легче. Будем рассматривать следующие методы преобразования чертежа: 1. Метод перемены плоскостей проекций 2. Метод вращения ЛЕКЦИЯ 6 МЕТОД ВРАЩЕНИЯ
Сущность метода вращения состоит в том, что при фиксированном положении плоскостей проекций будем вращать геометрические элементы задачи до такого положения, в котором задача могла бы быть решена легко. При вращении вокруг неподвижной оси каждая точка вращаемой фигуры перемещается в плоскости, перпендикулярной к оси вращения, точка перемещается по окружности, центр которой лежит на оси вращения, а радиус равен расстоянию от точки до оси. Все точки фигуры должны поворачиваться вокруг одной оси в одну и ту же сторону, на один и тот же угол. Точки, находящиеся на оси вращения, остаются неподвижными. Наиболее просто задача решается, если ось вращения перпендикулярна или параллельна плоскости проекций.
ЛЕКЦИЯ 7 7.1. ГРАННЫЕ ПОВЕРХНОСТИ И МНОГОГРАННИКИ.
Гранные поверхности образуются перемещением прямолинейной образующей ℓ по ломаной направляющей m. При этом, если одна точка S образующей неподвижна, получается парамидальная поверхность, если же при перемещении образующая параллельна заданному направлению, то создается призматическая поверхность (рис.1).
Элементами гранных поверхностей являются: вершина S (у призматических поверхностей она находится в бесконечности), грань (часть плоскости, ограниченная одним участком направляющей m и крайними относительно его положениями образующей ℓ), ребро (линия пересечения смежных граней). Определитель пирамидальной поверхности включает в себя вершину S, через которую проходят образующие, и направляющую: S Определитель призматической поверхности содержит направление n, которому параллельны все образующие ℓ поверхности: ℓ║n, ℓ∩m. Замкнутые гранные поверхности, образованные некоторым числом (не менее четырех) граней, называются многогранниками. Из числа многогранников выделяют группу правильных многогранников, у которых все грани правильные и равные многоугольники, а многогранные углы при вершинах выпуклые и содержат одинаковое число граней. Например, тетраэдр – правильный четырехгранник, а гексаэдр – куб, октаэдр – многогранник. Пирамида – многогранник, в основании которого лежит произвольный многоугольник, а боковые грани – треугольники с общей вершиной S. На комплексном чертеже пирамида задается проекциями ее вершин и ребер. Видимость ребер определяется с помощью конкурирующих точек (рис.2).
Призма – многогранник, у которого основания – два одинаковых и взаимно параллельных многоугольника, а боковые грани – параллелограммы. Если ребра призмы перпендикулярны плоскости основания, то такую призму называют прямой (рис.3).
ЛЕКЦИЯ 1 МЕТОД ПРОЕЦИРОВАНИЯ ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

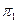 (рис.1).
(рис.1).
 А
А 
 и плоскости проекций (рис.2).
и плоскости проекций (рис.2).


 – вертикально. Плоскость
– вертикально. Плоскость 
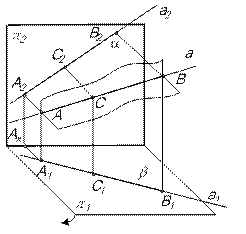
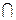 [АА1]) перпендикулярную плоскостям проекций и линии их пересечения – оси ОХ. Эта плоскость пересекает
[АА1]) перпендикулярную плоскостям проекций и линии их пересечения – оси ОХ. Эта плоскость пересекает 



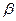 ([АА1] || [ВВ1]) ∩
([АА1] || [ВВ1]) ∩ 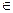 [А1В1]; C2
[А1В1]; C2 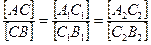 .
.


 называется профильной прямой (рис.6). d2
называется профильной прямой (рис.6). d2  OX, d1
OX, d1 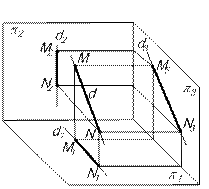
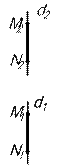
 В1
В1 
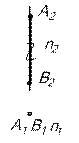

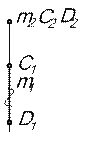
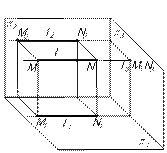
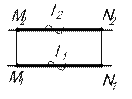
 (рис.10).
(рис.10).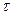 (рис.11).
(рис.11).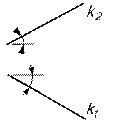
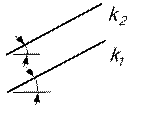

 ([ВВ1]∩[ВС]), но АВ║А1В1 – поэтому А1В1
([ВВ1]∩[ВС]), но АВ║А1В1 – поэтому А1В1 





 =
=  , который образуется между плоскостью
, который образуется между плоскостью 

 =
= 



















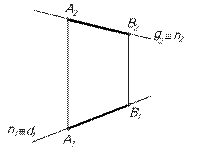
 = а
= а  ∩
∩  = b
= b  ∩
∩  =n; n1
=n; n1 



 =m;
=m;  ∩
∩  ;
;  ;
;  =L1;L2
=L1;L2 










