
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к выполнению контрольно-графической работы № 1.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кремлева Людмила Викторовна
Методические указания
по дисциплине
«Инженерная графика»
Часть 1 «Основы начертательной геометрии»
Северодвинск ВВЕДЕНИЕ Начертательная геометрия и техническое черчение входят в число дисциплин, составляющих основу инженерного образования. Курс начертательной геометрии сводится к изложению методов решения различных геометрических задач, графическими методами. Студент должен самостоятельно наметить ход решения каждой задачи и дать ему нужное графическое оформление. Необходимые навыки приобретаются в процессе самостоятельной работы. Настоящее пособие содержит материал, необходимый при подготовке к практическим занятиям, выполнению самостоятельных заданий и контрольно-графической работы № 1 по разделу «Начертательная геометрия» дисциплины "Начертательная геометрия и инженерная графика". для студентов 1 курса заочного отделения специальности 140200. Поскольку все задачи решаются графически, оформление должно быть тщательным. Степень точности решения задач определяется точностью графических построений. В настоящем методическом отражены те разделы начертательной геометрии, которые предусмотрены учебной программой курса «Начертательная геометрия» дисциплины "Начертательная геометрия и инженерная графика". В разделах 2-8 содержатся основные теоретические положения, примеры решения задач и задачи для самостоятельного решения по наиболее важным разделам начертательной геометрии. В разделе 1 приведены методические указания, варианты заданий контрольно-графической работы № 1. В приложении приведен пример выполнения работы.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНО-ГРАФИЧЕСКОЙ РАБОТЫ № 1 И ЗАДАЧ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ Методические указания к выполнению контрольно-графической работы № 1. Контрольно-графическая работа № 1 состоит из двух эпюров (чертежей). Эпюры выполняются на стандартных форматах чертежной бумаги: эпюр № 1 – на формате A4, эпюр № 2 – на формате A3. Каждый эпюр должен иметь стандартную рамку рамку и основную надпись по форме 1 Гост 2.104-68 [см. 7]. В графе “Обозначение” основной надписи подписать РГ XX.03 шрифтом № 10, где НЧ - тема задания (начертательная геометрия), XX - номер варианта задания, 01 или 02 - номер эпюра по порядку. В графе “Наименование” основной надписи подписать «Эпюр № 1 (или № 2)».
Эпюр № 1 должен содержать решение 2-х задач по темам «Точка, прямая, плоскость». Обе задачи решаются на одном чертеже. Эпюр № 2 – решение задачи по теме «Сечение поверхности плоскостями общего положения».
Варианты заданий к эпюру № 1. Задача 1. Определить расстояние от точки D до плоскости a, заданной треугольником ABC и видимость перпендикуляр по отношению к плоскости. Все точки заданы в координатном виде (табл. 1). Задача 2. Построить плоскость b, параллельную плоскости a (плоскость из задачи № 1) и удаленную от нее на 50 мм. Таблица 1
Решение задач осуществляется в следующем порядке: 1. Построить на эпюре точки A, B, C и D по их координатам. 2. Соединить точки A, B, C в треугольник. 3. Опустить на плоскость a (D ABC) перпендикуляр. 4. Найти точку K – точку пересечения перпендикуляр и плоскости. 5. Методом прямоугольного треугольника определить натуральную величину отрезка DK 6. Методом конкурирующих точек определить видимость перпендикуляра по отношению к плоскости. 7. В плоскости a (D ABC) выбрать произвольную точку, например C. 8. Из выбранной точки восстановить перпендикуляр к плоскости. 9. Отложить от выбранной точки вдоль перпендикуляра отрезок длиной 50 мм, конец отрезка обозначить. 10. Через точку L провести плоскость b (в виде пересекающихся прямых), параллельную a (D ABC). Пример выполнения эпюра № 1 приведен в Приложении.
Варианты заданий к эпюру № 2 Условие задачи. Построить отсеченную часть комбинированного тела в трех проекциях и натуральную величину сечения.
Варианты заданий к эпюру № 2.
Решение задачи осуществляется в соответствии с разделом 7 настоящего пособия. Пример выполнения эпюра № 2 приведен в Приложении.
ОСНОВНЫЕ ПОНЯТИЯ МЕТОДА ПРОЕКЦИЙ
Основные понятия метода проекций как основы для получения изображений на чертежах. К основные формообразующим элементам пространства относятся точка, прямая и плоскость. Ими определяются простые трехмерные фигуры, из которых создаются более сложные пространственные объекты. Между элементами пространства существуют следующие отношения: тождественность (совпадение) - º; инцидентность (принадлежность) - Î; параллельность - êê; перпендикулярность - ^. Над элементами пространства можно выполнять операции объединения - È - и пересечения - Ç. Изображения объектов трехмерного пространства на плоскости получают методом проецирования. Аппарат проецирования включает в себя проецирующие лучи, проецируемый объект (оригинал) и плоскость, на которой получается изображение. Все лучи, проецирующие предмет, исходят из одной точки, называемой центром проекций. Если точка находится на определенном расстоянии от плоскости проекций, то такое проецирование называется центральным. Если центр проекций удален в бесконечность, то все лучи становятся параллельными и проецирование называется параллельным. Параллельное проецирование является косоугольным, если проецирующие лучи наклонены к плоскости проекций под углом, отличным от прямого. В противном случае проецирование является – ортогональным. Основные свойства проекций. 1. Проекция точки есть точка. 2. Проекция прямой есть прямая. При параллельном проецировании проекции параллельных прямых есть параллельные прямые. 3. Проекцией плоскости является плоскость проекций. 4. При ортогональном проецировании длина проекции отрезка меньше либо (в частном случае) равна длине самого отрезка. Проецированием на одну плоскость проекций получается изображение, которое не позволяет однозначно определить его форму и размеры. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, т.к. по такому чертежу невозможно воспроизвести оригинал. На практике применяют различные способы дополнения однопроекционного чертежа. В курсе начертательной геометрии главным образом рассматриваются чертежи, получаемые ортогональным проецирование на две или более взаимноперпендикулярные плоскости проекций (комлексные чертежи или эпюры). Другим способом получение обратимого чертежа является перепроецирование вспомогательной проекции предмета на основную аксонометрическую плоскость проекций - аксонометрические чертежи, способы получения которых в данном пособии не рассматриваются.
ЭПЮР ТОЧКИ
Пример решения задачи на построение эпюра точки Построить ортогональные (эпюр, двухпроекционный чертеж) и аксонометрические проекции точек А (30,-18,30) и B (15,25, 50), а также: - точки K, симметричной точке А относительно плоскости p1; - точки С, симметричной точке A относительно плоскости p2; - точки D, симметричной т. B относительно оси OX; Аксонометрические проекции точек следует строить во фронтальной диметрической проекции – ГОСТ 2.317-69.
Решение Для построения на эпюре точки А проведем ось OX. От точки О откладываем координату xA, полученную точку обозначаем Ax (рис.3.4). Через точку Ax проводим линию связи, перпендикулярную оси OX. Вдоль линии связи откладываем координаты zA=30 мм – выше оси OX (т.к. значение положительно), yA=18 мм выше оси OX (т.к. значение y отрицательно). В результате координата zAопределит положение фронтальной проекции А2 точки А, а yA – горизонтальной проекции A1. Для построения аксонометрической проекции точки А нужно известные координаты отложить вдоль соответствующих осей и далее выполнять построения, очевидные по рис.3.4. Так как в качестве аксонометрической выбрана прямоугольная диметрия, то координата y при построениях уменьшается вдвое.
Рис.3.4
Для определения искомых координат точек, симметричных относительно геометрических объектов заданным, удобно использовать аксонометрическое изображение плоскостей p1/p2 под другим углом зрения (рис.5) (вдоль оси OX, ось OX направлена на нас). На рис.3.5, например, можно видеть построение точки D, симметричной т.B относительно оси OX. Подобное представление удобно для установления связи координат искомых точек К,С, D и М, необходимых для построения их эпюров. xK=xА, yK=yA, zK=-zA; xС=xА, yС=-yA, zС=zA; (1) xD=xВ, yD=-yВ, zD=-zВ; В истинности выражений (1) предлагается убедиться самостоятельно.
Рис.3.5
3.3.Задачи для самостоятельного решения по теме «Эпюр точки» Задача 1. Определить по эпюру координаты точек в мм, определить положение точек относительно плоскостей проекций (указать угловой квадрант), построить третьи проекции точек (рис.3.6).
Задача 2. Построить эпюр и аксонометрию (прямоугольную диметрию) проекции точек А (15, -55, 48) и В (50,-10,-37).
Задача 3. Точка А имеет координаты (30,25,-34). Требуется построить: - точку В, симметричную точке А относительно p1; - точку С, симметричную точке А относительно p2; - точку Е, симметричную точке А относительно p3.
Рис.3.6
Задача 5. По заданным проекциям точки А построить ось проекций OZ (рис.2.7). Рис.3.7
Задача 6. Дать ответы на следующие вопросы: 1. Каково условие принадлежности точки плоскости p1? 2. Какой координатой определяется расстояние от точки до плоскости p1,p2, p3? 3. Каково условие принадлежности точки оси OY? 4. К какой из плоскостей находится ближе всего точка А (70,64,-12)? 5. Какими координатами определяется фронтальная проекция точки? 6. Какими координатами определяется горизонтальная проекция точки проекция точки? 7. При каком условии точка будет равноудалена от плоскостей проекций p1p2p3?
Примеры решения задач Задача 1. Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прямоугольного треугольника).
Рис.4.3
Строим прямоугольный треугольник, взяв за один катет горизонтальную (или фронтальную) проекцию отрезка - проекцию А1В1 (рис.4.3), а за другой – разность удалений концов отрезка от горизонтальной плоскости проекций Dz=zВ-zА (или соответственно от фронтальной плоскости проекций - Dy=yВ-yА). Величину Dz можно определить, проведя вспомогательную линию через один из концов отрезка перпендикулярно линии связи. Гипотенуза прямоугольного треугольного треугольника А1В1Во и будет равна истинной величине отрезка АВ. Угол между гипотенузой и катетом, равным горизонтальной проекции отрезка, определяет величину угла наклона j заданного отрезка к горизонтальной плоскости проекций. Для определения угла наклона y к фронтальной плоскости проекций необходимо еще раз построить истинную величину отрезка с помощью прямоугольного треугольника А2А0В2. При этом |А0А2|=|А1В0|. Если по условию задачи требуется определить только истинную величину отрезка прямой, достаточно построить прямоугольник на одной из проекций.
Задача 2. Разделить отрезок АВ точкой С в отношении 2:3 (рис.4.4).
Дано: Решение:
Рис.4.4
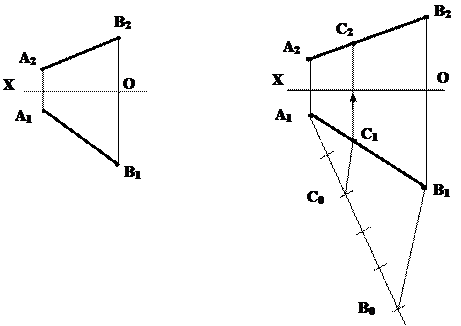
Для того, чтобы построить точку С, делящую отрезок в заданном отношении, достаточно одну из проекций отрезка (на рис. 4.4) горизонтальная проекция) разделить в этом отношении, а затем построить вторую проекцию искомой точки, используя линию связи. Деление проекции А1В1 произведено с помощью теоремы Фалеса. Для этого из любого конца проекции А1В1, например из точки А1 проводим луч под произвольным углом, на котором откладываем 2+3=5 равных отрезков произвольной длины. Соединяем точки В0В1, затем проводим через С0 прямую С0С1||B0B1. Задача 3. Достроить отрезок АВ, если длина его равна 50 мм (рис.4.5). Задача является обратной к определению истинной величины отрезка прямой.
Рис.4.5
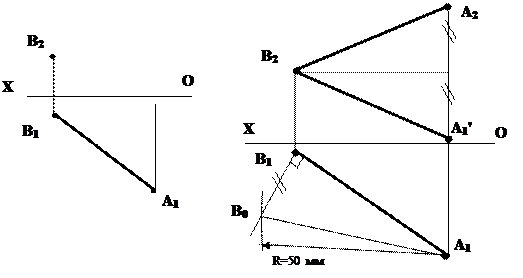
Для того, чтобы достроить фронтальную проекцию точки A(A2) необходимо знать разность удалений концов отрезка АВ от плоскости p1: Dz=zВ-zА, значение которой можно узнать, построив прямоугольной треугольник, взяв за один из катетов известную горизонтальную проекцию отрезка АВ. Треугольник построен по известному катету и гипотенузе (известной истинной величине отрезка АВ). Из прямоугольного треугольника А1В1В0 находим, что Dz=|В1В0|. Задача имеет два решения (две точки A2 и A'2).
Задача 4. На прямой a (a1,a2) от точки А отложить отрезок АС, длиной 30 мм (рис.34.6). Дано: Решение:
Рис.4.6 На прямой а зададимся произвольным отрезком АВ. С помощью прямоугольного треугольника А1В1В0 определим истинную величину отрезка АВ. Далее от точки А1 откладываем вдоль гипотенузы заданный отрезок 30 мм. Определяем искомую точку С(С1,С2), используя положение о пропорциональности деления отрезка, при этом С0С1||В0В1.
Задача 5. (Задача на профильные прямые). Достроить прямую NM, параллельную прямой КL (рис.4.7). Замечание. Задачи на профильные прямые могут быть решены различными методами, в частности, с помощью построения третьей проекции этих прямых, либо с помощью методов косоугольного параллельного проецирования путем построения, так называемых, вспомогательных прямых. К этому типу задач следует отнести задача по определению взаимного положения профильных прямых, построения точки пересечения профильных прямых, а также ряд позиционных задач, связанных с построением точек пересечения профильной прямой и плоскости. Приведем решение задачи на профильные прямые методом построения вспомогательных прямых.
Дано: Решение:
Рис.4.7 Для того, чтобы построить недостающую фронтальную проекцию N2 точки N, воспользуемся методом вспомогательных прямых. Суть его заключается в следующем. Для исходных профильных прямых методом косоугольного проектирования строятся вспомогательные прямые. По взаимному положению вспомогательных прямых судят о взаимном положении соответствующих им профильных прямых: если вспомогательные прямые параллельны, то параллельны соответствующие профильные прямые, если вспомогательные пересекаются, то исходные прямые или пересекаются или скрещиваются. Построим вспомогательную прямую для прямой KL. Для этого из точек K1 и K2 проведем лучи произвольного направления до пересечения в точке K0. Точка К0 – является вспомогательной для точки К. Аналогично строим точку L0 – вспомогательную для точки L. При этом [L1L0)|| [K1K0), [L2L0)|| [K2K0). Прямая К0L0 является вспомогательной для прямой KL. Так как точка M, принадлежащая второй профильной прямой определена однозначно (известны обе ее проекции), построим вспомогательную ей точку М0, при построении которой должна быть соблюдена параллельность проецирующих лучей на соответствующих проекциях: [М1М0)|| [K1K0)|| [L1L0) и [М2М0)|| [K2K0)|| [L2L0). Так как исходные прямые должны быть параллельны, поэтому через построенную точку М0 зададим направление вспомогательной прямой М0N0, параллельно прямой K0L0. Для нахождения точки L0 проведем проецирующий луч из точки L1, параллельно лучам на горизонтальной проекции до пересечения с прямой, проведенной из точки M0. Точка пересечения L0будет являться вспомогательной для точки L, с помощью которой отыскивается неизвестная фронтальная проекция L2 точки L.
4.3. Задачи для самостоятельного решения Задача 1. Достроить недостающую проекцию точки С, принадлежащей отрезку АВ, а также определить истинную величину отрезка АВ и углы его на клона к плоскостям проекций (рис.4.8).
Рис. 4.8
Задача 2. Построить на эпюре и в аксонометрии изображение прямой, проходящей через точки А(50,40,10) и В(25,10,30). Определить истинную величину отрезка АВ.
Задача 3. Определить относительное положение прямой а и точек А, В, С и D (рис.4.9).
Рис.4.9 Задача 4. Определить взаимное положение прямых а и b (рис.4.10).
Рис.4.10
Задача 5. Задана прямая m||p1. На расстоянии 30 мм от m построить прямую n||m. (При решении использовать теорему о проецировании прямого угла)(рис.4.11).
Рис.4.11
Задача 6. Через точку С провести прямую, параллельную отрезку АВ (рис.3.12).
а) б) Рис.4.12
Задача 7. Достроить проекции треугольника АВС, если истинная величина сторон АВ=60 мм, ВС=50 мм. Определить угол наклона стороны АС к плоскости p1 (рис.4.13).
Рис.4.13
ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ
Примеры решения задач Задача 1. Достроить плоский четырехугольник (рис.5.4).
Дано: Решение: Рис.5.4 Решение задачи сводится к построению недостающей проекции точки D, принадлежащей плоскости, заданной точками А,В,C. Зададим эту плоскость треугольником АВC, для чего соединим точки В и C прямой линией на обеих проекциях. Проведем фронтальную проекцию диагонали четырехугольника А2D2. Затем достроим вторую ее проекцию, для чего из точки пересечения фронтальных проекций диагоналей (точка О2) опустим линию проекционной связи на прямую D1C1. Прямая А1О1 задаст направление диагонали четырехугольника на горизонтальной проекции. Пересекаем Прямую А1О1 с соответствующей линией связи (из D2), получаем искомую проекцию точки С. Точка С принадлежит плоскости треугольника АВС, т.к. принадлежит прямой АО, лежащей в этой плоскости. Прямая принадлежит плоскости треугольника АВС, т.к. имеет с ней две общие точки (А и О). Следовательно, достроенный четырехугольник – плоский.
Рис.5.5
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости. Через известную проекцию точки А - точку А1- проводим произвольную прямую. Строим вторую проекцию введенной прямой, которая должна лежать в заданной плоскости. Для этого фиксируем точки пересечения 12 и 22 со сторонами треугольника В2D2 и C2D2. Отыскиваем горизонтальные проекции точек 1 и 2 на соответствующих сторонах горизонтальной проекции треугольника ВСD. Строим горизонтальную проекцию прямой 12 (1121), пересечение которой с линией связи из точки А2, определит искомую проекцию точки А.
Задача 3. Через заданную точку Е с помощью главных линий построить плоскость b(hÇf) параллельно заданной плоскости a(a||b). Построенную плоскость задать параллельными прямыми (рис.5.6). Дано:
Решение:
Рис.5.6
Построим вначале главные линии плоскости a. Построение главных линий начинают с проведения тех проекции, направление которых всегда известно (у горизонтали - это ее фронтальная проекция h'2||OX; у фронтали - ее горизонтальная проекция f''1||OX). На рис. 5.6 главные линии плоскости проведены через точку А, произвольно выбранной в плоскости a. Проведя затем через точку E параллельные прямые (h'2||h2 и f''1|| f'1), найдем искомую плоскость b(hÇf) || a(a||b). Для того, чтобы перезадать плоскость b(hÇf) параллельными прямыми, достаточно через любую точку плоскости, например, через выбранную произвольно точку К, провести прямую m, параллельно любой прямой, лежащей в этой плоскости (в данном примере m||f, при этом m1||f1 и m2||f2). Плоскость b теперь задана параллельными прямыми m||f. Задача 4. Построить линию пересечения двух плоскостей: плоскости общего положения a(aÇb) и фронтально-проецирующей плоскости b(b2)(рис.5.7). Дано: Решение:
Рис.5.7 Линия пересечения двух плоскостей в данном случае определяется двумя точками пересечения следа фронтально-проецирующей плоскости b2 с двумя прямыми а и с в плоскости a. При этом прямая с(с1,с2) - дополнительная, проведенная произвольно в плоскости, но так, чтобы точка К линии пересечения получилась в поле заданного чертежа. Точки К и L являются общими для двух заданный плоскостей, а, следовательно, и определяют искомую линию пересечения: (КL)= a(aÇb) Ç b(b2).
Задача 5. Построить линию пересечения двух плоскостей общего положения: a(DАВС) и b(а||b)(рис.5.8).
Дано:
Решение:
Рис. 5.8
При решении этой задачи используется метод секущих плоскостей. Так как две плоскости пересекаются по прямой линии, определяемой двумя точками, для построения необходимо ввести две дополнительные секущие плоскости. Порядок решения задачи: 1. Вводим дополнительную секущую плоскость d(d2). В качестве секущей плоскости выбрана фронтально-проецирующая плоскость, заданная своим следом на фронтальной плоскости проекций. (В качестве секущей плоскости может быть выбрана произвольная проецирующая плоскость). 2. Строим линию пересечения фронтально-проецирующей плоскости d(d2) с плоскостью общего положения a(DАВС) (см.пример 4): 12(1121;1221)= d(d2) Ça(DАВС). 3. Строим линию пересечения фронтально-проецирующей плоскости d(d2) с плоскостью общего положения b(а||b): 34(3141;3242)= d(d2) Çb(а||b). 4. Строим точку М как точку пересечения прямых 12 и 34: М1=1121 Ç3141 Вторая проекция точки М точка М2, отыскивается на следе вспомогательной секущей плоскости d(d2) с помощью лини проекционной связи. Точка М является искомой точкой, поскольку принадлежит одновременно трем плоскостям: вспомогательной d(d2) и заданных a(DАВС) и b(а||b), и, следовательно, является точкой, принадлежащей линии пересечения двух исходных плоскостей. 5. Аналогично строится вторая точка, принадлежащая линии пересечения N. Для этого вводится еще одна вспомогательная секущая плоскость g(g2). Плоскость g(g2) также является фронтально-проецирующей плоскостью, кроме того, параллельной плоскости d(d2). Это является необязательным, поскольку вспомогательные плоскости могут быть выбраны совершенно произвольно. 6. После построения точки N проводим прямую MN, которая является искомой линией пересечения двух исходных плоскостей.
Задача 6. Построить линию пересечения двух плоскостей общего положения a(DАВС) и b(DDEF) (рис.5.9). Дано:
Решение:
Рис. 5.9 (продолжение)
Задача решается аналогично предыдущей. Для уменьшения количества вспомогательных построений в качестве секущих введены плоскости d(d2) и g(g2) через прямые, принадлежащие одной из плоскостей (DE и DF), следы секущий плоскостей совпадают соответствующими проекциями этих прямых.
5.3. Задачи для самостоятельного решения Задача 1. Достроить плоский пятиугольник (рис.5.10).
Рис.5.10
Задача 2. Достроить недостающую проекцию прямой а, лежащей в плоскостях: d(c||d) (рис.45.11).
Рис.5.11
Задача 3. Достроить точку А, принадлежащую плоскостям: а) a(aÇc); б) d(c||d) (рис.4.12).
а) б) Рис.5.12 Задача 4. В плоскости a(АВС) провести горизонталь и фронталь.
Рис.5.13
Задача 5. Построить линии пересечения двух плоскостей (рис.4.14).
Рис.5.14
Примеры решения задач Задача 1. Найти точку пересечения прямой m(rn1, m2) с плоскостью треугольника АВС {рис.6.1). Определить видимость, прямой относительно заданной плоскости.
Дано: Решение:
Рис.6.1
Через прямую m строится вспомогательная фронтально-проецирующая плоскость b(b2) (можно взять и горизонтально-проецирующую плоскость). В этом случае следна эпюребудет совмещен с проекцией прямой m2. Далее строится линия пересечения 1 2=bÇa, положениекоторой определится точками 1 и 2, полученными от пересечения следа b2, со сторонами треугольника. Точка пересечения построенной линии с заданной прямой К=12Çm и будетискомой точкой встречи. Для определения видимости выбирается по паре конкурирующих точек на каждой проекции чертежа, например, точки 1, 3 конкурируют относительно p2. Точка 1 (точка, принадлежащая плоскости) ближе к нам, так как дальше удалена от p2 , поэтому она и с ней отрезок АС (1ÎАС) закрывают прямую m, часть которой 3 К будет невидима на фронтальной проекции. В точке пересечения прямой и плоскости видимость сменится и после точки К2 на фронтальной проекции прямая будет видима. Аналогично определяют видимость прямой и плоскости относительно p1, используя, например, конкурирующие точки 4-5.
Задача 2. Построить перпендикуляр к плоскости a(с||d) длиной 30мм (рис.6.2).
Дано: Решение:
Рис.6.2
Для восстановления перпендикуляра к плоскости нужно построить главныелинии плоскости - горизонталь h(h1,h2) и фронталь f(f1,f2). Перпендикуляр l к плоскостиможно восстанавливатьиз любойее точки, например, из точки К(К1К2) - точки пересечения горизонтали и фронтали К=hÇf при этом, l1^h1 и l2^h2. Для того, чтобы отложить на отрезке l заданную длину 30 мм, первоначально задаются произвольной отрезком К5 (точка 5 выбирается произвольно на перпендикуляре l), определяют его натуральную величину помощью треугольника K15150. После этого от точки К1 вдоль К150 откладывают заданную длину перпендикуляра и отыскивают проекцию L1. С помощью линий проекционной связи отыскивают вторую проекцию точки L2: l(K1L1, K2L2) ^a.
Задача 3. Определить расстояние от точки А до плоскости a(a||b) (рис.6.3).
Дано: Решение:
Рис.6.3. Задача решается в три этапа: 1) из точки А задать направление перпендикуляра к плоскости с помощью главных линий плоскости; 2) найти точку пересечения перпендикуляра и плоскости (пример1). 3) с помощью прямоугольного треугольника определяем истинную величину отрезка перпендикуляра между заданной плоскостью и точкой встречи перпендикуляра и плоскости. Истинная величина этого отрезка – искомое расстояние между точкой и плоскостью. Задача 4. Через точку р(р1Р2) Îm(m1,m2) построить плоскость, перпендикулярную прямой m (рис.6.4). Дано: Решение:
Рис..6.4.
Через точку Р нуж но провести фронталь f и горизонталь h так, чтобы h1^m1, h2^m2. В этом случае прямая m будет перпендикулярна плоскости, заданной пересекающимися главными линиями m ^b(hÇf).
6.3.Задачи для самостоятельного решения Задача 1. По данной фронтальной проекции прямой а, параллельной плоскости треугольника АВС, построить ее горизонтальную проекцию (рис.6.5).
Рис.6.5 Задача 2. Через точку С построить плоскость, параллельную заданной прямой a. Плоскость задать треугольником (рис.6.6).
Рис.6.6 Задача 6. Найти точку пересечения прямой АВ и плоскости,определить видимость прямой относительно плоскости.
Рис.6.7
Примеры решения задач. Задача 1. Построить сечение пирамиды SABCD заданной горизонтально-проецирующей плоскостью a(a2) и определить натуральную величину сечения методом перемены плоскостей проекций (рис.7.3).
Искомое сечение – пятиугольник 12344', вершины которого на эпюре определяются точками пересечения следа плоскости a(a2) с ребрами пирамиды. Натуральную величину сечения можно определить методом перемены плоскостей проекций, для чего проводим новую ось плоскостей проекций параллельно следу секущей плоскости.
Задача 2. Построить сечение конуса фронтально-проецирующей плоскостью в трех проекциях (рис.7.4).
Секущая плоскость пересекает две образующие конуса, поэтому в сечении получится эллипс (часть его). Характерные точки сечения получатся в результате пересечения очерковой образующей конуса со следом секущей плоскости (точка 1), и окружностью основания. Дополнительные точки сечения можно получить, выбрав ряд точек, принадлежащих следу секущей плоскости, построив их затем на поверхности конуса с помощью образующих или с помощью параллелей. Для эллипса сечения необходимо также определить положение его осей.
Рис.7.4 Задача 3. Построить в трех проекциях геометрическое тело с вырезом части (рис.7.5). Дано: Решение:
При решении задач подобного типа необходимо предварительно проанализировать вид секущих плоскостей. Если вырез строится для гранного тела, то необходимо строить точки пересечения следов секущих плоскостей с ребрами гранного тела, а также точки пресечения следов секущих плоскостей между собой (эти точки обычно принадлежат граням тела). Для удобства построения точки желательно пронумеровать по порядку. После построения точек, принадлежащих либо граням, либо ребрам тела на всех проекциях, точки соединяют в необходимой последовательности прямыми линиями. После этого необходимо оформить чертеж окончательно, учитывая видимость и невидимость вновь образованных ребер. Если вырез строится для тела вращения, необходимо выяснить, какая кривая будет являться результатом сечения той или иной плоскостью заданного тела. Необходимо прежде всего строить точки пересечения следов секущих плоскостей, а затем ряд дополнительных точек, принадлежащих следам. После построения выбранных точек на всех проекциях, их плавно соединяют. Затем необходимо окончательно оформить чертеж, учитывая видимость вновь образованных ребер (рис.7.6). Дано: Решение:

Рис.7.6. 7.3.Задачи для самостоятельного решения
Рис.7.7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 2135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.164 (0.012 с.) |

















 Задача 2. Достроить точку А, если она принадлежит плоскости D ВСD (рис.5.5). Дано: Решение:
Задача 2. Достроить точку А, если она принадлежит плоскости D ВСD (рис.5.5). Дано: Решение:




 Рис.5.9
Рис.5.9


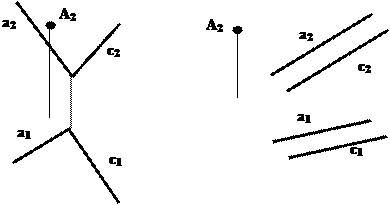


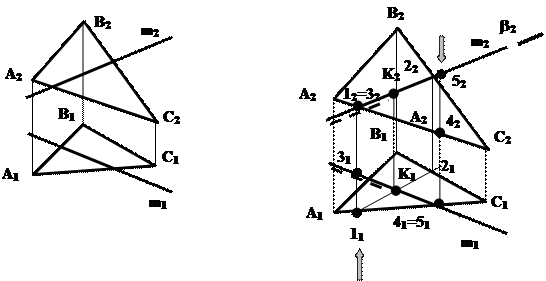





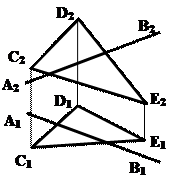
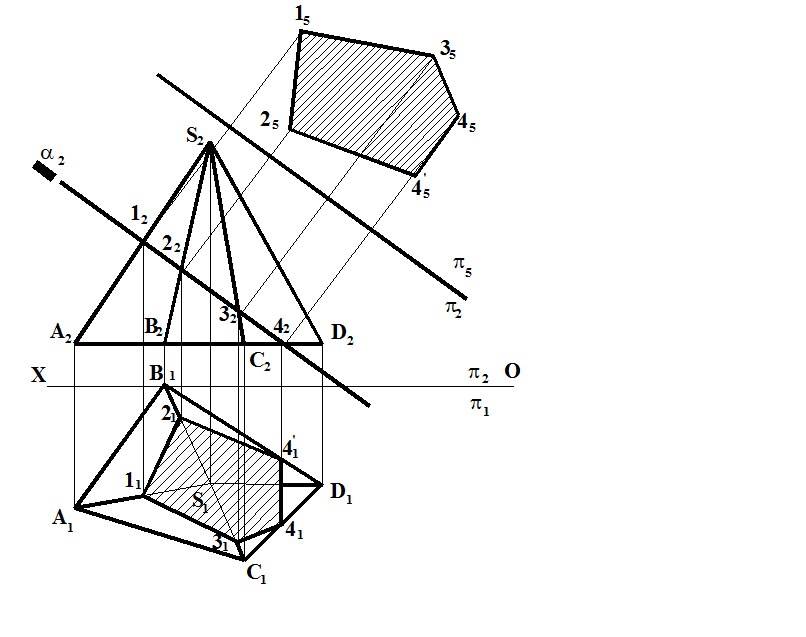 Рис.7.3
Рис.7.3

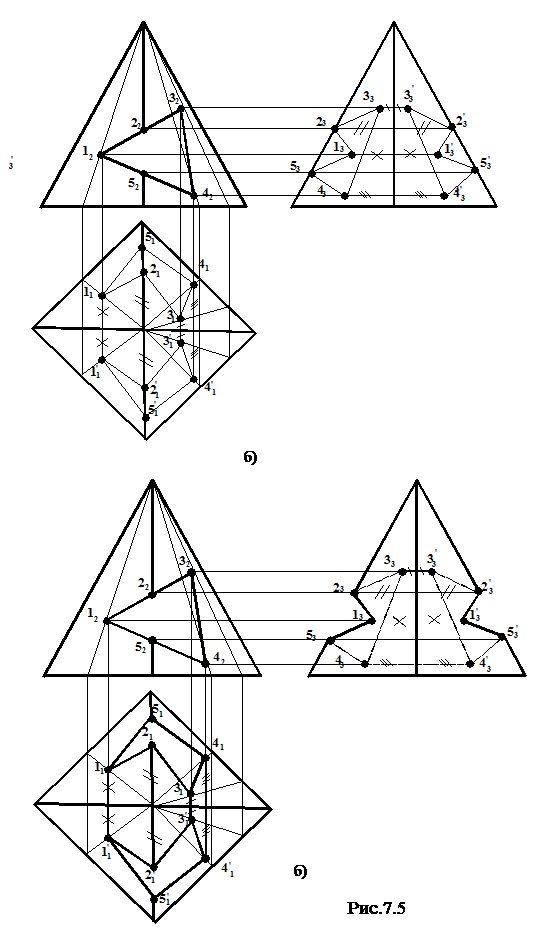


 Задача 2. Построить отсеченную часть геометрическ
Задача 2. Построить отсеченную часть геометрическ 


