Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхности. Сечение поверхностей плоскостями частного положенияСодержание книги
Похожие статьи вашей тематики
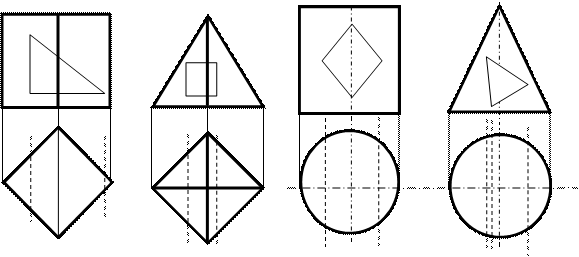
Поиск на нашем сайте Основные теоретические положения. Поверхность представляет собой множество последовательных положений линии, перемещающейся в пространстве. Эту линию называют образующей. Закон перемещения образующей может быть задан тоже линиями. Эти линии называются направляющими. Гранные поверхности образуются перемещением прямолинейной образующей L по ломаной направляющей. Поверхности вращения образуются вращением образующей L вокруг прямой i - оси вращения, при этом направляющими обычно являются окружностями. Вид поверхности зависит от формы образующей линии и от закона перемещения ее в пространстве вдоль направляющей. Точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку (рис.7.1).
Рис.7.1
Каждая точка образующей поверхности вращения описывает окружность, плоскость которой перпендикулярна оси вращения. Такие окружности называются параллелями. Кривые на поверхности вращения, образующиеся в результате пересечения поверхности вращения плоскостями, проходящими через ось вращения, называются меридианами. Строить точки на поверхности вращения удобнее всего с помощью параллелей (рис.7.2).
Рис.7.2 Линия сечения поверхности проецирующей плоскостью строится по точкам пересечения образующих поверхности или ее параллелей с плоскостью. Для гранных тел линией сечения будет ломаная, построенная на эпюре по точкам пересечения следа проецирующей плоскости с ребрами гранной поверхности. Если даны тела вращения, то для решения задачи нужно выбрать несколько, принадлежащих следу секущей плоскости, точек, провести через выбранные точки параллели (или образующие), определить точки пересечения их со следом секущей плоскости; построить по ним лекальную кривую сечения. При этом в первую очередь следует определить характерные точки линии сечения на очерковых образующих (наиболее близкие, наиболее удаленные и др.).
Примеры решения задач. Задача 1. Построить сечение пирамиды SABCD заданной горизонтально-проецирующей плоскостью a(a2) и определить натуральную величину сечения методом перемены плоскостей проекций (рис.7.3).
Искомое сечение – пятиугольник 12344', вершины которого на эпюре определяются точками пересечения следа плоскости a(a2) с ребрами пирамиды. Натуральную величину сечения можно определить методом перемены плоскостей проекций, для чего проводим новую ось плоскостей проекций параллельно следу секущей плоскости.
Задача 2. Построить сечение конуса фронтально-проецирующей плоскостью в трех проекциях (рис.7.4).
Секущая плоскость пересекает две образующие конуса, поэтому в сечении получится эллипс (часть его). Характерные точки сечения получатся в результате пересечения очерковой образующей конуса со следом секущей плоскости (точка 1), и окружностью основания. Дополнительные точки сечения можно получить, выбрав ряд точек, принадлежащих следу секущей плоскости, построив их затем на поверхности конуса с помощью образующих или с помощью параллелей. Для эллипса сечения необходимо также определить положение его осей.
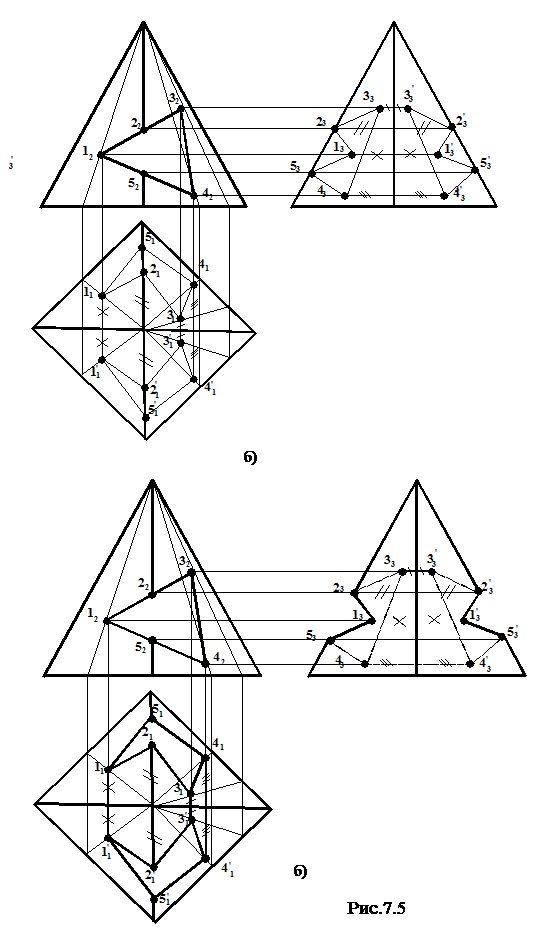
Рис.7.4 Задача 3. Построить в трех проекциях геометрическое тело с вырезом части (рис.7.5). Дано: Решение:
При решении задач подобного типа необходимо предварительно проанализировать вид секущих плоскостей. Если вырез строится для гранного тела, то необходимо строить точки пересечения следов секущих плоскостей с ребрами гранного тела, а также точки пресечения следов секущих плоскостей между собой (эти точки обычно принадлежат граням тела). Для удобства построения точки желательно пронумеровать по порядку. После построения точек, принадлежащих либо граням, либо ребрам тела на всех проекциях, точки соединяют в необходимой последовательности прямыми линиями. После этого необходимо оформить чертеж окончательно, учитывая видимость и невидимость вновь образованных ребер. Если вырез строится для тела вращения, необходимо выяснить, какая кривая будет являться результатом сечения той или иной плоскостью заданного тела. Необходимо прежде всего строить точки пересечения следов секущих плоскостей, а затем ряд дополнительных точек, принадлежащих следам. После построения выбранных точек на всех проекциях, их плавно соединяют. Затем необходимо окончательно оформить чертеж, учитывая видимость вновь образованных ребер (рис.7.6). Дано: Решение:

Рис.7.6. 7.3.Задачи для самостоятельного решения
Рис.7.7
Рис. 7.8
Задача 3. Построить геометрическое тело в трех проекциях (рис.6.9).
Рис.79
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


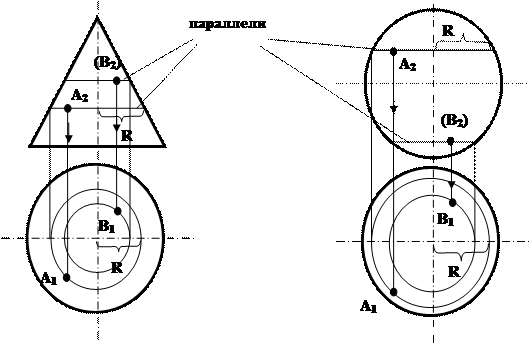
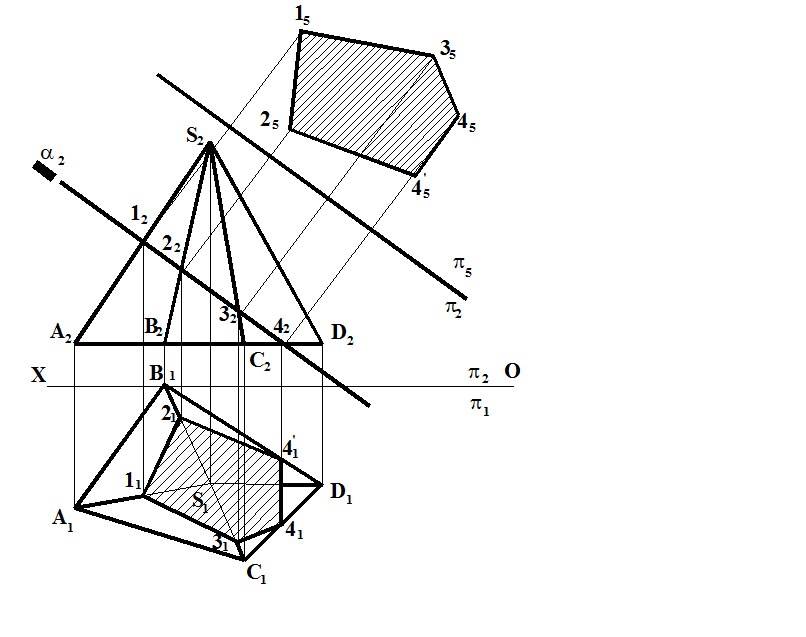 Рис.7.3
Рис.7.3



 Задача 2. Построить отсеченную часть геометрического тела натуральную величину сечения (рис.7.8).
Задача 2. Построить отсеченную часть геометрического тела натуральную величину сечения (рис.7.8).