Статически определимые фермы. Методы вырезания узлов и сквозного сечения

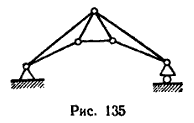
Плоская или пространственная неизменяемая конструкция, составленная из шарнирно соединенных между собой стержней, называется фермой.

На рис. 135 изображена простая плоская ферма (пример пространственной фермы приведен в § 19).

Если число узлов (шарниров) фермы n, а число стержней k то в простой плоской ферме соблюдается условие
k = 2n + 3.

Ферма называется статически определимой, если усилия во всех стержнях фермы, нагруженной в шарнирах, можно определить при помощи уравнений равновесия.

Все плоские простые фермы статически определимы.

Для определения усилий в стержнях ферм употребляются графические или аналитические методы. Рассмотрим только аналитические методы: метод вырезания узлов (задача 103) и метод сквозного сечения – метод Риттера (задача 104).

При использовании метода вырезания узлов необходимо придерживаться следующего порядка:

1) выяснить, какие нагрузки действуют на ферму, как они направлены и где приложены, а затем определить реакции связей, используя уравнения равновесия. Правильность этой части решения нужно обязательно проверить: для проверки можно использовать любое дополнительно составленное уравнение равновесия;

2) затем следует определить усилия в стержнях фермы, начиная с того узла, на который действуют не более двух неизвестных сил, так как в каждом случае на узел действует система сходящихся сил и, следовательно, для одного узла можно составить лишь два уравнения равновесия;

3) вырезав узел, необходимо заменить действие на узел отброшенной части фермы усилиями, действующими вдоль стержней, считая при этом, что все стержни растянуты, а затем составить уравнения равновесия;

4) путем перехода от узла к узлу определяют усилия во всех стержнях, один из узлов при этом остается нерассмотренным; составив уравнения равновесия для этого узла, можно проверить правильность решения задачи.

При определении усилий в стержнях ферм по методу сквозного сечения необходимо придерживаться следующего порядка:

1) прежде всего, так же как и при методе вырезания узлов, выявив все нагрузки, определить реакции опор;

2) мысленно разрезать фермы на две части таким образом, чтобы разрез проходил не более чем через три стержня, усилия в которых неизвестны*, и, отбросив одну из частей, заменить действие отброшенной части на оставшуюся усилиями, направленными вдоль стержней, предполагая при этом, что все разрезанные стержни (с неизвестными усилиями) растянуты;

3) составить три уравнения равновесия; при выборе направлений осей проекций, а также центра моментов нужно исходить из того, чтобы в каждое из уравнений по возможности входило не более одной неизвестной силы.

* При разрезании фермы через четыре и большее число стержней образуется плоская система сил с четырьмя или соответственно большим числом неизвестных. Так как для произвольной плоской системы сил можно составить только три уравнения равновесия, задачу решить нельзя.

Задача 103. Определить усилия в стержнях фермы, нагруженной, как показано на рис. 136, а, тремя силами: Р₁=10 кн; Р₂=20 кн...

Задача 104. Определить усилия в стержнях 4, 5 и 6 фермы, нагруженной тремя силами: Р₁=10, Р₂=20 и Р₃=30 кн, как показано...

 

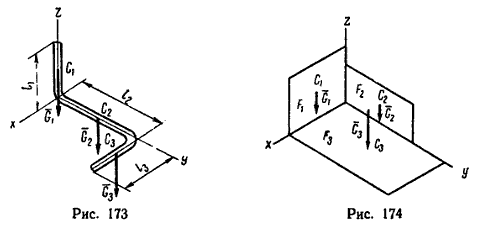
Теоретическая механика:
Центр тяжести

Смотрите также решения задач по нахождению центра тяжести в онлайн решебникахЯблонского (С.8) и Мещерского (§ 9).

Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил (Е. М. Никитин, § 42). Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
x_c = (∑ G_ix_i) / ∑ G_i;
(1)y_c = (∑ G_iy_i) / ∑ G_i;
z_c = (∑ G_iz_i) / ∑ G_i.

Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес G_i каждого отрезка l_i можно представить в виде произведения
G_i = l_id,
где d – постоянный для всей фигуры вес единицы длины материала.

После подстановки в формулы (1) вместо G_i их значений l_id постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий, примут вид:
x_c = (∑ l_ix_i) / ∑ l_i;
(2)y_c = (∑ l_iy_i) / ∑ l_i;
z_c = (∑ l_iz_i) / ∑ l_i.

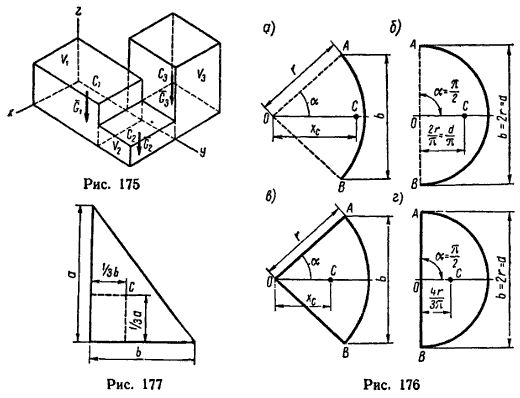
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174), то вес каждой плоскости (поверхности) можно представить так:
G_i = F_ip,
где F_i – площади каждой поверхности, а p – вес единицы площади фигуры.

После подстановки этого значения G_i в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей:
x_c = (∑ F_ix_i) / ∑ F_i;
(3)y_c = (∑ F_iy_i) / ∑ F_i;
z_c = (∑ F_iz_i) / ∑ F_i.

Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
G_i = V_iγ,
где V_i – объем каждой части, а γ – вес единицы объема тела.

После подстановки значений G_i в формулы (1) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов:
x_c = (∑ V_ix_i) / ∑ V_i;
(4)y_c = (∑ V_iy_i) / ∑ V_i;
z_c = (∑ V_iz_i) / ∑ V_i.

При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.

Если известен радиус дуги r и центральный угол 2α, стягиваемый дугой и выраженный в радианах, то положение центра тяжести C (рис. 176, а) относительно центра дуги O определится формулой:
(5)x_c = (r sin α)/α.

Если же задана хорда AB=b дуги, то в формуле (5) можно произвести замену
sin α = b/(2r)
и тогда
(5а)x_c = b/(2α).

В частном случае для полуокружности обе формулы примут вид (рис. 176, б):
(5б)x_c = OC = 2r/π = d/π.

Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы:
(6)x_c = (2r sin α)/(3α).

Если же задана хорда сектора, то:
(6а)x_c = b/(3α).

В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
(6б)x_c = OC = 4r/(3π) = 2d/(3π).

Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.

У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).

При решении задач на определение положения центра тяжести любого однородного тела, составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:

1) выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;

2) разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;

3) определить или длины, или площади, или объемы составных частей;

4) выбрать расположение осей координат;

5) определить координаты центров тяжести составных частей;

6) найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;

7) по найденным координатам указать на рисунке положение центра тяжести тела.