
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение пар в пространстве и на плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема. Действующую на абсолютно твёрдое тело пространственную систему пар можно заменить одной парой, момент которой равен геометрической сумме моментов действующих пар. Пары
Частный случай сложения пар на плоскости. Если на тело действует плоская система пар
Условия равновесия пространственной и плоской Систем пар
Для равновесия пространственной системы пар необходимо и достаточно, чтобы момент результирующей пары (2.8) равнялся нулю
Аналитические условия равновесия пространственной системы пар получим, спроектировав векторное равенство (2.10) на три координатные оси:
Для равновесия пространственной системы пар необходимо и достаточно, чтобы суммы их проекций на три координатные оси равнялись нулю. С учётом того, что пары на плоскости суммируются алгебраически, аналитическое условие равновесия плоской системы пар получим, приравняв равенство (2.9) к нулю:
Для равновесия плоской системы пар необходимо и достаточно, чтобы их алгебраическая сумма равнялась нулю.
Лемма Пуансо о параллельном переносе силы
Действие силы на абсолютно твёрдое тело не изменится, если её перенести параллельно самой себе из данной точки приложения А (рис. 39) в любую другую точку О, приложив при этом пару Пара
Теорема о приведении пространственной произвольной Системы сил к одному центру (основная теорема статики)
Главный вектор
Модуль
Зная проекции главного вектора, находим его модуль:
и направляющие косинусы:
Аналогично определяются проекции главного момента
Тогда модуль главного момента равен
Направляющие косинусы вектора
Частные случаи приведения пространственной произвольной системы сил к одному центру О: 1. 2. 3. 4. 5.
Динамой (силовым винтом) называется совокупность силы и пары, причем сила динамы Или иначе: динамой называется совокупность параллельных векторов силы Если угол
Частный случай приведения плоской системы сил К одному центру
При приведении плоской произвольной системы сил к произвольному центру О получаем одну силу
и одну пару
Модуль
Тогда
Частные случаи приведения плоской системы сил к одному центру: 1. 2. 3. 4. Можно сделать вывод, что плоская произвольная система сил всегда приводится к равнодействующей, если не находится в равновесии (случай 1) и не приводится к одной паре (случай 3).
|
||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 885; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.57 (0.007 с.) |

 и
и 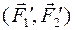 , лежащие в пересекающихся плоскостях I и II и имеющие моменты
, лежащие в пересекающихся плоскостях I и II и имеющие моменты 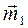 и
и  (рис. 36), согласно этой теореме можно заменить одной парой
(рис. 36), согласно этой теореме можно заменить одной парой  , момент которой равен
, момент которой равен . (2.8)
. (2.8) Момент
Момент 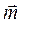 определяется диагональю параллелограмма, построенного на векторах
определяется диагональю параллелограмма, построенного на векторах  , то их векторы
, то их векторы  параллельны (рис. 37). Модуль результирующего вектора системы параллельных векторов равен алгебраической сумме их модулей:
параллельны (рис. 37). Модуль результирующего вектора системы параллельных векторов равен алгебраической сумме их модулей: . (2.9)
. (2.9) Отсюда следует, что плоскую систему пар можно заменить одной парой, момент которой равен алгебраической сумме моментов пар системы.
Отсюда следует, что плоскую систему пар можно заменить одной парой, момент которой равен алгебраической сумме моментов пар системы. . (2.10)
. (2.10)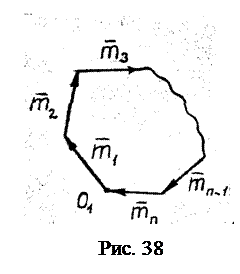 Геометрические условия равновесия (2.10) выражаются в замкнутости многоугольника пар самого на себя (рис. 38): конец последнего вектора
Геометрические условия равновесия (2.10) выражаются в замкнутости многоугольника пар самого на себя (рис. 38): конец последнего вектора  приходит в начало первого.
приходит в начало первого. . (2.11)
. (2.11)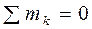 . (2.12)
. (2.12) , равную моменту силы относительно новой точки приложения O
, равную моменту силы относительно новой точки приложения O 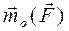 .
. .
.
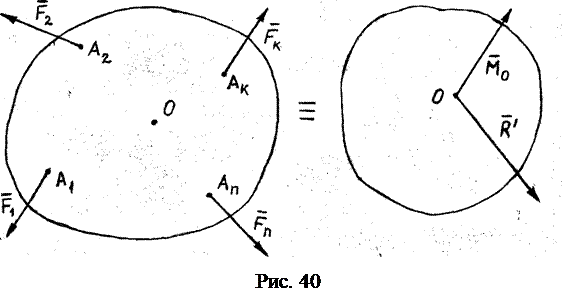 Пространственную произвольную систему сил можно привести к произвольному центру О (рис. 40), приложив в этом центре одну силу
Пространственную произвольную систему сил можно привести к произвольному центру О (рис. 40), приложив в этом центре одну силу 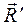 , равную геометрической сумме всех сил и называемую главным вектором данной системы сил, и одну пару
, равную геометрической сумме всех сил и называемую главным вектором данной системы сил, и одну пару  , равную геометрической сумме моментов сил системы относительно центра приведения О и называемую главным моментом системы сил относительно центра приведения О.
, равную геометрической сумме моментов сил системы относительно центра приведения О и называемую главным моментом системы сил относительно центра приведения О. (рис. 40) равны
(рис. 40) равны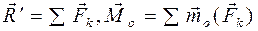 . (2.13)
. (2.13) главного вектора
главного вектора  . (2.14)
. (2.14) (2.15)
(2.15)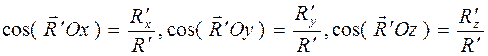 .
. .(2.16)
.(2.16) . (2.17)
. (2.17)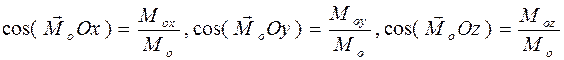 .
. – случай равновесия системы сил.
– случай равновесия системы сил. – система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О.
– система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О. – система приводится к одной паре, момент которой не зависит от выбора центра приведения.
– система приводится к одной паре, момент которой не зависит от выбора центра приведения. и угол между ними
и угол между ними  – система приводится к равнодействующей.
– система приводится к равнодействующей. – система приводится к динаме.
– система приводится к динаме. перпендикулярна плоскости действия пары (рис. 41a).
перпендикулярна плоскости действия пары (рис. 41a). (рис. 41б).
(рис. 41б).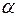 между
между  , то силовой винт называется левым (рис. 41г,д).
, то силовой винт называется левым (рис. 41г,д). .
. Скалярный инвариант, равный скалярному произведению векторов
Скалярный инвариант, равный скалярному произведению векторов  , равен 0:
, равен 0: .
. , (2.18)
, (2.18) , называемую главным моментом системы сил относительно центра приведения О. Учитывая, что при параллельном переносе сил моменты присоединяемых согласно лемме Пуансо пар для плоской системы сил находятся в плоскости действия сил системы, а пары на плоскости суммируются алгебраически, получаем, что для плоской системы сил главный момент относительно центра О равен алгебраической сумме моментов сил системы относительно центра О:
, называемую главным моментом системы сил относительно центра приведения О. Учитывая, что при параллельном переносе сил моменты присоединяемых согласно лемме Пуансо пар для плоской системы сил находятся в плоскости действия сил системы, а пары на плоскости суммируются алгебраически, получаем, что для плоской системы сил главный момент относительно центра О равен алгебраической сумме моментов сил системы относительно центра О: (2.19)
(2.19)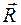 главного вектора
главного вектора  . (2.20)
. (2.20)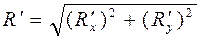 ,
, .
. – система сил находится в равновесии.
– система сил находится в равновесии. – система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О.
– система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О. – система приводится к паре сил, момент которой не зависит от выбора центра приведения О.
– система приводится к паре сил, момент которой не зависит от выбора центра приведения О. . Учитывая, что для плоской системы сил вектор главного момента
. Учитывая, что для плоской системы сил вектор главного момента  , этот случай приведения плоской системы сил аналогичен случаю 4 приведения пространственной системы сил (
, этот случай приведения плоской системы сил аналогичен случаю 4 приведения пространственной системы сил (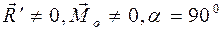 ), значит, в этом случае плоская система сил приводится к равнодействующей.
), значит, в этом случае плоская система сил приводится к равнодействующей.


