
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И специальности 270102 «Промышленное и гражданское строительство»Содержание книги
Поиск на нашем сайте
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА КИНЕМАТИКА
Основы теории и контрольные работы для студентов по направлению подготовки 110300 «Агроинженерия» И специальности 270102 «Промышленное и гражданское строительство» Очной и заочной форм обучения
Кострома 2009 УДК ББК Т
Составители: д.т.н., профессор кафедры деталей машин ФГОУ ВПО Костромская ГСХА С.Н. Разин и ассистент А.Е. Березкина
Рецензенты: доцент кафедры «Сопротивление материалов и графика» ФГОУ ВПО Костромская ГСХА Яцюк И.А. и доцент кафедры «Сельскохозяйственные машины», к.т.н. Волхонов М.С.
Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства ФГОУ ВПО Костромская ГСХА, протокол № от 2006 г. Т Теоретическая механика. Кинематика: основы теории и контрольные работы для студентов по направлению подготовки 110300 «Агроинженерия» и специальности 270102 «Промышленное и гражданское строительство» очной и заочной форм обучения / сост. С.Н. Разин и А.Е. Березкина. – Кострома: Изд-во КГСХА, 2006. – 35 с. Пособие содержит изложение теоретического материала в виде кратких ответов на вопросы по кинематике, выносимые на экзамен, и примеры решения типовых задач. После изложения теоретического материала приведены 4 задания по основным разделам кинематики: кинематика точки, поступательное и вращательное движения твердого тела, плоскопараллельное движение твердого тела, сложное движение точки. В качестве прототипа выбраны методические указания и контрольные задания по “Теоретической механике”, под редакцией С.М. Тарга, издательство «Высшая школа», 1982. Пособие предназначено для самостоятельной работы студентов по направлению подготовки 110300 «Агроинженерия» и специальности 270102 «Промышленное и гражданское строительство» очной и заочной форм обучения. УДК ББК Костромская государственная Сельскохозяйственная академия, 2009 Оглавление
Указания Решение каждой из задач необходимо начинать на развороте тетради (на четной странице, начиная со второй). Сверху указывается номер задачи, выполняется чертеж в соответствующем масштабе и записывается условие задачи. Текст задачи не переписывается. Чертеж должен быть аккуратным и наглядным, с нанесением всех размеров и обозначений. Решение задачи необходимо сопровождать краткими пояснениями. На каждой странице следует оставлять поля для замечаний рецензента. Работы, не отвечающие перечисленным требованиям, проверяться не будут, и будут возвращены для переделки Естественные оси координат. Естественные оси двигаются вместе с точкой и изменяют свое положение в пространстве. Этих осей три (рис.6): касательная, главная нормаль, Единичный вектор касательной - Соприкасающаяся плоскость - предельное положение плоскости, проходящей через т. М1, лежащую на кривой и касательную в т. М, при стремлении т. М1 к т. М. Единичный вектор главной нормали
5. Скорость при векторном способе задания движения. Пусть за время Δt точка переместилась из М в М
Δt Из рис. 7 видно, что:
Δt то есть, скорость точки в данный момент времени равна первой производной от радиуса вектора по времени. Из рисунка видно, что вектор скорости в данный момент времени занимает положение касательной. Скорость измеряется в м/с. 6. Ускорение при векторном способе задания движения. Средним ускорением называется отношение вектора изменения скорости к промежутку времени, за которое оно произошло:
Δt Ускорение равно первой производной от скорости или второй производной от радиуса вектора по времени:
Ускорение 7. Скорость при координатном способе задания движения. Известно, что:
С другой стороны: сравнивая (1) и (2) получим: vх = dx/dt; vу = dy/dt; v
соs( 8. Ускорение при координатном способе задания движения. Известно, что:
с другой стороны: сравнивая (1) и (2) получим: а x =dv x /dt =d Модуль ускорения: | соs ( Формула Эйлера.
vM = lim Δs / Δt = lim (R ∙ Δφ)/ Δt = R∙ω. Δt
Ускорение касательное: a τ = d vM /dt = d(R ∙ ω)/dt = R ∙ dω/dt = R ∙ ε. an = vM тогда полное ускорение: аМ = Угол наклона полного ускорения к радиусу не зависит от R: tgα = aτ / an = ε / ω2. Скорость т.М можно найти и с помощью векторного произведения:
Можно проверить, что первое слагаемое есть - a τ, а второе - an. Задача К1 По заданным уравнениям движения точки в плоскости xy:
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки. В данной задаче все искомые величины нужно определить только для момента времени t1 = π/6 c. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует применить известные из тригонометрии формулы:
При выборе масштабов построения траектории, скоростей и ускорений следует учитывать, что они должны быть стандартными, то есть из ряда: 1, 2, 25, 4, 5. При этом изображаемые вектора должны быть достаточно крупными (50 - 100 мм). Таблица К1
Пример К1. Даны уравнения движения точки в плоскости xy:
Определить уравнение траектории точки; для момента времени t1=1c найти скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории. Решение. 1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу.
следовательно: Отсюда окончательно находим следующее уравнение траектории точки (рис. К1): 2. Скорость точки найдем по ее проекциям на координатные оси:
и при t = 1c: 3. Аналогично найдем ускорение точки:
и при t = 1c: 4. Касательное ускорение найдем, дифференцируя по времени равенство: Подставив полученные ранее значения, найдем, что при t = 1c: aτ = 0,66 см/с2. 5. Нормальное ускорение точки:
6. Радиус кривизны траектории: При построении скоростей следует в данном случае выбрать масштаб: μ v = 0,02 l vx = │vx │ / μ v = 1,11/0,02 ≈ 56 мм, l vy = │vy │ / μ v = 0,73/0,02 ≈ 37 мм; или μ v = 0,01 l vx = │vx │ / μ v = 1,11/0,01 = 111 мм, l vy = │vy │ / μ v = 0,73/0,01 = 73 мм. При построении ускорений следует выбрать масштаб: μ a = 0,01 l ax = │ a x │ / μ a = 0,87/0,01 = 87 мм, l ay = │ a y │ / μ a = 0,12/0,01 = 12 мм; l aτ = │ aτ │ / μ a = 0,66/0,01 = 66 мм, l an = │ an │ / μ a = 0,58/0,01 = 58 мм. Найденные длины отрезков откладываем из точки с координатами: при t = 1c: Замечание: при построении следует учесть, что l ay необходимо отложить вниз, так как: ay < 0, а aτ – по направлению скорости, так как aτ > 0. Задача К2 Механизм состоит из ступенчатых колес 2-3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 1, привязанного к концу нити, намотанной на одно из колес (рис. К2.0-К2.9, табл. К2). Радиусы ступеней равны соответственно: у колеса 2 – r2=6 см, R2=8 см, у колеса 3 – r3=12 см, R3 = 16 см. На ободьях колес расположены точки А и В. В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где: Определить в момент времени t 1 = 2 c указанные в таблице в столбцах «Найти» скорости (υ – линейные, ω – угловые) и ускорения (а – линейные, ε – угловые) соответствующих точек или тел (υ1 – скорость груза 1 и т.д.). Указания. Задача К2 – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны ременной передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы; при этом считается, что ремень по ободу колеса не скользит. Таблица К2
Пример К2. Рейка 1, ступенчатое колеса 2 с радиусами R2 и r2 и колесо 3 радиуса R3, скрепленное с валом радиуса r3, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К2). Рейка движется по закону s1=f(t). Дано: R2=6 см, r2=4 см, R3=8 см, r3=3 см, s1=3t3 (s- в сантиметрах, t – в секундах), А – точка обода колеса 3, t1 = 3 c. Определить: ω3, υ4, ε3, αA в момент времени t = t1.
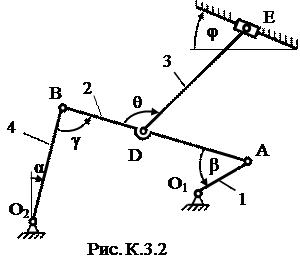
1. Определим сначала угловые скорости всех колес как функции времени t. Зная закон движения рейки 1, находим ее скорость Так как рейка и колесо 2 находятся в зацеплении, то υ2= υ1 или ω2R2= υ1. Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, u2= υ3 или ω2r2= ω3R3. Из этих равенств находим: Тогда для момента времени t1 = 3 c получим: ω3 =6,75c-1. 2. Определим υ4. Так как υ4 = υB = ω3r3, то при t1=3 c: υ4 =20,25 см/с. 3. Определяем ε3. Учитывая, что ε3= ε3=4,5 с-2. 4. Определяем aA. Для точки А: Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис. К2. Задача К3 Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е (рис. К3.0 – К3.7) или из стержней 1, 2, 3 и ползунов В и Е (рис. К3.8, К3.9), соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами; точка D находится в середине стержня АВ. Длина стержней: l 1 = 0,4 м, l 2 = 1,2 м, l 3 = 1,4 м, l 4 = 0,6 м. Положение механизма определяется углами α, β, γ, φ, θ. Значения этих углов и других заданных величин указаны в табл. К3а (для рис. 0-4) или в табл. К3б (для рис. 5-9); при этом в табл. К3а ω1 и ω4 – величины постоянные. Определить величины, указанные в таблицах в столбцах «Найти». Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол γ на рис. 8 следует отложить от DB по ходу часовой стрелки, а на рис. 9 – против хода часовой стрелки и т.д.). Построение чертежа начинать со стержня, направление которого определяется углом α; ползун с направляющими для большей наглядности изобразить так, как в примере К3 (см. рис. К3, б). Заданные угловую скорость и угловое ускорение считать направленными против хода часовой стрелки, а заданные скорость Указания. Задача К3 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности. При определении ускорений точек механизма исходить из векторного равенства Таблица К3а (к рис. К3.0 – К3.4)
Таблица К3б (к рис. К3.5 – К3.9)
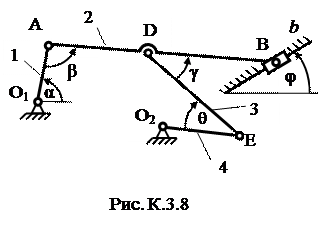
Пример К3. Механизм (рис. К3, а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами. Дано: a=60º, b=150º, g=90º, j=30º, q=30º, AD = DB, l 1 = 0,4 м, l 2 = 1,2 м, l 3 = 1,4 м, w1 = 2 с-1, e1 = 7 с-2 (направление w1 и e1 – против хода часовой стрелки). Определить: uB, uE, w2, aB, e3. Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. К3, б). 2. Определяем uВ. Точка В принадлежит стержню АВ. Чтобы найти uВ, надо знать скорость какой-нибудь другой точки этого стержня и направление
Направление
3. Определяем
Чтобы вычислить С3D и C3B, заметим, что
Так как точка Е принадлежит одновременно стержню О2Е, вращающемуся вокруг О2, то
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.75.242 (0.012 с.) |

 бинормаль.
бинормаль. (тау) направлен по касательной к траектории в сторону положительного отсчета дуги.
(тау) направлен по касательной к траектории в сторону положительного отсчета дуги. - перпендикулярен
- перпендикулярен  - перпендикулярен соприкасающейся плоскости и направлен в ту сторону, откуда вращение от
- перпендикулярен соприкасающейся плоскости и направлен в ту сторону, откуда вращение от  к
к  ) называется спрямляющей.
) называется спрямляющей. (рис.7), вектор Δ
(рис.7), вектор Δ  - вектор перемещения. Средней скоростью точки за время Δt называется вектор
- вектор перемещения. Средней скоростью точки за время Δt называется вектор  ср = Δ
ср = Δ 
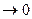
 ср=Δ
ср=Δ 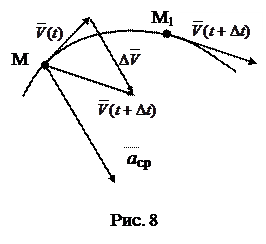 Ускорением точки в данный момент называется предел этого отношения при стремлении промежутка времени к нулю.
Ускорением точки в данный момент называется предел этого отношения при стремлении промежутка времени к нулю.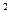 .
. +y·
+y·  +z·
+z·  , тогда (т.к.
, тогда (т.к. 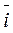 ,
,  ,
,  - const):
- const): +dy/dt·
+dy/dt·  +dz/dt·
+dz/dt·  , (1)
, (1) ·
·  +v
+v  ·
·  ·
·  . (2)
. (2) =
=  , а так же направляющие косинусы:
, а так же направляющие косинусы: ) = vx / |
) = vx / |  + vy·
+ vy·  + vz·
+ vz·  , тогда:
, тогда: +dvz /dz ·
+dvz /dz ·  , (1)
, (1) + ау ·
+ ау · 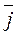 + аz·
+ аz·  , направляющие косинусы:
, направляющие косинусы: ) = аy / |
) = аy / |  ) = аz / |
) = аz / |  Пусть за время Δt тело повернулось на угол Δφ, тогда т. М опишет дугу окружности длиной Δs (рис.11а). Найдем скорость т.М:
Пусть за время Δt тело повернулось на угол Δφ, тогда т. М опишет дугу окружности длиной Δs (рис.11а). Найдем скорость т.М: = R
= R  .
. , это и есть формула Эйлера. Здесь
, это и есть формула Эйлера. Здесь  - радиус вектор точки М (рис 11б). Взяв производную от этой формулы, получим:
- радиус вектор точки М (рис 11б). Взяв производную от этой формулы, получим: =d
=d  /dt=d
/dt=d  /dt×
/dt× 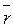 +
+  ×
×  +
+  (табл. К1) требуется найти уравнение траектории и для момента времени t1 = π/6 c определить скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории. Построить на рисунке все найденные скорости и ускорения в соответствующих масштабах.
(табл. К1) требуется найти уравнение траектории и для момента времени t1 = π/6 c определить скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории. Построить на рисунке все найденные скорости и ускорения в соответствующих масштабах.


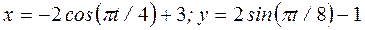 , (x, y – в сантиметрах, t - в секундах).
, (x, y – в сантиметрах, t - в секундах). или
или 
 Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим:
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим:
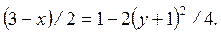


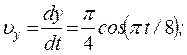




 .
. ax = 0,87 см/с2, ay = - 0,12 см/с2, a = 0,88 см/с2.
ax = 0,87 см/с2, ay = - 0,12 см/с2, a = 0,88 см/с2. . Получим:
. Получим: 
 Подставляя сюда найденные числовые значения a1 и a1τ, получим, что при t = 1 c: an = 0,58 см/с2.
Подставляя сюда найденные числовые значения a1 и a1τ, получим, что при t = 1 c: an = 0,58 см/с2. Подставляя сюда числовые значения υ 1 и a 1 n, найдем, что при t = 1 c: ρ = 3,05 см.
Подставляя сюда числовые значения υ 1 и a 1 n, найдем, что при t = 1 c: ρ = 3,05 см. , тогда:
, тогда:
 - закон вращения колеса 2, s4(t) – закон движения рейки 4, ω2(t) – закон изменения угловой скорости колеса 2, υ1(t) – закон изменения скорости груза 1 и т.д. (везде φ - выражено в радианах, s - в сантиметрах, t – в секундах). Положительное направление для φ и ω против хода часовой стрелки, для s1, s4 и υ1, υ4 – вниз.
- закон вращения колеса 2, s4(t) – закон движения рейки 4, ω2(t) – закон изменения угловой скорости колеса 2, υ1(t) – закон изменения скорости груза 1 и т.д. (везде φ - выражено в радианах, s - в сантиметрах, t – в секундах). Положительное направление для φ и ω против хода часовой стрелки, для s1, s4 и υ1, υ4 – вниз.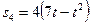
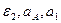









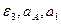




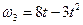
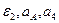
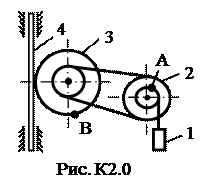
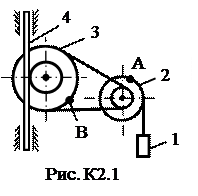





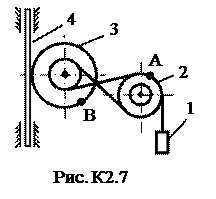


 Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса Ri), через υi, а точек, лежащих на внутренних ободах (радиуса ri), - через ui.
Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса Ri), через υi, а точек, лежащих на внутренних ободах (радиуса ri), - через ui. (1)
(1)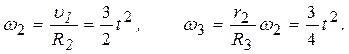
 = 1,5 t. Тогда при t 1=3 с получим:
= 1,5 t. Тогда при t 1=3 с получим: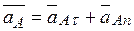 , где численно
, где численно  Тогда, для момента времени t1=3 с, имеем:
Тогда, для момента времени t1=3 с, имеем: 
 и ускорение
и ускорение  - от точки В к b (на рис. 5-9).
- от точки В к b (на рис. 5-9). , где А – точка, ускорение
, где А – точка, ускорение  которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то
которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то  ; В – точка, ускорение
; В – точка, ускорение 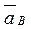 которой нужно определить (если точка В движется по дуге окружности радиуса l, то
которой нужно определить (если точка В движется по дуге окружности радиуса l, то  , где численно
, где численно  ; входящая сюда скорость υB определяется так же, как и скорости других точек механизма).
; входящая сюда скорость υB определяется так же, как и скорости других точек механизма).







 . По данным задачи, учитывая направление w1, можем определить
. По данным задачи, учитывая направление w1, можем определить  ; численно
; численно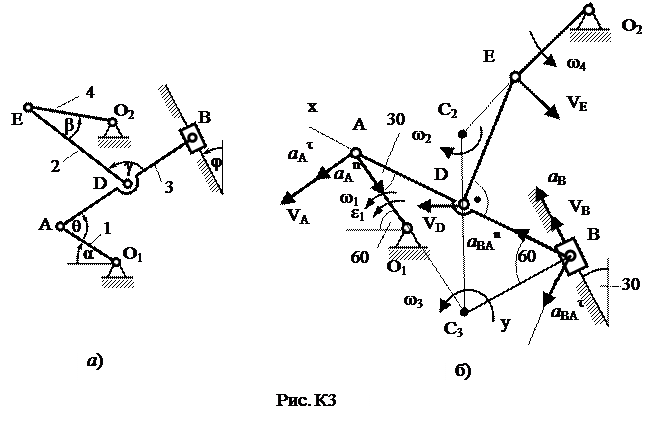
 (1)
(1) найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь зная
найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь зная  и направление
и направление  , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 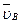 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим (2)
(2) . Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить
. Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить 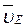 , надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная
, надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная  и
и  перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора 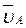 определяем направление поворота стержня АВ вокруг МЦС С3. Вектор
определяем направление поворота стержня АВ вокруг МЦС С3. Вектор  перпендикулярен отрезку С3D, соединяющему точки D и C3, и направлен в сторону поворота. Величину uD найдем из пропорции
перпендикулярен отрезку С3D, соединяющему точки D и C3, и направлен в сторону поворота. Величину uD найдем из пропорции (3)
(3)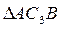 прямоугольный, так как острые углы в нем равны 30 и 60º, и что C3B=АВsin30º=0,5AB=BD. Тогда
прямоугольный, так как острые углы в нем равны 30 и 60º, и что C3B=АВsin30º=0,5AB=BD. Тогда 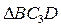 является равносторонним и C3B= С3D. В результате равенство (3) дает
является равносторонним и C3B= С3D. В результате равенство (3) дает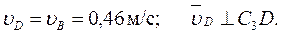 (4)
(4)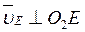 . Тогда, восставляя из точек Е и D перпендикуляры к скоростям
. Тогда, восставляя из точек Е и D перпендикуляры к скоростям 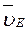 и
и 


