
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При выполнении контрольных работ следует Номер рисунка выбирать по последней цифре шифра, а условие задачи в соответствующей таблице по предпоследней цифре шифра.Содержание книги
Поиск на нашем сайте
Пример: если шифр 892341, то при решении задачи К1 следует взять рисунок К1.1, а условие №4. Литература
1. Векторный способ задания движения точки. Задать движение, это значит - уметь определить положение точки в каждый момент времени. Векторный способ задания движения заключается в задании вектор функции: Линия, которую описывает точка при своем движении, называется траекторией. 2. Координатный способ задания движения точки.
3. Естественный способ задания движения точки.
1) траектории точки: у = f(х), 2) начала отсчета (точка О), 3) положительного направления отсчета, 4) закона движения s = s(t), где s - дуговая координата. Естественные оси координат. Естественные оси двигаются вместе с точкой и изменяют свое положение в пространстве. Этих осей три (рис.6): касательная, главная нормаль, Единичный вектор касательной - Соприкасающаяся плоскость - предельное положение плоскости, проходящей через т. М1, лежащую на кривой и касательную в
т. М, при стремлении т. М1 к т. М. Единичный вектор главной нормали 5. Скорость при векторном способе задания движения. Пусть за время Δt точка переместилась из М в М
Δt Из рис. 7 видно, что:
Δt то есть, скорость точки в данный момент времени равна первой производной от радиуса вектора по времени. Из рисунка видно, что вектор скорости в данный момент времени занимает положение касательной. Скорость измеряется в м/с. 6. Ускорение при векторном способе задания движения. Средним ускорением называется отношение вектора изменения скорости к промежутку времени, за которое оно произошло:
Δt Ускорение равно первой производной от скорости или второй производной от радиуса вектора по времени:
Ускорение 7. Скорость при координатном способе задания движения. Известно, что:
С другой стороны: сравнивая (1) и (2) получим: vх = dx/dt; vу = dy/dt; v
соs( 8. Ускорение при координатном способе задания движения. Известно, что:
с другой стороны: сравнивая (1) и (2) получим: а x =dv x /dt =d Модуль ускорения: | соs (
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.27.88 (0.008 с.) |

 =
=  , t
, t  ,..., получим вектора
,..., получим вектора  =
=  =
=  При этом способе задается 3 функции (при движении в пространстве), определяющие три координаты точки в каждый момент времени. Системы координат могут быть разными, например: прямоугольная декартова, цилиндрическая или сферическая система координат. В первом случае задается: х=х(t); y=у(t); z=z(t) - это и есть уравнения движения точки (рис.2). в цилиндрической системе координат (рис.3) задаются: ρ= ρ(t); φ= φ (t); z=z(t). В сферической (рис.4): φ = φ(t); θ= θ(t); r=r(t). если движение задано в какой - то из этих систем координат, то всегда можно перейти к заданию движения в любой из двух других.
При этом способе задается 3 функции (при движении в пространстве), определяющие три координаты точки в каждый момент времени. Системы координат могут быть разными, например: прямоугольная декартова, цилиндрическая или сферическая система координат. В первом случае задается: х=х(t); y=у(t); z=z(t) - это и есть уравнения движения точки (рис.2). в цилиндрической системе координат (рис.3) задаются: ρ= ρ(t); φ= φ (t); z=z(t). В сферической (рис.4): φ = φ(t); θ= θ(t); r=r(t). если движение задано в какой - то из этих систем координат, то всегда можно перейти к заданию движения в любой из двух других. Он заключается в задании (рис.5):
Он заключается в задании (рис.5): бинормаль.
бинормаль. (тау) направлен по касательной к траектории в сторону положительного отсчета дуги.
(тау) направлен по касательной к траектории в сторону положительного отсчета дуги.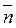 - перпендикулярен
- перпендикулярен  - перпендикулярен соприкасающейся плоскости и направлен в ту сторону, откуда вращение от
- перпендикулярен соприкасающейся плоскости и направлен в ту сторону, откуда вращение от  к
к  ) называется спрямляющей.
) называется спрямляющей. - вектор перемещения. Средней скоростью точки за время Δt называется вектор
- вектор перемещения. Средней скоростью точки за время Δt называется вектор  ср = Δ
ср = Δ 
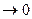
 ср=Δ
ср=Δ 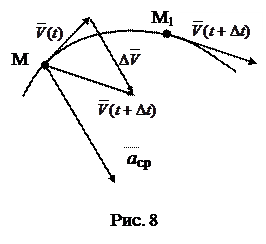 Ускорением точки в данный момент называется предел этого отношения при стремлении промежутка времени к нулю.
Ускорением точки в данный момент называется предел этого отношения при стремлении промежутка времени к нулю.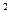 .
. +y·
+y·  +z·
+z·  , тогда (т.к.
, тогда (т.к. 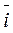 ,
,  ,
,  - const):
- const): +dy/dt·
+dy/dt·  +dz/dt·
+dz/dt·  , (1)
, (1) ·
·  +v
+v  ·
·  ·
·  . (2)
. (2) =
=  , а так же направляющие косинусы:
, а так же направляющие косинусы: ) = vx / |
) = vx / |  + vy·
+ vy·  + vz·
+ vz·  , тогда:
, тогда: +dvz /dz ·
+dvz /dz ·  , (1)
, (1) + ау ·
+ ау · 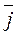 + аz·
+ аz·  , направляющие косинусы:
, направляющие косинусы: ) = аy / |
) = аy / |  ) = аz / |
) = аz / | 


