
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные формы констант равновесия и связь между ними.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кроме того константу равновесия можно выразить через парциальные давления реагирующих веществ:
Константу равновесия можно выразить через числа молей веществ - участников реакции:
Константу равновесия можно выразить и через мольные доли участников реакции:
В общем случае kC
Откуда
где Для идеальных газов их парциальные давления связаны с общим давлением соотношением:
поэтому:
или
Далее:
или окончательно:
Уравнение изотермы химической реакции. Химическое сродство. Для реакции (4.87) ход рассуждений, использованный в параграфе 12 в условиях V, T=const дает:
или сокращенно
где которой умножено на соответствующий коэффициент. Замена концентраций парциальными давлениями дает в условиях P, T = const:
Уравнения (4.92) и (4.93) - уравнения изотермы химической реакции или уравнения Вант-Гоффа. Способность различных веществ взаимодействовать между собой с образованием новых веществ была замечена давно и получила наименование химического сродства. Критерий оценки химического сродства был найден не сразу. Несостоятельным оказалось предположение о равенстве теплового эффекта реакции и сродства. Голландский физико - химик Вант-Гофф предложил новую теорию химического сродства, которая, не объясняя его природу, дает возможность количественно оценить его: в качестве мерила химического сродства предложено использовать полную максимальную работу реакции, если реакция протекает при V = const:
или максимальную полезную работу, если реакция протекает в условиях p = const:
где значения AV и AP могут быть рассчитаны и по уравнениям изотермы химической реакции (4.94). Для того, чтобы иметь возможность сравнивать сродство различных веществ, было введено понятие нормального (стандартного) сродства. К уравнению нормального сродства легко подойти, если начальные парциальные давления или концентрации реагентов равны единице. Тогда:
Сравнивая Замечание. Для растворов правильнее пользоваться не молярными концентрациями (Сi) в случае расчета химического сродства, а мольными долями компонентов.
Направление реакций и условие равновесия. Если начальные парциальные давления или концентрации реагирующих газов совпадают с равновесными, то Чем более далеки парциальные давления или концентрации реагентов от равновесных, тем больше величина работы, выше сродство, как это следует из уравнения изотермы химической реакции. Согласно этому же уравнению реакция идет в направлении, указанном ее уравнением, если Реакция пойдет в обратном направлении, если Чем больше АР(V), тем больше kP(C) и тем дальше пойдет реакция при заданных начальных парциальных давлениях (или концентрациях), так как большим kP(C) отвечают большие значения равновесных концентраций конечных продуктов реакции (числитель) и малые равновесные концентрации остающихся исходных продуктов реакции (знаменатель). Поэтому очевидно, что константа равновесия химической реакции однозначно определяет полноту протекания химической реакции.
Зависимость константы равновесия От температуры и давления. Полученные сведения о равновесии можно дополнить, установив зависимость константы равновесия от температуры и давления. Дифференцирование уравнения (4.93) по температуре дает:
Полученное выражение и значение АР из уравнения (4.93) необходимо ввести в уравнение Гиббса - Гельмгольца:
и получить
откуда после упрощений:
По аналогии:
Или, учитывая соотношения
Полученные уравнения вида (4.95) и (4.96) - это уравнения изобары и изохоры химической реакции, устанавливающие зависимость константы равновесия химической реакции от температуры. Интегрирование уравнений (4.95) и (4.96) в обобщенной форме их записи позволяет получить точное решение в виде:
Если предположить, что Q
Из (4.98) видно, что Сделанные выводы представляют собой частный случай принципа Ле-Шателье (или принцип подвижного равновесия), который позволяет в простейших случаях предвидеть направление течения химической реакции. Согласно этому принципу, изменение внешних условий (Т и Р) термодинамической равновесной системы вызывает в ней процессы, противодействующие произвольному изменению. Например для реакций вида: N2 + O2 2NО + O2 повышение температуры сдвинет первое равновесие в сторону образования NO, а второе равновесие - в сторону диссоциации NО2. Константа равновесия kP пропорциональна функции
Но это вовсе не означает, что при изменении давления количество веществ, находящихся в равновесии не изменяется. Поэтому изменение давления влияет на kN реакции. Из уравнения (4.90):
и затем:
Отсюда после дифференцирования при постоянной температуре:
Используя уравнение состояния идеального газа PV = nRT и считая Р и Т постоянными: Р
называемое уравнением Планка. Если химическая реакция сопровождается уменьшением количества вещества (
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.104 (0.007 с.) |

 - константа равновесия, выраженная через молярные концентрации веществ, участвующих в химической реакции.
- константа равновесия, выраженная через молярные концентрации веществ, участвующих в химической реакции. .
. .
. .
. kP
kP 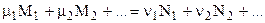 . (4.87)
. (4.87) .
. , (4.88)
, (4.88) - изменение количества вещества в результате химической реакции.
- изменение количества вещества в результате химической реакции. ,
,
 . (4.89)
. (4.89)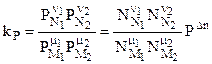
 . (4.90)
. (4.90) (4.91)
(4.91)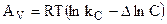 , (4.92)
, (4.92) - алгебраическая сумма логарифмов начальных концентраций, каждое из слагаемых
- алгебраическая сумма логарифмов начальных концентраций, каждое из слагаемых . (4.93)
. (4.93)

 и
и . (4.95)
. (4.95) или
или  различных веществ, получают характеристику удаленности данной системы от состояния равновесия.
различных веществ, получают характеристику удаленности данной системы от состояния равновесия. и AP(V) = 0. Это означает, что в состоянии равновесия реакция не идет и система не работает.
и AP(V) = 0. Это означает, что в состоянии равновесия реакция не идет и система не работает. . При этом AP(V) > 0, т. е. система сама совершает работу.
. При этом AP(V) > 0, т. е. система сама совершает работу. .
. . (4.94)
. (4.94)
 ,
,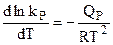 . (4.95)
. (4.95) . (4.96)
. (4.96) и
и  :
: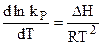 и
и 
 . (4.97)
. (4.97) . (4.98)
. (4.98) , причем, если Q > 0 (экзотермическая реакция), то с ростом температуры значение k уменьшается, а если Q < 0 (эндотермическая реакция), то при увеличении температуры величина k, наоборот, увеличивается.
, причем, если Q > 0 (экзотермическая реакция), то с ростом температуры значение k уменьшается, а если Q < 0 (эндотермическая реакция), то при увеличении температуры величина k, наоборот, увеличивается. 2NO - 180,0 кДж,
2NO - 180,0 кДж, , но стандартная функция энергия Гиббса определяется при строго фиксированном давлении. Следовательно, некорректно обсуждать изменение kP при изменении давления для случая идеальных газов. Таким образом при постоянной температуре:
, но стандартная функция энергия Гиббса определяется при строго фиксированном давлении. Следовательно, некорректно обсуждать изменение kP при изменении давления для случая идеальных газов. Таким образом при постоянной температуре: . (4.99)
. (4.99)
 .
.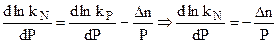 .
. V =
V =  в полученное уравнение kN = f (P), можно получить уравнение:
в полученное уравнение kN = f (P), можно получить уравнение: , (4.100)
, (4.100) , и с увеличением давления в системе равновесие смещается в сторону конечных продуктов химической реакции, что обеспечивает большую полноту превращения исходных продуктов химической реакции в конечные.
, и с увеличением давления в системе равновесие смещается в сторону конечных продуктов химической реакции, что обеспечивает большую полноту превращения исходных продуктов химической реакции в конечные.


