
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
в жидком состоянии и ограниченной в твердом.Содержание книги
Поиск на нашем сайте
Таких систем примерно на порядок больше, чем ранее рассмотренных.
Системы эвтектического типа.
Диаграмма эвтектического типа изображена на рис. 6.5. Линия A’EB’ - линия ликвидус, линия A’аEbB’ - солидус, линия аEb - эвтектическая горизонталь. Эвтектика в переводе с греческого - легкоплавящаяся. Линии ас и bd - линии сольвус или линии предельной растворимости компонентов друг в друге. Области При ТИСХ сплав состава x1 представлен однородной жидкостью, которая по достижении температуры эвтектической горизонтали (ТЕ) насыщается одновременно по отношению к двум твердым растворам:
В результате эвтектического превращения образуется эвтектическая смесь двух фаз: с = k - f + 1 = 2 - 3 + 1 = 0, т. е. нонвариантное равновесие в двухкомпонентной системе реализуется при постоянной температуре (ТЕ) и постоянных составах фаз ( При дальнейшем охлаждении составы равновесных фаз не изменяются. Системы перитектического типа. “Перитектос” - окружение (греч.). Диаграмма состояния перитектического типа изображена на рис. 6.6. До температуры точки 1 охлаждается однородная жидкость, которая при температуре Т1 насыщается относительно
характеризующим процесс первичной кристаллизации.
При температуре ТР (температура перитектической горизонтали Раb) жидкость состава точки Р становится ненасыщенной по отношению к выпавшим кристаллам Уравнение (6.9) описывает процесс перитектической кристаллизации. Число степеней свободы для системы при ТР: с = k - f + 1 = 2 - 3 + 1 = 0. Системы с промежуточными фазами.
Системы с промежуточными фазами делятся на две группы: с конгруентно (рис. 6.7, а) и с инконгруентно плавящимися промежуточными фазами (рис. 6.7, б). Если составы жидкости и твердой фазы при температуре плавления совпадают (т. D), то такие системы называют системами с конгруентно плавящейся промежуточной фазой (рис.6.7, а), а если составы равновесных фаз при температуре плавления не совпадают (рис. 6.7, б), то это системы с инконгруентно плавящейся промежуточной фазой. Точка D называется дистектической (трудноплавящейся) точкой. Системы с ограниченной растворимостью в жидком состоянии. Диаграммы состояния систем с ограниченной растворимостью в жидком состоянии представлены диаграммами двух типов: с монотектическим и синтектическим превращениями (рис. 6.8 а,б). Линия nkm - купол расслоения - линия ограниченной растворимости в жидком состоянии. При охлаждении сплава x1 (рис. 6.8, а) и достижении им температуры точки 1 жидкость состава точки 1 насыщается по отношению к другой жидкости состава точки 1’. В интервале (Т1 - Т2) идет процесс расслоения, сопровождающийся изменением состава жидкостей:
Системы синтектического типа в реальных металлургических системах встречаются редко. Смысл синтектического превращения может быть представлен схемой вида:
для которого с = k - f + 1 = 2 - 3 + 1 = 0.
Трехкомпонентные системы. На практике наряду с двухкомпонентными системами гораздо чаще приходится иметь дело с системами, составленными из трех и более компонентов. Уравнение состояния трехкомпонентных систем связывает между собой пять параметров и имеет следующий вид:
Из (6.12) следует, что диаграмма состояния трехкомпонентной системы не может быть изображена на плоскости. Полагая, что Р = const и С1 + С2 + С3 = 1, если способ выражения состава сплавов мольные доли, трехкомпонентную диаграмму можно построить в трехмерном пространстве. Составы трехкомпонентных сплавов принято изображать на плоскости с помощью концентрационного треугольника. В вершинах треугольника располагаются чистые компоненты А, В и С, а три его стороны отражают составы двойных сплавов. Ось, перпендикулярная плоскости концентрационнго треугольника - температурная ось. Свойства концентрационного треугольника. Первое свойство. Если из какой-то точки М, лежащей в плоскости треугольника опустить три перпендикуляра на стороны, то: МА + МВ + МС = const = BD, где BD - высота концентрационного треугольника (рис. 6.9, а). Если BD принять за 100%, то каждый из перпендикуляров - концентрация каждого из компонентов в сплаве: Ма = % А; Мb = % B; Mc = % C. Второе свойство. Если через точку М, лежащей в плоскости треугольника, провести три параллельные сторонам треугольника прямые, то сумма отрезков Аb, Bc и Са, отсекаемых этими прямыми на сторонах треугольника - величина постоянная и равная стороне треугольника: Аb + Вс + Са = const = АВ. Если АВ = % В, Вс = % С и Са = % А, то состав трехкомпонентного сплава определен.
Таким образом, зная свойства равностороннего треугольника, по положению фигуративной точки можно оценить состав трехкомпонентного сплава или, зная его состав, можно найти положение фигуративной точки в плоскости концентрационного треугольника. Как и для двухкомпонентных систем, сложность диаграмм состояния трехкомпонентных систем зависит от взаимной растворимости компонентов и от возможности образования между ними химических соединений. Наиболее простой является диаграмма состояния трехкомпонентной системы с неограниченной растворимостью компонентов в жидком и твердом состояниях (рис. 6.10). Для диаграммы на рис. 6.10 ТS (B) > ТS (A) > ТS (С) т. А’, B’ и C’ - температуры плавления чистых компонентов.
Грани призмы - двойные системы с неограниченной растворимостью компонентов в твердом и жидком состояниях. Через три ликвидуса проходит поверхность ликвидуса. Выше поверхности ликвидуса находится объем жидких растворов (L). Через три солидуса проходит поверхность солидуса. Ниже поверхности солидуса располагается объем твердых растворов ( Сплав состава т. М (рис. 6.10) при Т > Т1 находится в состоянии ненасыщенного жидкого раствора. Кристаллизация сплава начинается при Т1, лежащей на поверхности ликвидуса. Состав первых кристаллов При дальнейшем понижении температуры от Т1 до Т2 жидкость постепенно принимает состав т. 2’ и исчезает, а кристаллы
Ниже температуры Т2 происходит охлаждение кристаллов твердого раствора При работе с диаграммами состояния трехкомпонентных систем удобно пользоваться их разрезами - поли- и изотермическими. Изотермические разрезы характеризуют фазовые равновесия в тройных сплавах, а по политермическим разрезам устанавливают температуры начала и конца кристаллизации сплавов и т.д. _______ В данной главе рассмотрен ряд более или менее сложных систем, изучение которых с помощью лишь одного термодинамического метода затруднено. С помощью же диаграмм состояния свойства таких систем описывать достаточно просто. Но лишь параллельное применение термодинамического метода и основных позиций физико-химического анализа, с помощью которого строятся диаграммы состояния, позволяет получить весьма глубокую информацию об изучаемой системе. Однако всегда необходимо помнить, что большей частью рассматриваются лишь равновесные системы. Именно для таких систем изображаются соответствующие диаграммы состояния. Количество и конкретный вид фаз сложной системы, наблюдаемые на практике, могут в действительности сильно отличаться от равновесных, вследствие торможения процесса перехода в равновесное состояние.
[1] Людвиг Больцман (1841 - 1906 г.г.), австрийский физик, один из основоположников статистической физики и физической кинетики.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.158.110 (0.008 с.) |


 и
и  - области твердых растворов. Твердыми растворами называются однородные кристаллические фазы сплавов, у которых атомы растворяемого компонента замещают атомы растворителя в его кристаллической решетке.
- области твердых растворов. Твердыми растворами называются однородные кристаллические фазы сплавов, у которых атомы растворяемого компонента замещают атомы растворителя в его кристаллической решетке. . (6.8)
. (6.8)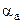 и
и  . Вариантность системы при ТЕ определится:
. Вариантность системы при ТЕ определится: ,
,

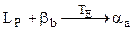 . (6.9)
. (6.9) . (6.10)
. (6.10) , (6.11)
, (6.11)
 . (6.12)
. (6.12)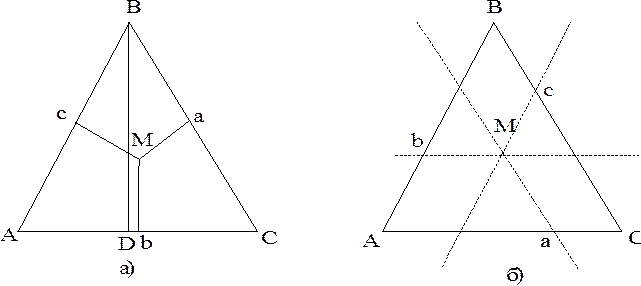

 . (6.10)
. (6.10)


