
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функций для расчетов равновесий.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Этот метод расчета широко используется для вычисления энергетических эффектов химических реакций, констант равновесия химических реакций и т. д. Главное достоинство метода состоит в том, что та часть вычислений, которая требует много времени и является источником наибольших ошибок, сделана единожды и с возможно большей точностью. То, что остается вычислить сверх табличных данных носит большей частью характер поправок, нахождение которых не требует высокой точности и допускает использование разумных приближений. Обычные таблицы содержат величины: - изменения энтальпии при образовании одного моля вещества в стандартных условиях ( - изменения энергии Гиббса образования одного моля вещества в стандартных условиях ( - абсолютных значений энтропии, в расчете на 1 моль вещества в стандартных условиях ( За стандартные условия принято считать температуру 25 0С и давление 1,01 Все подсчеты по таблицам основаны на свойствах аддитивности G, H и S, поэтому сводятся к простому алгебраическому суммированию. аналогичному расчетам по закону Гесса. Так, изменение энтальпии реакции Таблицы термодинамических функций в стандартных условиях позволяют рассчитать Например для расчета энергетического эффекта химической реакции используется уравнение Кирхгофа:
где
Для определения изменения энтропии реакции используется выражение;
где
Если уравнения (5.16) и (5.17) ввести в уравнение:
то получается:
или
По величине
Уравнения (5.18) и (5.19) позволяют вычислять
Следует заметить, что ряд важнейших технологических процессов металлургической практики основан на результатах подобных и аналогичных расчетов. Более того, физическая химия металлургических процессов основана на использовании этих расчетов для анализа схем получения металлов и их сплавов из руд. Приближения Улиха. Первое приближение заключается в том, что
Второе приближение используется тогда, когда нет возможности возпользоваться температурной зависимостью теплоемкости. В этом случае Обычно итоговое уравнение для расчета таково:
где
Метод Темкина - Шварцмана. Если то
где функции f 0(T), f 1(T) и f 2(T) определяются при любой температуре с помощью специальных таблиц. В этом методе расчета его облегчение достигнуто за счет предварительного табулирования всех температурных функций, входящих в уравнение для определения логарифма константы равновесия химической реакции. Владимировым Л.П. были предложены два новых метода простого и быстрого расчета химических равновесий. Первый автором назван приближенным, а второй - точным. В соответствии с приближенным методом расчета для любой химической реакции имеет место простое выражение:
где m и N - численные функции от Особенность точного метода расчета состоит в том, что необходимые для расчета функции заранее вычисляются для простейших соединений, образующихся из элементов. Это дает возможность вычислять логарифм констант равновесия любых сложных реакций путем алгебраического сложения соответствующих каждому реагенту заранее вычисленных функций. Расчет значений логарифмов констант равновесия газовых реакций этим методом производится по вытекающей из точной формулы:
упрощенной формуле:
каждый член которой представляет алгебраическую сумму соответствующих реагентам одной из вышеупомянутых функций ( Функции
Глава VI. Правило фаз. Иллюстрацией практического применения второго закона термодинамики является правило фаз Гиббса (1878 г.), дающее качественную характеристику гетерогенных многофазных равновесных систем. Это правило получило многочисленные подтверждения и разнообразные применения.
1. Основные понятия и определения. Термодинамические системы, представленные телом или группой тел, изолированными от окружающей среды и пребывающие в непрерывном движении бывают гомо- и гетерогенными. Гомогенные системы - системы, внутри которых отсутствуют поверхности раздела, отделяющие друг от друга части системы, отличающиеся свойствами. Гетерогенные системы имеют внутри себя границы раздела, отделяющие части системы, отличающиеся свойствами. Ранее указывалось, что состояние системы определяется совокупностью параметров состояния (Р, Т, V). Фаза (f) - состояние материи, которое повсюду однородно не только по химическому составу, но и по физическим свойствам, - такое определение этому понятию дал Д. У. Гиббс. Фазы бывают твердыми, жидкими и газообразными. Составная часть системы (р) - химически индивидуальные вещества, представляющие систему и способные к самостоятельному существованию вне системы. Например система, образованная тремя химическими соединениями NH4Cl(ТВ), NH3(Г) и НCl(Г) состоит из трех составных частей. Компонент системы (k) - химические индивидуумы, наименьшее число которых необходимо и достаточно для образования всех фаз данной системы. Число компонентов равно числу составных частей за вычетом числа уравнений (r), связывающих составные части. В рассматриваемой системе. состоящей из трех составных частей, возможна реакция вида: NH4Cl(ТВ) поэтому число компонентов будет равно двум: k = p - r = 3 - 1 = 2. Числом степеней свободы (с) называется число независимых термодинамических параметров, определяющих состояние системы. Независимыми являются те параметры, которые можно произвольно задавать или изменять без того,чтобы это влекло за собой изменение других независимых параметров состояния, причем при изменении независимых параметров состояния число фаз в системе не должно изменяться. Чтобы рассчитать число степеней свободы системы нужно из общего числа параметров состояния вычесть число связывающих их уравнений.
Уравнение правила фаз. Пусть рассматриваемая система состоит из f - фаз и k - компонентов, причем каждый из k - компонентов находится в каком-то количестве в каждой из f - фаз. Давление и температура одинаковы для всех фаз данной системы, т.е. имеется два общих параметра состояния. Так как каждый компонент находится в каждой фазе, то возможные концентрации компонентов во всех фазах:
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Число возможных концентраций компонентов составит величину k
Для каждой из фаз имеется свое уравнение состояния. Например, для первой фазы это уравнение таково:
Таких уравнений столько, сколько фаз в системе, т.е. f - штук. Система находится в состоянии термодинамического равновесия, что означает равенство химических потенциалов компонентов (
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Число строк в матрице равно числу компонентов (k), а число столбцов равно (f - 1), тогда общее число уравнений составит: k(f - 1). Таким образом, общее число уравнений, связывающих значения химических потенциалов компонентов вычислится как f + k(f - 1). Согласно определению, число степеней свободы равно разности между общим числом параметров состояния и числом уравнений, связывающих эти параметры: с = (k или с = k - f + 2. (6.4) т. е. число степеней свободы равно разности между числом компонентов и фаз плюс два. В системах без участия в равновесии газообразной фазы, один из параметров, общий для всех фаз системы, а именно давление, не оказывает влияние на равновесие в системе, если изменяется в небольших пределах и поэтому исключается из числа общих параметров состояния. Это положение применимо, в частности, к металлическим расплавам и поэтому уравнение правила фаз записывается в виде: с = k - f + 1. (6.5) Равновесие нонвариантно (безвариантно), если с = 0, моновариантно (одновариантно), если с = 1 и дивариантно (двухвариантно), если с = 2.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.135.132 (0.013 с.) |

 );
); );
);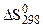 );
); 105 Па.
105 Па. Н равно алгебраической сумме изменений энтальпий образования продуктов реакции. Это относится к
Н равно алгебраической сумме изменений энтальпий образования продуктов реакции. Это относится к  , (5.16)
, (5.16) - изменение энтальпии реакции при температуре Т, причем
- изменение энтальпии реакции при температуре Т, причем  .
. , (5.17)
, (5.17) - изменение энтропии реакции при температуре Т.
- изменение энтропии реакции при температуре Т. ,
, ,
, . (5.18)
. (5.18) согласно уравнению стандартного сродства -
согласно уравнению стандартного сродства -  . (5.19)
. (5.19) . (5.20)
. (5.20) , (5.21)
, (5.21) .
. ,
, , (5.22)
, (5.22) , (5.23)
, (5.23)
 , (5.24)
, (5.24) NH3(Г) + HCl(Г),
NH3(Г) + HCl(Г), - для первого компонента;
- для первого компонента; - для второго компонента;
- для второго компонента; - для k - го компонента. (6.1)
- для k - го компонента. (6.1) . (6.2)
. (6.2)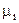 ) во всех фазах системы, т.е.:
) во всех фазах системы, т.е.: - для первого компонента;
- для первого компонента; - для второго компонента;
- для второго компонента; - для k - го компонента. (6.3)
- для k - го компонента. (6.3)


