
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второй закон термодинамики. Биоэнергетика.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
План 2.1. Второй закон термодинамики. Энтропия. 2.2. Свободная энергия Гиббса. 2.3. Биоэнергетика.
Второй закон термодинамики. Энтропия
Химические реакции и физико-химические процессы можно разделить на две группы: самопроизвольные (спонтанные) и несамопроизвольные (неспонтанные). Самопроизвольные процессы протекают без сообщения системе допол-нительной энергии из окружающей среды. Самопроизвольными являются процессы растворения, диффузии, осмоса, расширения газа в пустоту. Пределом протекания самопроизвольных процессов является состояние термодинамического равновесия. Термодинамическое равновесие — это такое состояние системы, в котором ее термодинамические параметры (T, p, V и др.) не изменяются во времени и имеют одинаковое значение во всех точках объема системы. Система, находящаяся в равновесии, не способна выполнять работу. Термодинамическое равновесие достигается только в закрытых и изолированных системах. Оно не достижимо для открытых систем из-за постоянно изменяющихся внешних условий. Для открытых систем аналогом равновесного является стационарное состояние, обусловленное сбалансированностью потоков энергии и вещества в систему и из системы. Стационарное состояние характеризуется длительным постоянством термодинамических параметров системы и одновременной способностью совершать полезную работу. Для протекания несамопроизвольных процессовнеобходимо сообщить системе дополнительную энергию. Например, фотосинтез, протекающий под воздействием УФ излучения.
Рисунок 1 — Схема идеальной тепловой машины
Большой вклад в изучение теории тепловых машин внес французский инженер С. Карно. Теорема Карно: 1) Коэффициент полезного действия тепловой машины, не зависит от рода рабочего тела, а зависит только от температур нагревателя и холодильника. 2) Коэффициент полезного действия тепловой машины всегда меньше единицы (уравнение Карно):
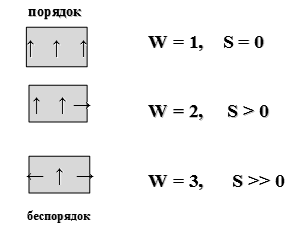
Поскольку Т2 ≠ 0, (абсолютный нуль не достижим), то к.п.д. < 1 Теоретический вывод подтверждается практикой. К.п.д. самых современных тепловых машин невысок: для тепловозов ~ 20%, для двигателей внутреннего сгорания ~30%. К.п.д. превращения химической энергии пищи в организме человека ~ 25%, к.п.д. превращения АТФ в работу мышц ~ 50 %, а к.п.д. здорового сердца составляет ~ 43 %. Формулировки второго закона: 1) Невозможно полностью превратить теплоту в работу (У. Кельвин 1851). 2) Невозможен процесс, единственный результат которого состоял бы в переходе энергии от холодного тела к горячему (Клаузиус, 1865). 3) Самопроизвольные процессы протекают с ростом энтропии. Максимум энтропии достигается в состоянии равновесия (Л.Больцман). Для математического описания второго закона термодинамики используется термодинамическая функция состояния, называемая энтропией (S, Дж/К). Термин «энтропия» был предложен Клаузиусом в 1865. Энтропия (S) — это отношение теплоты, поступающей в систему, к температуре системы: S = Энтропия является единственной функцией состояния, имеющей два толкования: термодинамическое и статистическое. Термодинамическое толкование энтропии: энтропия является характеристикой тепловых потерь системы в данном интервале температур. Она характеризует ту часть теплоты, которая рассеивается в пространстве, не превращаясь в полезную работу. Чем больше энтропия, тем ниже «качество энергии» (меньше к.п.д. процесса). Взаимосвязь энтропии, теплоты и температуры описывается неравенством Клаузиуса: ΔS Статистическое толкование энтропии было предложено Л.Больцманом в 1904 г. Статистическая термодинамика рассматривает энергетическое состояние системы, исходя из состояния ее структурных единиц. Уравнение Больцмана: S = k·ln W, где k — константа Больцмана, равная 1,38×10-23 Дж/K, W — термодинамическая вероятность системы, т.е. число микросостояний, посредством которых реализуется данное макросостояние. Микросостояние – это скорость, энергия, импульс движения и другие характеристики каждой отдельно взятой структурной единицы. Чем меньше число микросостояний, тем выше упорядоченность системы. Так, если все структурные единицы системы имеют одинаковые энергетические характеристики, то термодинамическая вероятность системы равна 1, а энтропия равна 0. Если структурные единицы системы имеют различные энергетические характеристики, то W>1, а S>0 (рисунок 2)
Рисунок 2 — Взаимосвязь термодинамической вероятности системы и ее энтропии Энтропия — количественная мера беспорядка в системе. Чем больше энтропия системы, тем больше беспорядок в ней. Расчет энтропии химической реакции (ΔrS) выполняется на основе закона Гесса. Для условной реакции: аА + bВ → сС + dD, энтропия может быть рассчитана как: ΔrS = c·S (C) + d·S (D) – a·S (A) – b·S (B), где S –мольная энтропия вещества, Дж/моль·К. Если ΔrS > 0 — реакция протекает с увеличением беспорядка; если ΔrS < 0 — реакция протекает с уменьшением беспорядка.
Свободная энергия Гиббса
При протекании химических процессов наблюдаются две противоположные тенденции: (а) стремление отдельных частиц соединится в более крупные агрегаты, что приводит к уменьшению запаса внутренней энергии системы (H → min); (б) стремление агрегатов к разделению на более мелкие частицы, что приводит к увеличению энтропии (S → max). Обе тенденции находят свое отражение в термодинамической функции состояния, называемой свободной энергией Гиббса или изобарно-изотермическим потенциалом (G): G = H – TS DG = DH – TDS Физический смысл свободной энергии Гиббса понятен из совместного рассмотрения первого и второго законов термодинамики:
Q = T·ΔS Отсюда A' = T·DS – DU – p·DV = TDS – (DU + p·DV), где DU + p·DV = DH Следовательно, A' = – (DH – TDS), где DH – TDS = DG Таким образом, A' = – DG Соответственно, DG имеет смысл полезной работы, выполненной в системе или над системой. свободная энергия Гиббса (G) — это часть внутренней энергии системы, способная превращаться в полезную работу. Знак ΔG (+ или –) является критерием возможности протекания самопроизвольных процессов в закрытых системах. Так, если процесс является самопроизвольным, то при его протекании совершается полезная работа (A′ >0); соответственно ∆G < 0. В состоянии термодинамического равновесия полезная работа не выполняется (A′ = 0), следовательно, ∆G = 0. В ходе несамопроизвольного процесса работа выполняется над системой (A′ < 0), соответственно ∆G > 0. Таким образом, самопроизвольно осуществляются те процессы, протекание которых сопровождается уменьшением свободной энергии Гиббса. Характер процесса иногда можно изменять, варьируя термодинамические параметры системы: температуру, давление или концентрацию реагирующих веществ (таблица 2).
Таблица 2 — Влияние температуры на характер процесса
Рассчитав ΔG, можно определить: · характер процесса (само- или несамопроизвольный); · величину полезной работы, совершаемой при протекании самопроизвольного процесса. Способы расчета DG 1. Свободную энергию химической реакции можно рассчитать по уравнению:
ΔrG = ΔrH – ТΔrS, где ТΔrS — энтропийный фактор химической реакции. 2. Свободную энергию химической реакции можно рассчитать на основе закона Гесса: ΔrG = с·ΔfG (C) + d·ΔfG (D) – a·ΔfG (A) – b·ΔfG (B), где ∆fG — свободная энергия образования сложного вещества из простых веществ, kДж/моль. 3. Расчет DG переноса вещества из одной фазы в другую выполняется по уравнению: ΔrG = – ν·R·T·ln где ν — количество переносимого вещества, моль; R — универсальная газовая постоянная, равная 8,31 Дж/моль∙К; СМ1 и CМ2 — концентрации вещества в различных фазах, моль/л (СМ1<CМ2). Данное уравнение можно использовать для расчета осмотической работы, выполняемой почкой.
Биоэнергетика
Биоэнергетика — это раздел термодинамики, изучающий превращения энергии, теплоты и работы в живых системах. С точки зрения биоэнергетики, человек — это открытая стационарная система, главным источником энергии для которой служит химическая энергия пищи (99 %). Энергетические затраты человека обеспечиваются за счет: · углеводов на 55-60%, · жиров на 20-25%, · белков на 15-20%. Получаемая энергия расходуется: · на совершение работы внутренних органов, связанной с дыханием, кровообращением, перемещением метаболитов, секрецией соков и т.д., · на выполнение внешней работы, связанной со всеми перемещениями человека и его трудовой деятельностью, · на нагревание вдыхаемого воздуха, потребляемой воды и пищи. Коэффициент полезного действия превращения химической энергии пищи в организме человека составляет ~ 25 %.Таким образом, энтропийные потери организма составляют 75%. Если сфокусировать теплоту, излучаемую телом человека за сутки, то можно вскипятить 20 л воды. Биохимическими называются химические реакции, протекающие в биосистемах (in vivo). Они могут быть как экзергоническиеми (самопроизвольными) ΔrG < 0, так и эндергоническими (несамопроизвольными) ΔrG > 0. Окисление углеводов и жиров в организме протекает самопроизвольно и сопровождается выделением большого количества энергии: C6H12O6 + 6 O2 → 6 CO2 + 6 H2O, DG = – 2870 кДж C15H31COOH + 23 O2 → 16 CO2 + 16 H2O, DG = – 9790 кДж. пальмитиновая к-та Часть энергии, выделяющаяся при окислении компонентов пищи, накапливается в макроэргических соединениях, таких как АТФ, АДФ, ацетилкофермент A и др. Получение АТФ из АДФ и фосфата описывается уравнением: АДФ + H3PO4 → АТФ + H2O, ∆G = + 30,6 кДж. Реакция протекает несамопроизвольно, поглощая энергию, выделяющуюся при окислении глюкозы в клетках. Энергия, выделяющаяся при окислении одной молекулы глюкозы, достаточна для синтеза 36 молекул АТФ из АДФ и фосфата. Такие реакции называются сопряженными. Принцип энергетического сопряжения состоит в следующем: эндергонические реакции протекают за счет энергии экзергонических реакций. Как правило, сопряженные реакции катализируются общим ферментом.
Схема сопряженной реакции: A + B → C + D, ∆G1 << 0 L + M → P + Q, ∆G2 > 0 ∆Gобщ = ∆G1 + ∆G2 < 0 Таким образом, обе реакции протекают как единый самопроизвольный процесс. Пример энергетического сопряжения. C6H12O6 + 6 O2 → 6 CO2 + 6 H2O, DG = - 2870 кДж 36 (AДФ + H3PO4) → 36 (ATФ + H2O), DG = +1 100 кДж DG общ = - 2870 + 1100 = - 1770 кДж Приведенные данные позволяют рассчитать к.п.д. клетки: выделилось 2870 кДж, аккумулировано 1100 кДж, энтропийные потери 1770 кДж к.п.д = 1100/2870 = 0.38 или 38%. Таким образом, клетка аккумулирует лишь 38% химической энергии глюкозы, а оставшиеся 62% рассеивается в пространстве как теплота. В современной медицине широко применяются методы биоэнергетической диагностики и терапии. К биоэнергетическим методам лечения относятся: иглотерапия, гирудотерапия (лечение медицинскими пиявками), массаж, упражнения по системе Йоги и др.
Лекция 3 ХИМИЧЕСКОЕ РАВНОВЕСИЕ
План 3.1. Кинетическое и термодинамическое описание химического равновесия. 3.2. Смещение химического равновесия (принцип Ле Шателье). 3.3. Равновесия в биологических средах.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 990; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.53.18 (0.014 с.) |

 Рассмотрение вопросов о характере протекания процессов выполняется в рамках второго закона термодинамики. Второй закон термодинамики был сформулирован на основе анализа действия тепловых машин. Тепловая машина – это устройство, в котором тепловая энергия превращается в механическую работу (рисунок 1).
Рассмотрение вопросов о характере протекания процессов выполняется в рамках второго закона термодинамики. Второй закон термодинамики был сформулирован на основе анализа действия тепловых машин. Тепловая машина – это устройство, в котором тепловая энергия превращается в механическую работу (рисунок 1).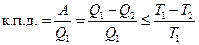
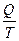
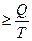
 Q = ΔU + А΄ + p·ΔV
Q = ΔU + А΄ + p·ΔV ,
,


