
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения Колмогорова. Предельные вероятности состоянийСодержание книги Поиск на нашем сайте
Марковские случайные процессы. Определения. МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ - процессы без вероятностного последствия, статистич. свойства к-рых в последующие моменты времени зависят только от значений процессов в данный момент и не зависят от их предыстории. M.с.п. - удобная матем. идеализация разл. случайных процессов, встречающихся в физике. К ним относятся процессы типа броуновского движения, равновесные и неравновесные флуктуации параметров макроскопич. систем, сравнительно медленные изменения амплитуды и фазы сигналов автогенераторов под действием быстро меняющихся естеств. шумов и т. д. Эффективность марковского процесса приближения при рассмотрении реальных случайных процессов обусловлена существованием развитого матем. аппарата для анализа статистич. свойств M.с.п. Тип M.с.п. X(t)определяется тем, к какому множеству принадлежат аргумент t и возможные значения процесса х. Если t и х принимают дискретные значения, X(t)представляет собой марковскую цепь. M.с.п. с непрерывным временем, принимающий значения из дискретного множества Рассмотрим непрерывнозначный M.с.п. с непрерывным временем. Пусть в моменты и
выражающее отсутствие последействия. Условную плотность вероятности
от к-рого можно перейти к кинетич. ур-нию
Здесь
кинетич. коаф., описывающие локальные свойства M.с.п. в момент t в точке х. Для разрывных M.с.п., реализации к-рых скачком меняют значения в случайные моменты времени, кинетич. ур-ния эквивалентны интегро-дифференц. Колмогорова - Феллера уравнениям.
M.с.п., реализации к-рых с вероятностью 1 непрерывны во времени, наз. непрерывными или диффузионными процессами. Для них отличны от нуля только два кинетич. коэф.: коэф. сноса
Если
Статистич. характеристики M. с. п. находят, исследуя решения кинетич. ур-ний с теми или иными начальными и граничными условиями. Так, плотность вероятности переходов процесса Орнштейна - Уленбека, удовлетворяющая ур-нию (1) с начальным условием
равна
Для однородных во времени процессов может существовать стационарная плотность вероятности
удовлетворяющая, в случае диффузионного процесса, обыкновенному дифференц. ур-нию
При анализе M. с. п., реализации к-рых обрываются или отражаются на заданных границах, кинетич. ур-ния дополняют граничными условиями. Реализации M. с. п. с непрерывным временем удовлетворяют дифференц. стохастическим уравнениям. Напр., реализации диффузионного процесса X(t)удовлетворяют ур-нию
здесь
Кинетич. коэф. диффузионного процесса, описываемого ур-нием (2), равны:
Решение. 1. Сгруппируем данные по числу покупателей k, посетивших магазин в течение часа, а результаты представим в виде таблицы:
Вычислим интенсивность потока:
Найдем теоретические частоты по формуле
2. Вычислим наблюдаемое значение критерия Пирсона по формуле
3. По заданному уравнению значимости 4. Поскольку Пример 2. Результаты наблюдения за потоком покупателей в течение 7 дней работы универмага и проведения регистрации покупателей за каждый час представлены в табл. 3.2. Таблица 3.2
Определим интенсивность входящего потока покупателей в расчете на час работы и по критерию Пирсона с уровнем значимости Решение. Используем модели алгоритма. Получим: Решение. 1. Для каждого интервала
2. Вычислим среднее время обслуживания (
3. Найдем теоретические частоты по формуле
4. Вычислим наблюдаемое значение критерия Пирсона по формуле
5. По заданному уровню значимости 6. Сравним, если Пример 4. Результаты наблюдения за работой консультантов специализированного магазина аудио- и видеотехники по времени обслуживания покупателей представлены в табл. 3.4. Таблица 3.4
Определим среднее время
Пример 5. Результаты регистрации входного потока посетителей в течение дня и значения его характеристик приведены в табл. 3.5. Таблица 3.5
По приведенным данным поток посетителей в течение дня не постоянен: в разные часы работы магазина в него заходит разное количество посетителей, причем разность между максимальным и минимальным количеством посетителей, зашедших в магазин в течение часа, весьма существенна (от 100 до 1000 человек). Однако на ограниченном промежутке времени, например в течение часа, поток посетителей может считаться простейшим. Если к тому же длительности интервалов между двумя соседними событиями распределены по закону Пуассона, следовательно, можно вычислить интенсивность потока посетителей для каждого часа работы магазина, а также их среднее значение. Интенсивность потока посетителей в течение дня, как и количество посетителей магазина, является величиной непостоянной и изменяется в пределах от Рассмотрим распределение потока посетителей того же магазина, но уже в течение недели. Динамика потока посетителей представлена в табл. 3.6, в которой значения интенсивности являются усредненными характеристиками потока для каждого дня недели. Таблица 3.6
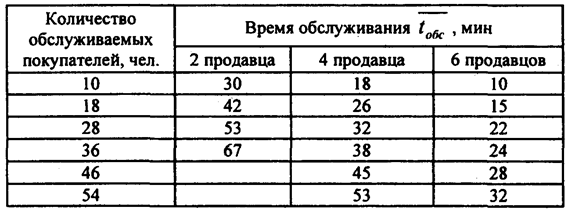
Следует отметить, что максимальные (минимальные) значения интенсивности потока, которые приведены в табл. 3.6 ( Изучение потока посетителей магазина помогает рационально организовать работу СМО, а также работу продавцов и кассиров в течение рабочего дня, добиться более равномерной загрузки торговых работников, повысить эффективность их труда. Рассмотрим характеристики потока обслуживания на примере работы секции по продаже радио- и телеаппаратуры. Результаты хронометража времени обслуживания покупателей разным числом продавцов в магазине представлены в табл. 3.7. Таблица 3.7
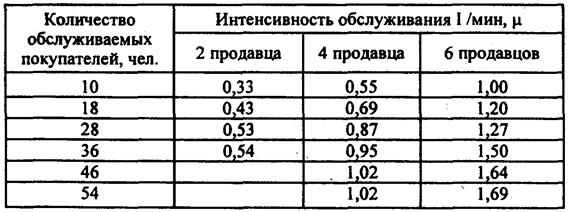
По приведенным данным можно рассчитать интенсивность обслуживания покупателей при различной организации торгового процесса: все продавцы работают как одна бригада и тогда они образуют один канал обслуживания, каждый продавец работает самостоятельно и тогда число каналов обслуживания будет определяться количеством продавцов. Для случая бригадной организации торгового процесса получили следующую интенсивность обслуживания (табл. 3.8). Таблица 3.8
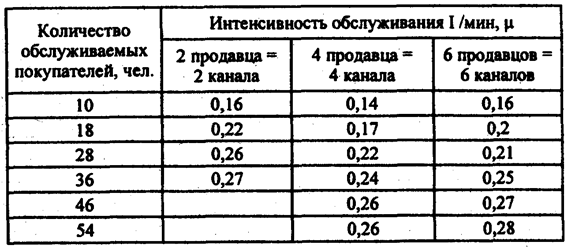
По данным табл. 3.8 с увеличением количества продавцов, образующих канал обслуживания, увеличивается интенсивность обслуживания Для случая, когда каждый продавец работает самостоятельно, получили значения интенсивности обслуживания, которые приведены в табл. 3.9. Таблица 3.9
По данным табл. 3.9 видно, что независимо от количества продавцов интенсивности обслуживания для каждого канала примерно одинаковы, что свидетельствует, в свою очередь, о равномерной загрузке продавцов. Таким образом, изучая входные потоки обслуживания, можно оценить производительность каналов обслуживания, степень их загрузки и разработать рекомендации по рациональной организации работы систем массового обслуживания.
Уравнения Колмогорова. Предельные вероятности состояний Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система
Вероятностью i-го состояния называется вероятность
Рассмотрим систему в момент
1. Система в момент
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью
2. Система в момент
Потоком интенсивностью
Применяя теорему сложения вероятностей, получим
откуда
Переходя к пределу при
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы
Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния Марковские случайные процессы. Определения. МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ - процессы без вероятностного последствия, статистич. свойства к-рых в последующие моменты времени зависят только от значений процессов в данный момент и не зависят от их предыстории. M.с.п. - удобная матем. идеализация разл. случайных процессов, встречающихся в физике. К ним относятся процессы типа броуновского движения, равновесные и неравновесные флуктуации параметров макроскопич. систем, сравнительно медленные изменения амплитуды и фазы сигналов автогенераторов под действием быстро меняющихся естеств. шумов и т. д. Эффективность марковского процесса приближения при рассмотрении реальных случайных процессов обусловлена существованием развитого матем. аппарата для анализа статистич. свойств M.с.п. Тип M.с.п. X(t)определяется тем, к какому множеству принадлежат аргумент t и возможные значения процесса х. Если t и х принимают дискретные значения, X(t)представляет собой марковскую цепь. M.с.п. с непрерывным временем, принимающий значения из дискретного множества Рассмотрим непрерывнозначный M.с.п. с непрерывным временем. Пусть в моменты и
выражающее отсутствие последействия. Условную плотность вероятности
от к-рого можно перейти к кинетич. ур-нию
Здесь
кинетич. коаф., описывающие локальные свойства M.с.п. в момент t в точке х. Для разрывных M.с.п., реализации к-рых скачком меняют значения в случайные моменты времени, кинетич. ур-ния эквивалентны интегро-дифференц. Колмогорова - Феллера уравнениям.
M.с.п., реализации к-рых с вероятностью 1 непрерывны во времени, наз. непрерывными или диффузионными процессами. Для них отличны от нуля только два кинетич. коэф.: коэф. сноса
Если
Статистич. характеристики M. с. п. находят, исследуя решения кинетич. ур-ний с теми или иными начальными и граничными условиями. Так, плотность вероятности переходов процесса Орнштейна - Уленбека, удовлетворяющая ур-нию (1) с начальным условием
равна
Для однородных во времени процессов может существовать стационарная плотность вероятности
удовлетворяющая, в случае диффузионного процесса, обыкновенному дифференц. ур-нию
При анализе M. с. п., реализации к-рых обрываются или отражаются на заданных границах, кинетич. ур-ния дополняют граничными условиями. Реализации M. с. п. с непрерывным временем удовлетворяют дифференц. стохастическим уравнениям. Напр., реализации диффузионного процесса X(t)удовлетворяют ур-нию
здесь
Кинетич. коэф. диффузионного процесса, описываемого ур-нием (2), равны:
|
|||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.63 (0.014 с.) |

 , наз. дискретнозначным марковским процессом. К ним относится, в частности, телеграфный процесс с двумя значениями
, наз. дискретнозначным марковским процессом. К ним относится, в частности, телеграфный процесс с двумя значениями  смена к-рых происходит в случайные моменты времени.
смена к-рых происходит в случайные моменты времени.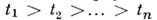 известны значения процесса
известны значения процесса 
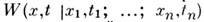 - условная плотность вероятности значений процесса в момент t > t\, тогда справедливо равенство
- условная плотность вероятности значений процесса в момент t > t\, тогда справедливо равенство
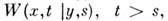 полностью определяющую [вместе с безусловной плотностью вероятности
полностью определяющую [вместе с безусловной плотностью вероятности  все статистич. свойства M.с.п., наз. плотностью вероятности переходов. Она удовлетворяет интегральному уравнению Смолуховского
все статистич. свойства M.с.п., наз. плотностью вероятности переходов. Она удовлетворяет интегральному уравнению Смолуховского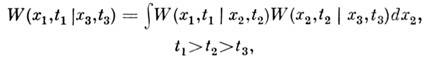

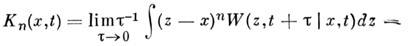
 и коэф. диффузии
и коэф. диффузии 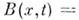
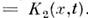 . При этом кинетич. ур-ние переходит в Фоккера - Планка уравнение (см. также Колмогорова уравнения):
. При этом кинетич. ур-ние переходит в Фоккера - Планка уравнение (см. также Колмогорова уравнения): 
 или
или  , то M.с.п. наз. однородным в пространстве или во времени. В последнем случае плотность вероятности переходов зависит лишь от разности времён:
, то M.с.п. наз. однородным в пространстве или во времени. В последнем случае плотность вероятности переходов зависит лишь от разности времён: 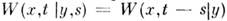 Простейшим однородным в пространстве и во времени непрерывным M. с. п. является винеровский случайный процесс, для к-рого
Простейшим однородным в пространстве и во времени непрерывным M. с. п. является винеровский случайный процесс, для к-рого 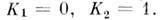 Он описывает, напр., свободную диффузию частиц в среде с пост, темп-рой. Простейшим однородным во времени процессом является процесс Орнштейна- Уленбека, для к-рого
Он описывает, напр., свободную диффузию частиц в среде с пост, темп-рой. Простейшим однородным во времени процессом является процесс Орнштейна- Уленбека, для к-рого 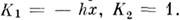 Ур-ние Фоккера - Планка в этом случае имеет вид
Ур-ние Фоккера - Планка в этом случае имеет вид
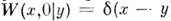 )
)


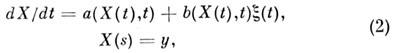
 и-
и-  детерминиров. ф-ции, а-
детерминиров. ф-ции, а- 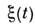 белый шум, для к-рого
белый шум, для к-рого
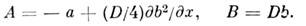





 и числу степеней свободы
и числу степеней свободы  , где
, где  - число групп в ряду (в нашем случае
- число групп в ряду (в нашем случае  ) по таблице значений критических точек
) по таблице значений критических точек 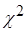 - распределения определим
- распределения определим 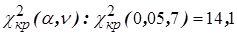 .
.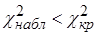 , то можно считать, поскольку в нашем случае это условие выполняется: 12,51 < 14,1, то входящий поток покупателей описывается пуассоновским законом распределения с интенсивностью
, то можно считать, поскольку в нашем случае это условие выполняется: 12,51 < 14,1, то входящий поток покупателей описывается пуассоновским законом распределения с интенсивностью  .
.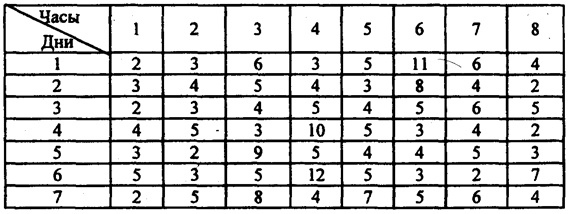
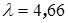 покуп час;
покуп час; 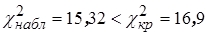 , что свидетельствует о правильном предположении о пуассоновском законе распределения входящего потока покупателей.
, что свидетельствует о правильном предположении о пуассоновском законе распределения входящего потока покупателей. вычислим его середину по формуле
вычислим его середину по формуле

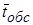 и интенсивность обслуживания
и интенсивность обслуживания  :
: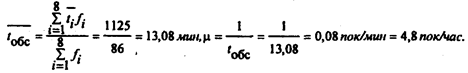
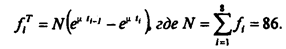


 ) по таблице значений критических точек
) по таблице значений критических точек 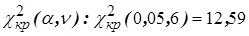 .
.
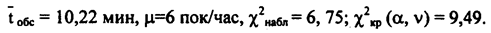

 пок/мин до
пок/мин до 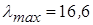 пок/мин, однако эти значения можно усреднить, и тогда получаются следующие значения
пок/мин, однако эти значения можно усреднить, и тогда получаются следующие значения  1 пок/мин до
1 пок/мин до  1 пок/мин. Среднее значение интенсивности потока посетителей в течение дня
1 пок/мин. Среднее значение интенсивности потока посетителей в течение дня 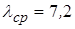 1 пок/мин.
1 пок/мин.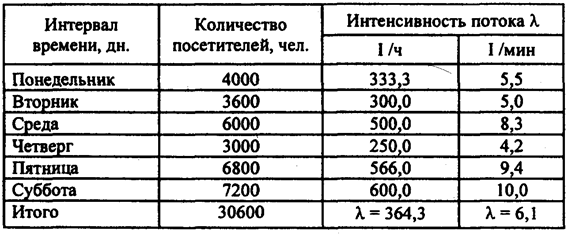
 в
в 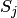 происходят под воздействием простейших потоков событий с интенсивностями
происходят под воздействием простейших потоков событий с интенсивностями 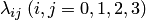 ; так, переход системы из состояния
; так, переход системы из состояния  в
в 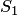 будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния
будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния  имеет четыре возможных состояния:
имеет четыре возможных состояния: 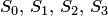 .
.
 того, что в момент
того, что в момент 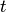 система будет находиться в состоянии
система будет находиться в состоянии 
 , найдем вероятность
, найдем вероятность 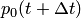 того, что система в момент
того, что система в момент 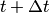 будет находиться в состоянии
будет находиться в состоянии  находилась в состоянии
находилась в состоянии 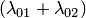 , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной
, т.е. в соответствии с формулой (7), с вероятностью, приближенно равной  . А вероятность того, что система не выйдет из состояния
. А вероятность того, что система не выйдет из состояния 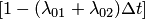 . Вероятность того, что система будет находиться в состоянии
. Вероятность того, что система будет находиться в состоянии 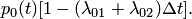
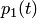 (или
(или 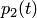 ) находилась в состоянии
) находилась в состоянии 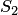 и за время
и за время 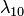 (или
(или  — с- рис. 1) система перейдет в состояние
— с- рис. 1) система перейдет в состояние 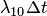 (или
(или  ). Вероятность того, что система будет находиться в состоянии
). Вероятность того, что система будет находиться в состоянии 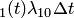 (или
(или  ).
).

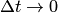 (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную
(приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную  (обозначим ее для простоты
(обозначим ее для простоты 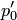 ):
):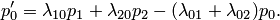
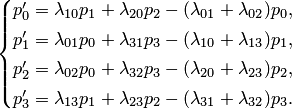
 . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии
. Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии 
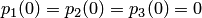 .
. , которые называются предельными (или финальными) вероятностями состояний.
, которые называются предельными (или финальными) вероятностями состояний.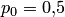 , то это означает, что в среднем половину времени система находится в состоянии
, то это означает, что в среднем половину времени система находится в состоянии 
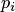 , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.


