
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сущность метода Монте-Карло.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Одним из численных методов, получивших распространение при появлении быстродействующих электронных вычислительных машин (ЭВМ), является метод статистических испытаний, или метод Монте Карло. Он базируется на использовании так называемых случайных чисел — возможных значений некоторой случайной величины с заданным распределением вероятностей. При реализации метода статистических испытаний на ЭВМ случайные числа вырабатываются специальной электронной приставкой к ЭВМ (датчиком случайных чисел) или самой машиной по специальной программе. В любом из этих вариантов для генерирования случайных чисел используется аппаратурная (датчик случайных чисел) или алгоритмическая (специальная программа для ЭВМ) модель некоторого случайного процесса, вероятностные характеристики которого известны или могут быть оценены экспериментально. Ранее, до появления ЭВМ, этой цели служили простейшие случайные процессы, такие, как бросание монеты (выпадение герба или решки с вероятностями Сущность метода статистических испытаний поясним на примерах. В качестве первого примера рассмотрим вычисление площади некоторой фигуры произвольной формы. Остановимся сначала на частном случае решения этой задачи. Пусть требуется вычислить площадь фигуры (см. рис. 1), ограниченной отрезками ОА и
Рис. 1. Пользуясь обычными численными методами для приближенного вычисления искомой площади, поступают следующим образом. Разбивают отрезок (0,1) на оси ОХ на элементарной фигуры приближенно можно заменить площадью соответствующего прямоугольника, равной
Рис. 2. Отметим для дальнейшего, что такой способ определения площади требует вычисления значений функции Посмотрим теперь, как решается эта же задача методом статистических испытаний. Пусть мы имеем случайную величину равномерно распределенную на отрезке [0, 1] (см. [5]). Это значит, что вероятность попадания ее возможных значений Если возможные значения
Рис. 3. Проведем мысленный эксперимент: внутрь единичного квадрата случайным образом с равномерным распределением бросается точка. Это эквивалентно выборке пары чисел Предположим, что количество точек под кривой Если следовать геометрическим соображениям, ясно, что вероятность Р попадания точки в часть квадрата, находящуюся под кривой
Для решения рассмотренного примера на ЭВМ нет необходимости в воспроизведении всех указанных выше действий. Сущность метода статистических испытаний для данного случая состоит в моделировании эксперимента при помощи случайных чисел. Процедура решения выглядит следующим образом: 1. Выбирается случайное число 2. Вычисляется значение рассматриваемой функции 3. Вырабатывается следующее случайное число 4. Количество выработанных таким образом случайных точек (пар случайных чисел) подсчитывается специальным счетчиком, который мы будем называть счетчиком количества испытаний 5. Значение функции
выполнено, что соответствует попаданию случайной точки 6. Полученные значения признака (о прибавляются к содержимому счетчика количества точек под кривой 7. Управление передается снова первой операции, что соответствует переходу к новой случайной точке
Рассмотренная процедура не требует запоминания всех случайных чисел, полученных в результате эксперимента. Запоминаются только значения Точность решения задачи методом статистических испытаний растет с увеличением количества испытаний N и при достаточно больших N становится приемлемой с практической точки зрения. (Этот вопрос будет более обстоятельно выяснен ниже, в § 5.) Целесообразно обратить внимание на ряд возможных обобщений. Во-первых, метод статистических испытаний позволяет вычислять площади фигур произвольной формы и любых размеров. Пусть, например, требуется вычислить площадь
Тогда квадрат АВЕД будет единичным, а искомая площадь
где 5 — площадь фигуры, выраженная в единицах измерения, соответствующих новым масштабам. Величина 5 может быть определена методом статистических испытаний.
Рис. 4. Процедура решения задачи в основном совпадает с рассмотренной выше, за исключением того, что теперь для каждого
причем Если это неравенство выполнено, случайная точка Во-вторых, задача вычисления площади является частным случаем более общей задачи интегрального исчисления. В самом деле, площадь 5 (см. рис. 3) может быть выражена как
поэтому процедура определения площади одновременно является процедурой вычисления интеграла вида (1.4). Напомним, что здесь
Если же это условие не выполнено и пределы интегрирования произвольны, необходимо преобразовать масштабы по осям координат. Например, пусть требуется вычислить интеграл
где максимальное значение
и изменение масштаба по оси у, получим
где
Таким образом, рассматриваемая задача сводитсяс к предыдущей, решаемой с помощью интеграла вида (1.4). 77. Прикладные задачи определения характеристик случайного процесса. Методы решения. Анализ единственности решения задачи оценивания параметров случайного процесса по данным наблюдений начнем с примера. Пример 9.4. Рассмотрим скалярный случайный процесс
где В данном случае вектор
а случайный процесс Предположим, что для оценивания вектора Поскольку изучаемый случайный процесс является гауссовским, то его одномерные функции плотности вероятностей
Оценку параметра
В качестве реализации такой оценки используем функцию [XVII]
Для построения оценок оставшихся неизвестных параметров мы не располагаем никакими данными, кроме оценок математического ожидания и
Эта система состоит из двух уравнений и содержит три неизвестных параметра, т.е. имеет бесчисленное множество решений. Таким образом, по данным наблюдений, представленным множеством Если Заметим, что рассматриваемый скалярный случайный процесс при Для того чтобы сформулировать условие единственности реления задачи оценивания неизвестных параметров случайного процесса по данным наблюдений, напомним, что любой случайный процесс в общем случае не является полностью определенным и при решении различных задач как теоретического, ток и прикладного характера исследователь вынужден ограничиваться использованием конечномерных законов распределений. Совокупность конечномерных законов распределений является более или менее полной характеристикой случайного процесса. При этом, если
содержит исчерпывающую информацию об исходном случайном процессе на множестве Определение 9.1. Пусть
верно тогда и только тогда, когда Интуитивно понятно, что если по данным наблюдений удается определить такую
где
блочный случайный вектор размерности В связи с этим напомним, что функцию
Известно [V], что для выпуклой (дифференцируемой) функции
Пусть
Определив математические ожидания правой и левой частей этого неравенства, приходим к неравенству Иенсена для выпуклой функции:
Теперь можно сформулировать и доказать теорему единственности решения задачи оценивания неизвестных параметров случайного процесса по данным наблюдений. Теорема 9.1. Пусть
где функция Поскольку
или, что то же самое,
где
то последнее неравенство принимает вид
Это неравенство превращается в равенство тогда и только тогда, когда
Поэтому из неравенства (9.31) и условия теоремы получаем, что для любых
или, что то же самое,
Таким образом, функция Доказанную теорему можно использовать для решения практических задач даже в тех случаях, когда вид Рассмотрим этот случай, поскольку он чаще других встречается в приложениях. Будем считать, что
Для того чтобы выяснить достаточность зтих данных для однозначного оценивания неизвестных параметров, рассмотрим следующую функцию плотности вероятностей
и введем множества
При выполнении условий теоремы 9.1 при любых
т.е. с учетом определения функции
или
Однако по условию задачи вид функции плотности вероятностей Определение 9.2. Будем говорить, что функции
Теорема 9.2. Пусть математическое ожидание
где
Доказательство теоремы 9.2 опирается на следующее утверждение. Лемма 9.1. Пусть
Докажем, что
Действительно,
где
Поскольку
то очевидны равенства
При этом
т.е. при любых то
Теперь вернемся к доказательству теоремы 9.2. Функция
при
и в соответствии с леммой 9.1 каждое слагаемое в правой части (9.32) достигает максимума, поскольку Этот максимум является единственным, т.е. для любого a G В, такого, что
так как функции
а значит, для соответствующих ему слагаемых в суммах неравенства (9.33) будем иметь
Поэтому для любого
а следовательно,
Итак, в ряде случаев, нередко встречающихся в приложениях, единственность решения задачи оценивания неизвестных параметров изучаемого случайного процесса по данным наблюдений можно проверить непосредственно на основании полученных теоретических результатов. Из теоремы 9.2 вытекает весьма важное следствие, состоящее в том, что в тех случаях, когда конечномерные функции плотности вероятностей исходного случайного процесса неизвестны, для решения задачи оценивания можно использовать функции плотности вероятностей нормального закона распределения. Вопрос о том, как повлияет замена неизвестного конечномерного закона распределения изучаемого случайного процесса соответствующим нормальным законом распределения на качество оценок неизвестных параметров, пока оставим открытым и вернемся к нему при рассмотрении квазиправдоподобных оценок. Прежде чем перейти к анализу методов оценивания неизвестных параметров изучаемых случайных процессов, отметим, что пример 9.4 наглядно иллюстрирует идею метода моментов [XVII]. Эта идея состоит в том, что для нахождения оценок неизвестных параметров исходного случайного процесса составляют систему уравнений путем приравнивания теоретических моментов, являющихся функциями неизвестных параметров, к соответствующим статистическим моментам, которые являются функциями данных наблюдений. Метод моментов далее мы рассматривать не будем.
|
||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.01 с.) |

 ) бросание игральной кости
) бросание игральной кости  извлечение карт из тщательно перетасованной колоды
извлечение карт из тщательно перетасованной колоды  вращение рулетки и т. д.
вращение рулетки и т. д. на осях прямоугольных координат ОХ и ОУ, кривой
на осях прямоугольных координат ОХ и ОУ, кривой  и ординатой
и ординатой  (искомая площадь на рис. 1 заштрихована), причем будем считать выполненным условие
(искомая площадь на рис. 1 заштрихована), причем будем считать выполненным условие  для всех
для всех 

 равных частей длиной
равных частей длиной  Искомую площадь 5 представляют в виде суммы площадей
Искомую площадь 5 представляют в виде суммы площадей  элементарных фигур, как показано на рис. 2. Площадь каждой
элементарных фигур, как показано на рис. 2. Площадь каждой где
где  некоторая точка на оси
некоторая точка на оси  внутри
внутри  интервала. Точки
интервала. Точки  выбирают таким образом, чтобы площадь - прямоугольника была возможно более близкой к площади элементарной фигуры. Очевидно, что при достаточно большом
выбирают таким образом, чтобы площадь - прямоугольника была возможно более близкой к площади элементарной фигуры. Очевидно, что при достаточно большом  точность вычисления площади можно сделать вполне приемлемой.
точность вычисления площади можно сделать вполне приемлемой.
 точках.
точках. в интервал
в интервал  пропорциональна длине интервала и не зависит от местоположения его на отрезке [0, 1].
пропорциональна длине интервала и не зависит от местоположения его на отрезке [0, 1]. равномерно распределенной случайной величины
равномерно распределенной случайной величины  заполняют отрезок [0, 1] на оси
заполняют отрезок [0, 1] на оси  и возможные значения у случайной величины
и возможные значения у случайной величины  ) заполняют тот же отрезок на оси
) заполняют тот же отрезок на оси  то пары чисел
то пары чисел  определяют случайную точку
определяют случайную точку  на плоскости
на плоскости  имеющую равномерное распределение в квадрате (0,0), (0,1), (1,1), (1,0), который мы в дальнейшем будем называть единичным квадратом. Это значит, что вероятность попадания точки
имеющую равномерное распределение в квадрате (0,0), (0,1), (1,1), (1,0), который мы в дальнейшем будем называть единичным квадратом. Это значит, что вероятность попадания точки  в некоторую область а пропорциональна площади этой области и не зависит от расположения ее внутри единичного квадрата.
в некоторую область а пропорциональна площади этой области и не зависит от расположения ее внутри единичного квадрата.
 являющихся возможными значениями
являющихся возможными значениями  соответственно. После N таких испытаний (где N достаточно велико) на плоскости появится N случайно расположенных точек, равномерно распределенных в единичном квадрате (см. рис. 3).
соответственно. После N таких испытаний (где N достаточно велико) на плоскости появится N случайно расположенных точек, равномерно распределенных в единичном квадрате (см. рис. 3). равно
равно  над кривой
над кривой  равно
равно  (точки, попадающие точно на кривую, будем считать находящимися под кривой).
(точки, попадающие точно на кривую, будем считать находящимися под кривой). равна отношению площади
равна отношению площади  этой части квадрата к площади всего квадрата. Частота
этой части квадрата к площади всего квадрата. Частота  попадания точки в часть квадрата под кривой
попадания точки в часть квадрата под кривой  при достаточно большом
при достаточно большом  близка к вероятности Р (см. [5]). Отсюда следует, что в качестве приближенного значения искомой площади можно взять частоту
близка к вероятности Р (см. [5]). Отсюда следует, что в качестве приближенного значения искомой площади можно взять частоту  т. е.
т. е.
 из отрезка [0; 1] с равномерным законом распределения (из таблиц случайных чисел или вырабатывается самой машиной с помощью датчика случайных чисел); это случайное число принимается в качестве координаты случайной точки
из отрезка [0; 1] с равномерным законом распределения (из таблиц случайных чисел или вырабатывается самой машиной с помощью датчика случайных чисел); это случайное число принимается в качестве координаты случайной точки  на оси
на оси 
 в точке
в точке 
 принимаемое в качестве координаты точки
принимаемое в качестве координаты точки  на оси О У; таким образом и
на оси О У; таким образом и  определяют случайную точку на плоскости внутри единичного квадрата.
определяют случайную точку на плоскости внутри единичного квадрата.
 сравнивается со случайным числом
сравнивается со случайным числом  Если неравенство (см. рис. 3)
Если неравенство (см. рис. 3)
 в часть квадрата под кривой
в часть квадрата под кривой  то результату сравнения присваивается специальный признак
то результату сравнения присваивается специальный признак  если не выполнено
если не выполнено 

 После проведения N таких экспериментов определяется приближенное значение площади под кривой:
После проведения N таких экспериментов определяется приближенное значение площади под кривой:
 и N. Это немаловажное обстоятельство вообще характерно для реализации метода статистических испытаний на ЭВМ.
и N. Это немаловажное обстоятельство вообще характерно для реализации метода статистических испытаний на ЭВМ. фигуры, изображенной на рис. 4. Поскольку прямоугольник АВЕД не является единичным, целесообразно изменить масштаб по осям координат:
фигуры, изображенной на рис. 4. Поскольку прямоугольник АВЕД не является единичным, целесообразно изменить масштаб по осям координат:
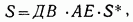

 нужно вычислять два значения
нужно вычислять два значения  ординат точек, лежащих на границе фигуры (см. рис. 4), и проверять справедливость неравенства
ординат точек, лежащих на границе фигуры (см. рис. 4), и проверять справедливость неравенства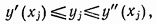
 выбирается уже не из отрезка [0,1], а из преобразованного (сдвинутого) единичного отрезка.
выбирается уже не из отрезка [0,1], а из преобразованного (сдвинутого) единичного отрезка. находится внутри контура фигуры и тогда
находится внутри контура фигуры и тогда 

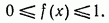

 в отрезке [а, Ь] равно
в отрезке [а, Ь] равно  Используя замену переменных
Используя замену переменных



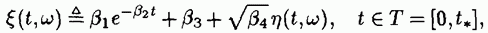





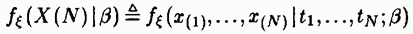




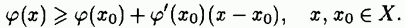







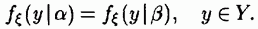


 -мерной функции плотности вероятностей изучаемого случайного процесса неизвестен, а на множестве определены лишь его математическое ожидание и ковариационная матрица как функции неизвестных параметров.
-мерной функции плотности вероятностей изучаемого случайного процесса неизвестен, а на множестве определены лишь его математическое ожидание и ковариационная матрица как функции неизвестных параметров. при
при  содержат все интересующие нас параметры. Это означает, что вся интересующая нас информация об изучаемом случайном процессе представлена в совокупности его одномерных функций плотности вероятностей
содержат все интересующие нас параметры. Это означает, что вся интересующая нас информация об изучаемом случайном процессе представлена в совокупности его одномерных функций плотности вероятностей  Отсюда следует, что для решения задачи оценивания его неизвестных параметров вполне подходит случайная выборка, соответствующая множеству
Отсюда следует, что для решения задачи оценивания его неизвестных параметров вполне подходит случайная выборка, соответствующая множеству  функция плотности вероятностей которой определена равенством (9.18):
функция плотности вероятностей которой определена равенством (9.18):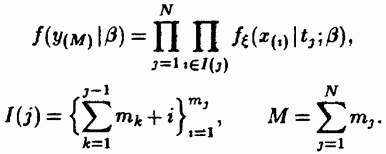
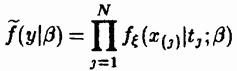

 имеем
имеем 




 неизвестен. Тем не менее, задачу можно решить, если в качестве
неизвестен. Тем не менее, задачу можно решить, если в качестве  использовать плотность нормального закона распределения и наложить на функции
использовать плотность нормального закона распределения и наложить на функции  дополнительные ограничения.
дополнительные ограничения. разделяют точки множества В на множестве
разделяют точки множества В на множестве  , если для любых
, если для любых  существует хотя бы одно значение
существует хотя бы одно значение  такое, что
такое, что
 и ковариационная матрица
и ковариационная матрица  -мерного случайного процесса
-мерного случайного процесса  зависящего от
зависящего от  -мерного вектора неизвестных параметров
-мерного вектора неизвестных параметров  , разделяют точки множества В на множестве
, разделяют точки множества В на множестве  . Тогда задача оценивания неизвестного вектора параметров
. Тогда задача оценивания неизвестного вектора параметров  имеет единственное решение, определяемое условием
имеет единственное решение, определяемое условием

 — плотность нормального распределения:
— плотность нормального распределения: 

 — неизвестная истинная одномерная функция плотности вероятностей случайного процесса.
— неизвестная истинная одномерная функция плотности вероятностей случайного процесса. —
—  -мерный случайный вектор с функцией плотности вероятностей
-мерный случайный вектор с функцией плотности вероятностей  математическим ожиданием
математическим ожиданием  и ковариационной матрицей
и ковариационной матрицей  — плотность распределения вероятностей
— плотность распределения вероятностей  -мерного случайного вектора, распределенного по нормальному закону с математическим ожиданием то и ковариационной матрицей Е. Тогда для любых то
-мерного случайного вектора, распределенного по нормальному закону с математическим ожиданием то и ковариационной матрицей Е. Тогда для любых то  и
и  таких, что то
таких, что то 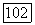 , верно неравенство
, верно неравенство

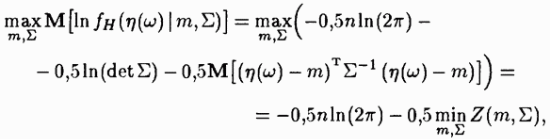

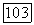 тогда и только тогда, когда
тогда и только тогда, когда  Таким образом, функция
Таким образом, функция  достигает минимума при
достигает минимума при  . А так как, согласно свойствам следа для произведения согласованных матриц, верно представление
. А так как, согласно свойствам следа для произведения согласованных матриц, верно представление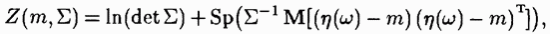

 тогда и только тогда, когда
тогда и только тогда, когда  Таким образом,
Таким образом,
 имеем
имеем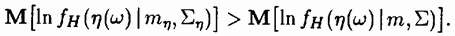

 достигает максимума, так как при
достигает максимума, так как при 

 — функция плотности вероятностей нормального закона распределения.
— функция плотности вероятностей нормального закона распределения. имеем
имеем 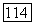

 определены на множестве
определены на множестве 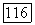 единственным образом и при а
единственным образом и при а  всегда найдется хотя бы один момент времени
всегда найдется хотя бы один момент времени  такой, что
такой, что

 , такого, что а
, такого, что а  имеем
имеем




