
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фазовое равновесие в однокомпонентной системе. Диаграммы состояния однокомпонентных системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основной закон фазового равновесия, часто называемый правилом фаз Гиббса, является одним из важных применений второго начала термодинамики к изучению превращение в гетерогенных системах, в которых возможны переходы вещества из одной фазы в другую (агрегатные превращения, растворение твердых веществ, перераспределение твердого вещества между двумя растворителями и др.). Соотношение С = К ─ Ф + 2 (1.6) называется правилом фаз Гиббса: число степеней свободы (С) равновесной термодинамической системы, на которую влияют только температура и давление, равно числу независимых компонентов (К) системы минус число фаз (Ф) плюс два. Если на равновесие в системе, кроме температуры и давления, могут влиять другие внешние факторы, например, электрические и магнитные поля, поле тяготения и т.д., то в уравнении (1.6) число внешних факторов (n) будет больше двух:
С = К ─ Ф + n (1.7)
В однокомпонентных системах фазы состоят из одного вещества (компонента) в различных агрегатных состояниях. Согласно правилу фаз Гиббса при К=1 число степеней свободы будет равно:
С = 1 ─ Ф + 2 = 3 ─ Ф (1.8)
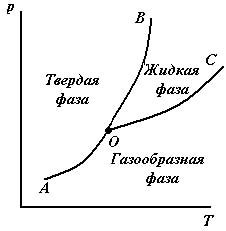
Таким образом, число равновесных фаз в однокомпонентной системе не может быть больше трѐх, т.е. могут существовать системы: однофазные, двухфазные и трѐхфазные. Диаграмма, выражающая зависимость состояния системы и фазовых равновесий в ней от внешних условий или от еѐ состава, называется диаграммой состояния или фазовой диаграммой. На рис.1.1 и рис.1.2 приведены фазовые диаграммы состояния различных однокомпонентных систем.
Три кривые разбивают диаграмму на поля, каждое из которых отвечает одному агрегатному состоянию вещества: твердое, жидкое и газообразное. Кривые отвечают равновесию между соответствующими двумя фазами. Кривая ОС ─ характеризует зависимость давления насыщенного пара над жидкостью и называется кривой испарения; кривая ОВ ─ зависимость температуры плавления (замерзания) жидкости от внешнего давления и называется кривой плавления; кривая ОА ─ зависимость давления насыщенного пара над твердым веществом от температуры и называется кривой возгонки, кривая OD определяет давление насыщенного пара над переохлажденной водой (метастабильное состояние). Эти же кривые характеризуют и обратные равновесные соответствующие процессы: конденсации, кристаллизации и сублимации. Все кривые на диаграммах можно описать с помощью уравнения Клапейрона - Клаузиуса (1.13). В процессе плавления (кривая ОВ, рис.1.1), объем образующейся жидкой фазы больше объема твердой фазы и производная давления по температуре положительная, поэтому с увеличением давления температура плавления увеличивается. На рис.1.2 показан процесс плавления, в котором объем твердой фазы больше объема жидкой фазы и производная, это значит, что с ростом давления температура плавления вещества уменьшается (кривая ОВ, рис.1.2). Таким свойством обладает только небольшое число веществ, например, вода, висмут, сурьма, чугун. В процессе испарения (кривая ОС на рис. 1.1 и 1.2) производная положительная, поэтому при повышении давления температура кипения всегда увеличивается. Точка О называется тройной точкой, т.к. в ней могут находиться в равновесии одновременно три фазы: твердая, жидкая и газообразная. Число степеней свободы в тройной точке равно С = 3 ─ Ф = 3 ─ 3= 0, это значит, что нельзя изменять ни один из параметров, иначе состояние равновесия в системе изменится. Давление, которое молекулы пара, находящегося в равновесии с жидкой фазой, оказывают на стенки сосуда и на поверхность жидкости, называется давлением насыщенного пара (для краткости давление пара жидкости). Согласно правилу фаз система с одним компонентом и двумя сосуществующими фазами имеет только одну степень свободы С = 3 ─ Ф = 3 ─ 2 = 1. Следовательно, в процессе испарения можно произвольно изменять один из параметров (либо температуру, либо давление) и при этом не изменится число и природа фаз. Давление пара над поверхностью стабильного химического вещества (жидкости или твердого тела) определяется только температурой и не зависит от количества взятого вещества, от количества пара и от наличия и концентрации воздуха или другого газа, инертного по отношению к другому пару.
Уравнение Клапейрона - Клаузиуса для процесса парообразования Рассмотрим закономерности, связанные с превращением одной фазы чистого вещества в другую. При равновесии между двумя фазами должно выполняться условие:
Где
Подставим уравнения (1. 10) в условие равновесия (1.9):
Преобразуем полученное выражение:
Для обратимых изотермических переходов выполняется:
где Подставляя значение
Уравнение (1.13) называется уравнением Клапейрона - Клаузиуса и используется для описания термодинамики любых равновесных фазовых переходов. В уравнении (1.13) величины имеют следующую размерность: ─ теплота фазового перехода, Дж/моль; изменение молярного объема при переходе из одной фазы в другую, При испарении жидкого вещества или возгонке твердого вещества уравнение (1.13) можно упростить, сделав следующие допущения:
1) Vп>>Vж,, т (Vп ─ молярный объем пара, V ж, т ─ молярный объем жидкого или твердого вещества), поэтому можно пренебречь в знаменателе уравнения (1.13) величиной V ж, т, то есть объемом жидкости, тогда V п─ V ж, т= V п;
2) пар подчиняется уравнению состояния идеального газа, поэтому для 1 моль вещества можно записать:
Подставим уравнение (1.14) в (1.13) и получим новое выражение:
С учетом данных допущений уравнение Клапейрона - Клаузиуса (1.15) принимает вид
где
3) теплота испарения (теплота возгонки) является постоянной величиной, т.е. не зависит от температуры.
Уравнение (1.16) после интегрирования (неопределенный интеграл) при постоянных величинах
где A и В ─ постоянные интегрирования. Величина В зависит от размерности, в которой выражено давление (правильно в Па, приемлемо в атм. или в мм рт.ст.). Уравнение (1.17) часто применяют для определения теплоты парообразования (испарения) графическим способом, поскольку оно имеет вид уравнения прямой. Для удобства построения графика уравнение (1.17) преобразуют к виду:
Уравнение (1.18) отвечает линейной зависимости
Рис.1.3. Линейная зависимость ln p легколетучего вещества от T/ 1000
. По тангенсу угла наклона прямой линии (рис.1.3) можно определить теплоту фазового перехода, так как, где ─ угол, образованный прямой и осью абсциссы. Отсюда теплота парообразования равна:
Тангенс угла наклона прямой линии вычисляется как отношение длины противолежащего катета (а) к длине прилежащего катета (b), взятых в абсолютных величинах согласно масштабу полученного графика на рис 1.3:
Этот способ определения теплоты фазового перехода называют аналитическим. Наиболее грубым допущением из трех, принятых нами при выводе уравнения (1.16), является предположение о независимости от температуры. Однако, учитывая, что при низких давлениях теплота парообразования мало зависит от температуры, в первом приближении можно допустить, что Для многих недиссоциированных легколетучих жидкостей отношение Экспериментальная часть
1. Определение теплоты парообразования легколетучей жидкости Цели работы: 1. Изучить зависимость давления насыщенного пара легколетучей жидкости от температуры. 2. Вычислить теплоту парообразования легколетучей жидкости на основании опытных данных графическим и аналитическим способом. 3. Рассчитать изменение энтропии в процессе испарения исследуемой жидкости.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 4125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |


 ; (1.9)
; (1.9) - химический потенциал соответствующей фазы. Для обратимых процессов можно написать выражения для химического потенциала одного моля чистого вещества в первой и второй фазах:
- химический потенциал соответствующей фазы. Для обратимых процессов можно написать выражения для химического потенциала одного моля чистого вещества в первой и второй фазах: +
+  ;
; +
+  ; (1.10)
; (1.10) +
+  +
+  ; (1.12)
; (1.12) ; (1.12)
; (1.12) теплота фазового перехода; Т ─ температура фазового перехода.
теплота фазового перехода; Т ─ температура фазового перехода.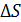 в уравнение (1.12), получаем выражение:
в уравнение (1.12), получаем выражение:
 ; (1.13)
; (1.13)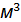 /моль, производная указывает на соотношение изменения температуры и изменения давления при сохранении равновесия между обеими фазами, Па/К.
/моль, производная указывает на соотношение изменения температуры и изменения давления при сохранении равновесия между обеими фазами, Па/К. ; (1.14)
; (1.14) ; (1.15)
; (1.15)
 ; (1.16)
; (1.16) - теплота испарения или теплота возгонки.
- теплота испарения или теплота возгонки. + B; (1.17)
+ B; (1.17) + B; (1.18)
+ B; (1.18) от
от  , представленной на рис. 1.3.
, представленной на рис. 1.3. ; (1.19)
; (1.19)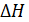 является постоянной величиной и мало отличается от величины при стандартных условиях (=1 атм и =298 К).
является постоянной величиной и мало отличается от величины при стандартных условиях (=1 атм и =298 К). приблизительно равно (88±4) Дж/моль·К (константа Трутона). Значительные положительные отклонения от этой величины указывают на заметную ассоциацию молекул.
приблизительно равно (88±4) Дж/моль·К (константа Трутона). Значительные положительные отклонения от этой величины указывают на заметную ассоциацию молекул.


