
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второе начало термодинамики для фазовых превращенийСодержание книги
Поиск на нашем сайте
Одним из важнейших свойств жидкого вещества является давление его насыщенного пара, характеризующее способность жидкого вещества к испарению. Тепловое движение молекул ведет к отрыву их от поверхности жидкости и переходу в газовую фазу. Однако такой отрыв может произойти, если кинетическая энергия молекулы будет больше энергии взаимной связи с молекулами жидкости. Часть молекул, оторвавшихся от поверхности жидкости, впоследствии снова конденсируется, другая же часть остается в газообразной фазе. Таким образом, на поверхности жидкости всегда происходит одновременно два процесса: испарение и конденсация. Если процессы испарения и конденсации осуществляются в замкнутом пространстве, то скорости этих процессов выравниваются, и между жидкой и газообразной фазами наступает состояние динамического равновесия. Второе начало термодинамики позволяет определить, в каком направлении будет в действительности протекать процесс, когда и при каких условиях установится состояние равновесия между паром и жидкостью, и как температура и давление влияют на это состояние равновесия. Математическое выражение второго закона термодинамики имеет вид: для обратимых процессов
для необратимых процессов
где S ─ некоторая функция состояния, введенная Клаузиусом и названная энтропией. Энтропия ─ величина экстенсивная, т.е. зависящая от количества вещества в системе. Энтропия подчиняется закону аддитивности, т.е. энтропия равновесной термодинамической системы равна сумме энтропии отдельных еѐ частей. Изменение энтропии в сложном процессе равно сумме изменений энтропии в отдельных стадиях процесса. Энтропия является функцией состояния, т.е. еѐ изменение не зависит от пути процесса (обратимый он или необратимый), а определяется начальным и конечным состоянием системы. Поэтому в основе расчета изменения энтропии лежит соотношение (1.1) для обратимого процесса, которое для конечного превращения от состояния 1 до состояния 2 следует проинтегрировать:
где S 1 и S 2 ─ энтропии соответственно начального и конечного состояний. Процессы фазовых превращений (плавление, испарение, возгонка, полиморфные превращения и др.) протекают при постоянной температуре. Равновесное проведение этих процессов требует также и сохранения постоянного давления. Поэтому для изотермического процесса (Т= const) получаем:
При постоянном давлении и тогда изменение энтропии фазового перехода определяется по уравнению:
где
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.166.34 (0.006 с.) |

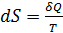 (1.1)
(1.1) (1.2)
(1.2)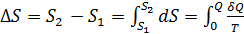 ; (1.3)
; (1.3) ; (1.4)
; (1.4) ; (1.5)
; (1.5) теплота фазового перехода;
теплота фазового перехода;  ─ абсолютная температура фазового перехода.
─ абсолютная температура фазового перехода.


