
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение параметров эмпирической формулы (регрессионный анализ)Содержание книги
Поиск на нашем сайте Одной из широко распространенных задач обработки данных является представление их совокупности некоторой функцией у(х). Задача регрессии заключается в получении таких параметров этой функции, чтобы функция приближала облако исходных точек с наименьшей среднеквадратичной погрешностью. Чаще всего используется линейная регрессия, при которой функция у(х) имеет вид Если вид эмпирической формулы выбран, то возникает задача определения наилучших коэффициентов (параметров), входящих в эту формулу. В общем виде эта задача ставится следующим образом: пусть данная система значений
где Если значение (
Однако на практике значения (
являются возможно малыми по абсолютной величине. Геометрически задача сводится к проведению кривой вида (4), наиболее тесно примыкающей к данной системе точек. Наиболее распространёнными являются эмпирические формулы, линейно зависящие от параметров, т.е. формулы вида
В этом случае система (5) линейная и исследование её сравнительно просто. При нелинейной зависимости в (4) от параметров Рассмотрим три наиболее употребительных метода определения параметров эмпирической формулы: метод выбранных точек; метод средних и метод наименьших квадратов. Метод выбранных точек Пусть для системы опытных данных
содержащая m (m<n) свободных параметров На координатной плоскости Oxy с возможной аккуратностью проводим плавную кривую Г, наиболее близко примыкающую к точкам
Для случая квадратичной зависимости
Заметим, что метод выбранных точек содержит геометрические построения, допускающие известный произвол, и поэтому является грубым. К нему следует прибегать в тех случаях, когда точность исходных данных относительно невелика. Для увеличения точности метода рекомендуется пользоваться сеткой с мелкими делениями. Достоинство метода – простота применения и наглядность. Метод средних Если в эмпирическую формулу
подставить исходные данные
называются уклонениями и представляют собой расстояния по вертикали точек Согласно методу средних за наилучшее положение эмпирической кривой К принимается то, для которого равна нулю алгебраическая сумма Е всех уклонений
Для определения по методу средних постоянных Решив эту систему, найдём коэффициенты Метод наименьших квадратов Пусть известен вид эмпирической формулы
и Согласно методу наименьших квадратов наилучшими коэффициентами
будет минимальной. Отсюда, используя необходимые условия экстремума функции нескольких переменных, получаем так называемую нормальную систему для определения коэффициентов
Если система (10) единственное решение, то оно будет искомым. Система (10) упрощается, если эмпирическая функция
где
Отсюда
Введя сокращенные обозначения
В частном случае, если эмпирическая функция представляет полином
Следовательно, нормальная система (11’) будет иметь вид
Метод наименьших квадратов обладает тем преимуществом, что если сумма S квадратов уклонений Недостатком метода наименьших квадратов является громоздкость вычислений. Поэтому к нему прибегают обычно при обработке наблюдений высокой точности, когда нужно получить также весьма точные значения параметров. Заметим, что в этом случае промежуточные вычисления нужно проводить с надлежащим количеством десятичных знаков, так как в противном случае при неблагоприятных условиях искомые коэффициенты будут иметь мало верных знаков. Но грубые значения этих коэффициентов могут быть получены значительно проще, т.е. применение метода не будет оправданно. В частности, если происходит потеря цифр при вычитании, то вычисления должны быть проведены с достаточным количеством запасных верных значащих цифр. Здесь следует руководствоваться следующим правилом: если численные значения коэффициентов желательно иметь с m верными значащими цифрами и если предварительные вычисления показывают, что первые p цифр исчезнут при вычитании, то вычисления должны быть произведены с m + p + 1 верными значащими цифрами на всех стадиях работы.
|
||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 и описывает отрезок прямой. К линейной регрессии можно свести многие виды нелинейной регрессии при двухпараметрических зависимостях у(х).
и описывает отрезок прямой. К линейной регрессии можно свести многие виды нелинейной регрессии при двухпараметрических зависимостях у(х). приближённо описывается формулой вида
приближённо описывается формулой вида (4)
(4) известная функция и
известная функция и 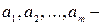 неизвестные постоянные, число которых m обычно меньше числа точек
неизвестные постоянные, число которых m обычно меньше числа точек  , т.е. m < n. Требуется определить эти постоянные.
, т.е. m < n. Требуется определить эти постоянные. ) точно связаны зависимостью (4), то параметры
) точно связаны зависимостью (4), то параметры  могут быть найдены из системы уравнений
могут быть найдены из системы уравнений
 (5)
(5) ) содержат неизбежные ошибки, а число уравнений системы (5) значительно больше числа неизвестных. Поэтому система (5), как правило, является несовместной. Приходится отыскивать наилучшие значения
) содержат неизбежные ошибки, а число уравнений системы (5) значительно больше числа неизвестных. Поэтому система (5), как правило, является несовместной. Приходится отыскивать наилучшие значения 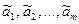 , приближённо удовлетворяющие системе (5), т.е. такие, что невязки (уклонения)
, приближённо удовлетворяющие системе (5), т.е. такие, что невязки (уклонения)


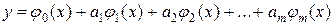
 построена эмпирическая формула
построена эмпирическая формула (6)
(6) , где
, где  . На кривой Г выбираем систему m (по числу параметров) точек
. На кривой Г выбираем систему m (по числу параметров) точек  , не обязательно совпадающих с точками
, не обязательно совпадающих с точками  были по возможности равномерно распределены по всей рабочей части кривой Г и возможно дальше отстояли друг от друга, и в то же время не лежали бы слишком близко к мало надёжным концевым точкам
были по возможности равномерно распределены по всей рабочей части кривой Г и возможно дальше отстояли друг от друга, и в то же время не лежали бы слишком близко к мало надёжным концевым точкам  и
и  . Для удобства обычно берут абсциссы
. Для удобства обычно берут абсциссы  этих точек совпадающими с крупными делениями оси Ox координатной сетки. После этого со всей тщательностью замеряют координаты
этих точек совпадающими с крупными делениями оси Ox координатной сетки. После этого со всей тщательностью замеряют координаты  . Тогда параметры
. Тогда параметры  , в общем случае, могут быть определены из системы m уравнений
, в общем случае, могут быть определены из системы m уравнений

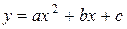 коэффициенты a, b и c определяются из системы трёх уравнений
коэффициенты a, b и c определяются из системы трёх уравнений
 (7)
(7) , то левая часть формулы, вообще говоря, не будет равна правой. Разности (невязки)
, то левая часть формулы, вообще говоря, не будет равна правой. Разности (невязки)

 от графика эмпирической функции (7), взятые со знаком плюс (+) или со знаком минус (-).
от графика эмпирической функции (7), взятые со знаком плюс (+) или со знаком минус (-). , т.е. должно иметь место равенство
, т.е. должно иметь место равенство (8)
(8) , где m < n, все уклонения
, где m < n, все уклонения  уклонений, входящих в каждую из этих групп, получаем систему, содержащую столько уравнений, сколько имеется неизвестных коэффициентов
уклонений, входящих в каждую из этих групп, получаем систему, содержащую столько уравнений, сколько имеется неизвестных коэффициентов  . Заметим, что поскольку сумма
. Заметим, что поскольку сумма  уклонений для каждой группы равна нулю, то равна нулю также и сумма Е всех уклонений, т.е. для нашей системы равенство (8) будет выполнено.
уклонений для каждой группы равна нулю, то равна нулю также и сумма Е всех уклонений, т.е. для нашей системы равенство (8) будет выполнено. (9)
(9)
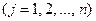 - уклонения эмпирической формулы (9) от исходных данных (
- уклонения эмпирической формулы (9) от исходных данных (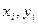 ).
). считаются те, для которых сумма квадратов уклонений
считаются те, для которых сумма квадратов уклонений

 (10)
(10) линейная относительно параметров
линейная относительно параметров  ,
,
 (11)
(11) и
и  , систему (5) можно записать в виде нормальной системы
, систему (5) можно записать в виде нормальной системы (11’)
(11’) то:
то: и
и 

 мала, то сами эти уклонения также малы по абсолютной величине. Для метода средних, где составляется алгебраическая сумма уклонений, такого вывода сделать нельзя.
мала, то сами эти уклонения также малы по абсолютной величине. Для метода средних, где составляется алгебраическая сумма уклонений, такого вывода сделать нельзя.


