Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных уравненийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Способы решения систем линейных уравнений в основном разделяются на две группы: 1) точные методы, представляющие собой конечные алгоритмы для вычисления корней системы (таковы, например, правило Крамера, метод Гаусса, метод главных элементов, метод квадратных корней и др.); 2) итерационные методы, позволяющие получать корни системы с заданной точностью путем сходящихся бесконечных процессов (к числу их относятся метод итерации, метод Зейделя, метод релаксации и др.). Вследствие неизбежных округлений результаты даже точных методов являются приближенными, причем оценка погрешностей корней в общем случае затруднительна. При использовании итерационных процессов, сверх того, добавляется погрешность метода. Наиболее распространенным приемом решения систем линейных уравнений является метод последовательного исключения неизвестных; носящий название метода Гаусса. Для простоты рассуждений ограничимся рассмотрением системы четырех уравнений с четырьмя неизвестными
Пусть
где
Пользуясь уравнением (13), легко исключить из системы (12) неизвестную
где коэффициенты
Разделив, далее, коэффициенты первого уравнения системы (12') на “ведущий элемент“
где
Исключая теперь
где
Разделив коэффициенты первого уравнения системы (12'') на ''ведущий элемент''
где
Исключив теперь
где
Отсюда
Остальные неизвестные последовательно определяются из уравнений (13''), (13') и (13):
Таким образом, процесс решения линейной системы по методу Гаусса сводится к построению эквивалентной системы (13), (13'), (13''), (13'''), имеющей треугольную матрицу. Необходимым и достаточным условием применимости метода является неравенство нулю всех ”ведущих элементов”. Вычисления удобно поместить в таблицу (табл. 2.). Схему метода Гаусса называют также схемой единственного деления. Процесс нахождения коэффициентов
При обратном ходе используются лишь строки разделов А, содержащие единицы (отмеченные строки), начиная с последней. Элемент Таблица 2.
Для контроля вычислений используют так называемые “контрольные суммы“
помещенные в столбце Если принять за новые свободные члены в системе (12), то преобразованная линейная система
будет иметь неизвестные
В самом деле, подставляя формулы (16) в уравнение (15), в силу системы (12) и формул (14) получим тождество
Вообще, если над контрольными суммами в каждой строке проделывать те же операции, что и над остальными элементами этой строки, то при отсутствии ошибок в вычислениях элементы столбца При решении систем уравнений и неравенств используется итерационный метод Левенберга – Маркардта, содержащийся в известном и свободно распространяемом пакете алгоритмов численных методов MINPACK. Этот метод пытается найти нули или минимум среднеквадратичной погрешности при решении заданной системы уравнений или системы неравенств. При решении с применением аппарата комплексных чисел раздельно решаются действительная и мнимая части уравнений.
При решении вычисляется также вектор невязки. Если его величина меньше TOL, система возвращает вектор переменных-неизвестных. Если для решения используется функция find, при величине вектора невязки больше TOL система сообщает, что решение не найдено. Когда используется функция minerr, вектор неизвестных возвращается даже в том случае, когда значение вектора невязки больше TOL. Наконец, если не обнаружено схождение за заданное число итераций, выдается сообщение об отсутствии сходимости (как при применении функции find, так и minerr). В любых случаях величина вектора невязки определяется значением переменной ERR. Для вычисления определителей матрицы и ее инвертирования используется LU-разложение. При этом матрица М разлагается в произведение нижней треугольной матрицы L и верхней U (т. е. M=L-U ). Такой метод хорошо известен. В частности, он позволяет: • вычислить определитель исходной матрицы как произведение диагональных элементов матриц L и U; • вычислить обратную матрицу из решения матричного уравнения Для решения системы уравнений напечатайте слово Given. Потом напечатайте уравнения или неравенства ниже этого слова. Напечатайте функцию Find, вводящую неизвестные величины как аргументы. Нажмите Ctrl +. Mathcad отобразит стрелку вправо. Щелкните мышкой вне функции Find. Mathcad размещает результаты в вектор. Результаты находятся в том же самом порядке как переменные функции Find. Этот пример можно использовать, для решения системы уравнений. Найти пересечение двух плоских линий: Given
Используйте [ Ctrl ] =, чтобы напечатать полужирные знаки “ = ”.
Система имеет одно решение.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.107.68 (0.012 с.) |


 (12)
(12) (ведущий элемент). Разделив коэффициенты первого уравнения системы (12) на
(ведущий элемент). Разделив коэффициенты первого уравнения системы (12) на 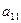 , получим:
, получим: (13)
(13)
 . Для этого достаточно из второго уравнения системы (12) вычесть уравнение (13), умноженное на
. Для этого достаточно из второго уравнения системы (12) вычесть уравнение (13), умноженное на 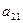 из третьего уравнения системы (12) вычесть уравнение (13), умноженное на
из третьего уравнения системы (12) вычесть уравнение (13), умноженное на 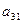 , и т.д. В результате получим систему из трех уравнений
, и т.д. В результате получим систему из трех уравнений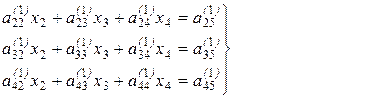 (12')
(12') вычисляются по формуле
вычисляются по формуле
 , получим уравнение
, получим уравнение (13')
(13')
 таким же способом, каким мы исключили
таким же способом, каким мы исключили 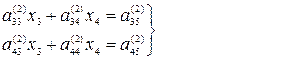 (12'')
(12'')
 , получим:
, получим: (13'')
(13'')
 аналогичным путем из системы (12''), будем иметь:
аналогичным путем из системы (12''), будем иметь: (12''')
(12''')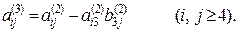
 (13''')
(13''')
 треугольной системы обычно называется прямым ходом, процесс получения значений неизвестных - обратным ходом.
треугольной системы обычно называется прямым ходом, процесс получения значений неизвестных - обратным ходом. из раздела, стоящий в столбце свободных членов отмеченной строки раздела, дает значение
из раздела, стоящий в столбце свободных членов отмеченной строки раздела, дает значение  . Далее, все остальные неизвестные
. Далее, все остальные неизвестные  шаг за шагом находятся с помощью вычитания из свободного члена отмеченной строки суммы произведений ее коэффициентов на соответствующие значения ранее найденных неизвестных. Значения неизвестных последовательно выписываются в последний раздел B. Расставленные там единицы помогают находить для
шаг за шагом находятся с помощью вычитания из свободного члена отмеченной строки суммы произведений ее коэффициентов на соответствующие значения ранее найденных неизвестных. Значения неизвестных последовательно выписываются в последний раздел B. Расставленные там единицы помогают находить для 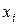 соответствующие коэффициенты в отмеченных строках.
соответствующие коэффициенты в отмеченных строках.
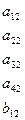


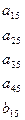








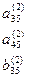

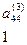
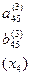







 , (14)
, (14) и представляющие собой сумму элементов строк матрицы исходной системы (12), включая свободные члены.
и представляющие собой сумму элементов строк матрицы исходной системы (12), включая свободные члены. (15)
(15)
 , связанные с прежними неизвестными
, связанные с прежними неизвестными  , соотношениями
, соотношениями (16)
(16)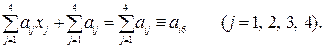
 равны суммам элементов соответствующих преобразованных строк. Это обстоятельство служит контролем прямого хода. Обратный ход контролируется нахождением чисел
равны суммам элементов соответствующих преобразованных строк. Это обстоятельство служит контролем прямого хода. Обратный ход контролируется нахождением чисел 
 .
. , где е – вектор с единицей на j -м месте и нулями в остальных позициях, V – вектор решения, который образует столбцы обратной матрицы для каждого j.
, где е – вектор с единицей на j -м месте и нулями в остальных позициях, V – вектор решения, который образует столбцы обратной матрицы для каждого j.