
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Ньютона (правило трех восьмых):Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
где
Остаточный член имеет вид
Заметим, что в формуле Ньютона число узлов обязательно равно
Рис. 4.
Если функция
где под Система MathCad вычисляет определенные интегралы методом Ромберга. Не описывая его подробно, отметим лишь, что он является вариантом метода трапеций с делением на два интервала интегрирования с итерационным уточнением решения до достижения заданной точности (она определяется значением системной переменной TOL). Если за заданное число итераций точность не достигнута, используется более точный метод Ромберга с открытыми концами. При нем число интервалов утраивается на каждом шаге интегрирования. Этот метод увеличивает число шагов интегрирования там, где подынтегральная функция меняется более резко (например, если она имеет разрыв). К достоинствам метода можно отнести то, что он делает все возможное, чтобы вычислить интеграл даже сложной функции. Но для простых функций это ведет к увеличению времени вычислений. При наличии у подынтегральной функции особенностей время вычисления может резко возрастать из-за перехода от одной реализации метода Ромберга к другой. Поэтому нередко бывает оправданным применение достаточно точных формул интегрирования, например формул Ньютона-Котесса с легко предсказуемыми узлами, которые можно выбрать вдали от особых точек подынтегральной функции. Для вычисления определенных интегралов в Mathcad нажмите & или вставьте знак интегрирования с соответствующей панели. Функция Подобно всем численным методам, алгоритм интегрирования Mathcad может иметь трудности с неправильными подынтегральными выражениями. Если подынтегральное выражение имеет особенности, разрывы, или большую и быструю флуктуацию, решение Mathcad может быть неточно. Чтобы вычислить двойные или кратные интегралы, нажмите & несколько раз. В следующем примере вычисляется определенный интеграл действительной функции f(x,y) в некоторой плоской области. Вводятся границы области интегрирования, принимаются а < x < b и с(x)<y<d(x) для всех x:
Вводится подынтегральная функция, описывающая плотность треугольника:
Тогда его масса вычисляется следующим образом:
3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ Задача Коши для дифференциального уравнения n- го порядка
заключается в отыскании функции
где Найти общее решение задачи Коши удается в редких случаях, поэтому чаще всего приходится решать задачу Коши приближенно. Приближенные методы в зависимости от формы, в которой они представляют решение, можно разделить на две группы. 1) Аналитические методы, дающие приближенное решение дифференциального уравнения в виде аналитического выражения. 2) Численные методы, дающие приближенное решение в виде таблицы. В дальнейшем изложении предполагается, что для рассматриваемых уравнений выполнены условия существования и единственности решения. К наиболее часто используемым численным методам решения дифференциальных уравнений относятся методы Эйлера и Рунге-Кутта, имеющие, в свою очередь, несколько модификаций. Метод Эйлера относится к численным методам, дающим решение в виде таблицы приближенных значений искомой функции y(x). Пусть дано дифференциальное уравнение
с начальным условием Выбрав достаточно малый шаг h, рассмотрим систему равноотстоящих точек В методе Эйлера приближенные значения
При этом искомая интегральная кривая Если правая часть уравнения (1) в некотором прямоугольнике
то имеет место следующая оценка погрешности:
где Формула (3) имеет лишь теоретическое применение. На практике иногда оказывается более удобным двойной просчет: расчет повторяют с шагом Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка. Рассмотрим систему двух уравнений первого порядка
с начальными условиями
Рис. 5.
Приближенные значения
Существует несколько модификаций метода Эйлера. Первый улучшенный метод Эйлера для решения задачи (1), (2) состоит в том, что сначала вычисляют промежуточные значения, а затем полагают
Второй улучшенный метод – метод Эйлера–Коши -заключается в том, что сначала определяют "грубое приближение"
затем вычисляют
Оценка погрешности в точке
где Метод Эйлера-Коши решения задачи (1), (2) можно ещё более уточнить, применяя итерационную обработку каждого значения y1 (метод Эйлера с последующей итерационной обработкой). Исходя из грубого приближения
рассмотрим итерационный процесс
Итерации продолжаем до тех пор, пока в двух последовательных приближениях
Как правило, при достаточно малом h итерации быстро сходятся. Если после трёх–четырёх итераций не произошло совпадения нужного числа десятичных знаков, то следует уменьшить шаг расчета h. Блок-схемы модифицированных методов Эйлера легко получить самостоятельно, по аналогии с рис. 5. При решении методом Рунге-Кутта дифференциального уравнения (1) с начальными условиями (2) через
где
Схема метода Рунге-Кутта приведена в таблице 1. Таблица 1.
Порядок заполнения таблицы (выполнения вычислений по методу Рунге-Кутта): 1. Выбираются x и y. 2. Вычисляются 3. Определяются 4. Вычисляются 5. Принимаются 6. Вычисляются 7. Определяются 8. Вычисляются 9. Суммируются 10. Вычисляются Затем все вычисления продолжаются в том же порядке, принимая за начальную точку Заметим, что шаг расчета можно менять при переходе от одной точки к другой. Для контроля правильности выбора шага h рекомендуется вычислять дробь
Величина Метод Рунге-Кутта имеет порядок точности
где При реализации на ЭВМ метода Рунге-Кутта на ЭВМ с автоматическим выбором шага обычно в каждой точке Блок-схему решения обыкновенного дифференциального уравнения методом Рунге-кутта с автоматическим выбором шага можно получить самостоятельно.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.36.89 (0.011 с.) |

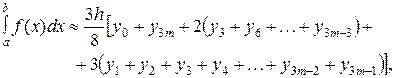
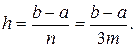
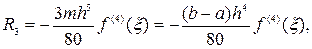
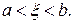
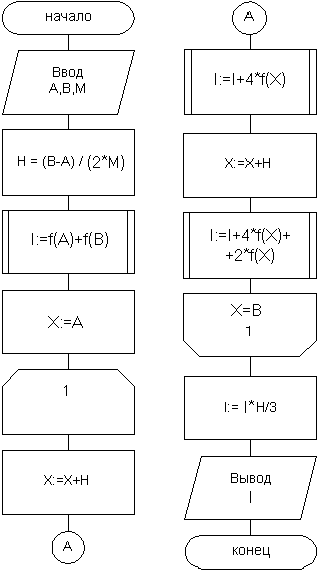
 , т.е.
, т.е. 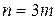 .
.
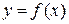 задана таблично, а ее производные найти затруднительно, то в предположении отсутствия быстро колеблющихся составляющих можно применять приближенные формулы для погрешностей, выраженные через конечные разности:
задана таблично, а ее производные найти затруднительно, то в предположении отсутствия быстро колеблющихся составляющих можно применять приближенные формулы для погрешностей, выраженные через конечные разности: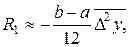
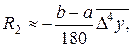

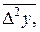
 подразумевается арифметическое среднее значение разностей соответствующего порядка.
подразумевается арифметическое среднее значение разностей соответствующего порядка.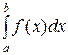 возвращает определенный интеграл f(x) от а до b, где F – любая скалярная функция, определенная в замкнутом интервале [a, b]; x – аргумент этой скалярной функции. а и b должны быть действительными скалярными величинами, но f(х) может быть комплексной величиной. а и b должны иметь одинаковые размерности, если они есть.
возвращает определенный интеграл f(x) от а до b, где F – любая скалярная функция, определенная в замкнутом интервале [a, b]; x – аргумент этой скалярной функции. а и b должны быть действительными скалярными величинами, но f(х) может быть комплексной величиной. а и b должны иметь одинаковые размерности, если они есть.  может быть функцией любого числа переменных.
может быть функцией любого числа переменных.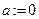

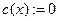

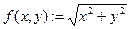
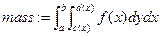
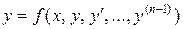 ,
,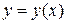 удовлетворяющей этому уравнению и начальным условиям:
удовлетворяющей этому уравнению и начальным условиям:
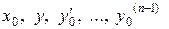 - заданные числа.
- заданные числа.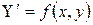 (1)
(1)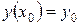 . (2)
. (2)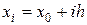
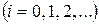
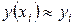 вычисляются последовательно по формулам
вычисляются последовательно по формулам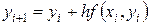
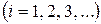 .
. , проходящая через точку
, проходящая через точку  , заменяется ломаной
, заменяется ломаной  с вершинами
с вершинами 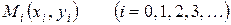 ; каждое звено
; каждое звено 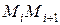 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (1), которая проходит через точку
этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (1), которая проходит через точку 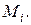
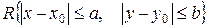 удовлетворяет условиям
удовлетворяет условиям
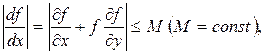 (3)
(3)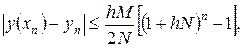
 - значение точного решения уравнения при
- значение точного решения уравнения при  а
а 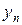 - приближенное значение, полученное на n- м шаге.
- приближенное значение, полученное на n- м шаге.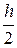 и погрешность более точного значения
и погрешность более точного значения 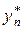 (при шаге
(при шаге 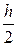 ) оценивают приближенно так:
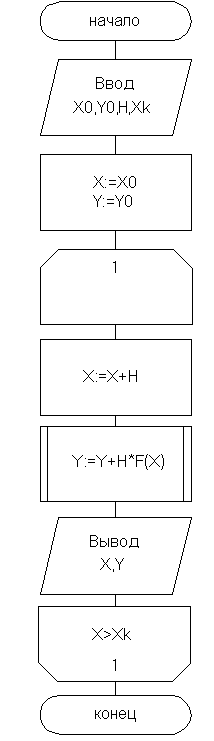
) оценивают приближенно так:  . Блок-схема алгоритма решения дифференциального уравнения методом Эйлера приведена на рис. 5.
. Блок-схема алгоритма решения дифференциального уравнения методом Эйлера приведена на рис. 5.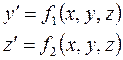

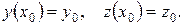
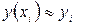 и
и 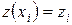 вычисляются последовательно по формулам
вычисляются последовательно по формулам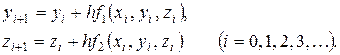
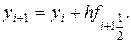
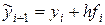
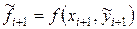 и приближенно полагают
и приближенно полагают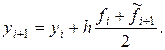
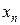 может быть получена с помощью двойного просчета: расчет повторяют с шагом
может быть получена с помощью двойного просчета: расчет повторяют с шагом 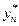 (при шаге
(при шаге 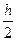 ) оценивают приближенно так:
) оценивают приближенно так: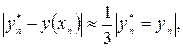
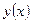 - точное решение дифференциального уравнения.
- точное решение дифференциального уравнения.
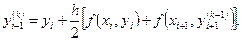
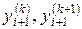 не совпадут соответствующие десятичные знаки. После этого полагаем
не совпадут соответствующие десятичные знаки. После этого полагаем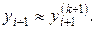
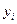 обозначают приближенное значение искомого решения в точке x1 и вычисление приближенного значения
обозначают приближенное значение искомого решения в точке x1 и вычисление приближенного значения 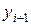 в следующей точке
в следующей точке 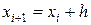 производится по формулам
производится по формулам


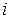

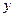
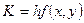

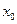
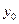

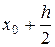
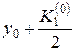
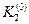
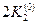
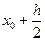

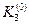
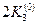
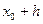
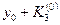

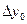
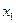

 . Определяются
. Определяются 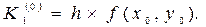
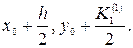
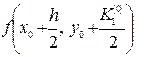 и
и  .
.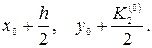
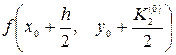

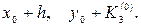
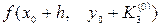 и
и 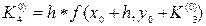 .
.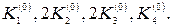 , делим на 6 и получаем таким образом
, делим на 6 и получаем таким образом 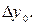
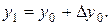
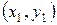 .
.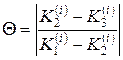 .
. не должна превышать нескольких сотых. В противном случае шаг h следует уменьшить.
не должна превышать нескольких сотых. В противном случае шаг h следует уменьшить.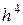 на всем отрезке
на всем отрезке 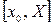 .Оценка погрешности метода очень затруднительна. Грубую оценку погрешности можно получить с помощью двойного просчета по формуле
.Оценка погрешности метода очень затруднительна. Грубую оценку погрешности можно получить с помощью двойного просчета по формуле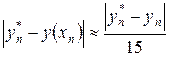 ,
,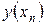 - значение точного решения уравнения в точке
- значение точного решения уравнения в точке  а
а 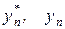 - приближенные значения, полученные с шагом
- приближенные значения, полученные с шагом 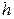 .
.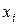 делают двойной просчет - сначала с шагом h, затем с шагом
делают двойной просчет - сначала с шагом h, затем с шагом 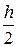 .Если полученные при этом значения
.Если полученные при этом значения 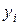 различаются в пределах допустимой точности, то шаг
различаются в пределах допустимой точности, то шаг  для следующей точки
для следующей точки  удваивают, в противном случае берут половинный шаг.
удваивают, в противном случае берут половинный шаг.


