
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование последовательностей и рядовСодержание книги
Поиск на нашем сайте
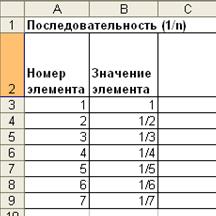
Создание массива элементов числовой последовательности При решении некоторых задач необходимо использовать последовательности. Различают два вида последовательностей - числовые и функциональные. Числовые последовательности представляют собой множества чисел. Если каждому числу n из натурального ряда чисел 1,2,3,..., п поставлено в соответствие вещественное число xn то множество чисел x1, x2, x3…, xn называют числовой последовательностью. Числа x1, x2, x3…, xn называют членами последовательности, элемент хп - общим элементом, а число п - его номером. Таким образом, числовая последовательность представляет собой множество пронумерованных элементов. Говорят, что последовательность задана, если известен способ получения любого ее элемента. Последовательность обозначается символом {хn}. Например, символ {1/n} - обозначает последовательность чисел 1, В общем случае для создания массива элементов последовательности в табличном процессоре нужно выполнить следующие действия: —создать массив, содержащий множество чисел натурального ряда. Каждый элемент этого массива является номером элемента создаваемой числовой последовательности; —ввести в ячейку формулу последовательности, делая в ней адресные ссылки на ячейки, содержащие номера элементов последовательности; —скопировать введенную формулу во все другие ячейки диапазона, в котором формируется числовая последовательность. Для иллюстрации приведенной технологии на рис. 1.13а приведен пример создания последовательности {1/n}, а на рис. 1.136 - последовательности {n/(n+1)} для семи элементов.
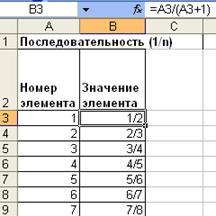
а) б) Рис. 1.13 Примеры создания числовых последовательностей: а){1/n};б){n/(n+1)}
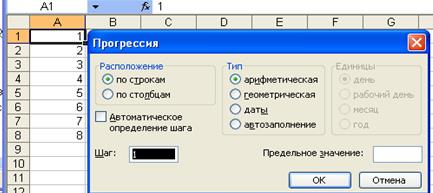
Для создания наиболее часто встречающихся последовательностей, таких как арифметическая или геометрическая прогрессия, табличный процессор имеет специальный инструмент Прогрессия, который включается командой меню Правка/Заполнить/Прогрессия. Для создания последовательности с помощью этого инструмента нужно: —ввести значение первого элемента прогрессии в ячейку рабочего листа; —выделить диапазон ячеек для членов прогрессии; —выполнить команду меню Правка/Заполнить/Прогрессия; —в появившемся окне диалога Прогрессия указать тип и параметры создаваемой последовательности (рис. 1.14).
Рис. 1.14 Диалоговое окно прогрессия Приближенное вычисление пределов числовых последовательностей Технологию приближенного вычисления предела числовой последовательности рассмотрим на примере. Пример 1.12 Найти предел числовой последовательности Решение Пологая, что в ячейке А2 будет находиться число n, в ячейку рабочего листа В2 введем формулу =А2/(А2+1). В ячейку А2 введем большое число, примерно равное 1
Рис. 1.15
Применение последовательностей в экономических моделях Рассмотрим примеры практического применения пределов числовых последовательностей в экономике и финансах. Известно, что формула сложных процентов имеет вид
где Q0- первоначальная сумма вклада в банк; р - процент начисления за определенный период времени; k - количество периодов времени хранения вклада; Qk - сумма вклада по истечении k периодов. Если полагать, что проценты начисляются непрерывно, то справедлива формула
Пример 1.13 Пусть начальный вклад равен 1000 денежных единиц, процентная ставка составляет 10% годовых, начисление процентов непрерывное. Требуется определить, какая сумма вклада будет по истечении двух лет при условии, что финансовый год равен 360 дням. Решение Ставка за весь период составит m=10% Введем исходные данные на рабочий лист, как показано на рисунке, и число n – достаточно большое. В ячейку Е2 введем формулу для вычисления суммы вклада по истечении двух лет =$D$2*((1+1:$A$2)^$A$2)^E2 (рис.1.16).
Рис. 1.16
Результат вычисления приведен на рисунке – Qk=1221,40278 руб. (рис.1.17).
Рис. 1.17
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.245.203 (0.008 с.) |

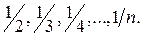
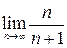 .
.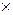 1012, но не более высокого порядка (в противном случае может наступить переполнение разрядной сетки процессора ПК и результат получится неправильным). После ввода числа в ячейку В2 отобразится приближенное значение предела числовой последовательности (рис.1.15).
1012, но не более высокого порядка (в противном случае может наступить переполнение разрядной сетки процессора ПК и результат получится неправильным). После ввода числа в ячейку В2 отобразится приближенное значение предела числовой последовательности (рис.1.15).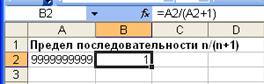

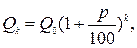
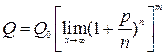 , где m-kp/100 – процентная ставка, вычисленная за весь расчетный период и выраженная десятичной дробью.
, где m-kp/100 – процентная ставка, вычисленная за весь расчетный период и выраженная десятичной дробью.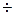 100=0,2.
100=0,2.




