Технология получения математической модели функции по ее табличному представлению

На практике часто бывает необходимо получить аналитическую формулу для функциональной зависимости, полученной экспериментально, модель которой представлена в виде таблицы. Это бывает необходимо в тех случаях, когда нужно найти значение функции в тех точках внутри данного интервала, где она таблично не задана - задача Интерполяции, либо вычислить значение функции в точках за пределамизаданного интервала - задача экстраполяции.

Решение задач интерполяции и экстраполяции обеспечивается построением интерполяционной или аппроксимирующей функции L(x), приближенно заменяющей исходную f(x), заданную таблично. Подбор аналитической формулы сводится к вычислению входящих в нее параметров таким образом, чтобы из всех функций такого вида выбрать ту, которая наилучшим образом описывает зависимость между изучаемыми величинами.

При построении аппроксимирующей функции должны быть решены следующие вопросы:

- выбор типа аппроксимирующей функции L(x);

- оценка погрешности аппроксимации.

Подбираемая эмпирическая функция в зависимости от характерны экспериментальных данных может быть следующих видов:

- линейная (у = ах + b) обычно применяется в тех случаях, когда экспериментальные данные изменяются относительно постоянно;

- полиноминальная (у = а₀ + а₁х +а₂ х²+...+ a_n хⁿ) - используется для описания экспериментальных данных, попеременно возрастающих и убывающих;

- логарифмическая (у = а lпх + b), где а и b - константы, - применяется для описания экспериментальных данных, которые первоначально быстро возрастают или убывают, а затем постепенно стабилизируются;

- степенная (у = bx^-a), где a u b - константы, - используется для аппроксимации экспериментальных данных, скорость изменения которых увеличивается или уменьшается;

- экспоненциальная (y=be^ax), где а и b - константы, - применяется экспериментальных данных, которые быстро возрастают или убывают, а затем стабилизируются.

Близость исходной и аппроксимирующей функций определяется критерием аппроксимации. Наиболее распространен квадратичный критерий (R²), именно такой критерий оценки применяется в табличном процессоре. Не вдаваясь в подробности вычисления этого критерия, скажем: чем ближе значение этого критерия к единице, тем ближе аппроксимирующая функция к исходной, тем точнее полученная аналитическая модель отражает функциональную зависимость.

Чтобы получить аппроксимирующую формулу в табличном процессоре, нужно выполнить следующую последовательность действий:

- построить по имеющейся таблице экспериментальных данных графическую модель функции;

- установить указатель мыши на линию графика (ряд) и вызвать контекстное меню;

- в контекстном меню выбрать Добавить линию тренда - откроется диалоговое окно Линия тренда;

- в диалоговом окне Линия тренда на вкладке Тип, учитывая характер изменения функции на графике, выбрать вид аппроксимирующей функции, а на вкладке Параметры задать дополнительные параметры, в том числе установить флажок Показывать уравнение на диаграмме.

После выполнения приведенных операций на диаграмме будет отображена линия тренда (графическое отображение аппроксимирующей функции), а также аппроксимирующая функция в аналитическом виде.

Рассмотрим процесс получения аппроксимирующей функции на примере.

Пример 1.21 Имеются сведения о величинах страховых выплат по годам, представленные в таблице. Требуется исследовать характер изменения величины страховых выплат и подобрать аппроксимирующую функцию (таблица 1.6.).

Таблица 1.6

Год	Сумма страховых выплат (руб.)
	150 000
	200 000
	300 000
	450 000
	450 000
	420 000

Решение

В ячейки рабочего листа введем исходные данные в виде таблицы (рис. 1.27).

Рис. 1.27

 

По данным таблицы, полученным экспериментально, построим график. На графике видно, что экспериментальные данные вначале растут, а затем убывают и есть только один экстремум. Следовательно, в качестве аппроксимирующей функции следует выбрать полиноминальную функцию третьей степени (рис. 1.28).

Рис. 1.28

 

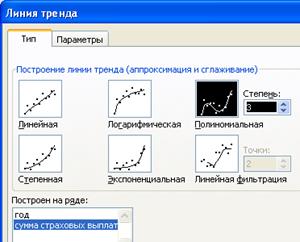
Откроем контекстное меню и выберем пункт Добавить линию тренда.

В диалоговом окне Линия тренда на вкладке Тип выберем Полиномиальная и установим Степень, равную трем. На вкладке Параметры установим флажки Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации R².

После щелчка на кнопке ОК на диаграмме отобразится линия тренда и аналитическая запись аппроксимирующей функции

y = - 9259,3x³ + 6E + 07x² – 1E + 11x + 7E + 13, R² = 0,9818 (рис.1.29)

 

Рис. 1.29

 

Величина R² близка к единице, следовательно, степень достоверности аппроксимации является высокой.