
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полученные результаты и их интерпретацияСодержание книги
Поиск на нашем сайте
- Коэффициент детерминации R-квадрат =0,974641 (аппроксимация высокая). - Значимость F= 0,000643 (р < 0,05 - регрессионная модель значима). - Y- пересечение а0= 2102438,6. - а1, = 6,4004 - коэффициент при независимой переменной Затраты на рекламу по телевидению. - а2 = -54,068 - коэффициент при независимой переменной Затраты на рекламу в метро. С учетом полученных данных функциональная зависимость величины прибыли от затрат на рекламу запишется в виде полинома у = 2102438,6 + 6,4004% - 54,068х2; x1 – величина затрат на рекламу по телевидению; х2 - величина затрат на рекламу в метро. Используя полученное уравнение регрессии, можно решить задачу оптимизации прибыли или спрогнозировать ожидаемую прибыль при другом распределении средств на рекламу. Пример 2.17 Организация может истратить на рекламу по телевидению и на рекламу в метро 170 000 руб. Требуется оптимальным образом распределить затраты на различные виды рекламы с целью получения максимальной прибыли. Решение. Математическая модель В качестве целевой функции возьмем уравнение регрессии, полученное в примере 2.16: у=2102438,6 + 6,4004х1, - 54,068х2 => max. Ограничения: х1 + х2 <= 170 000, х1 >= 0, х2 >= 0. Используя инструмент Поиск решения, решим задачу. Модель и результат решения приведены на рис. 2.26.
Рис. 2.26 Задания для практической работы Задание 2.1 1.Создайте массив из 100 чисел, распределенных равномерно на интервале 1-100. 2.Создайте массив из 100 чисел, распределенных нормально с математическим ожиданием 50, стандартное отклонение - 10, случайное рассеивание - 2. 3.Создайте массив случайных чисел, распределенный по биноминальному закону для параметров: количество испытаний N = 10, вероятность благоприятного исхода одного испытания Р = 0,3. Задание 2.2 1. Вычислите математическое ожидание и стандартное отклонение дискретного распределения 0,2; 0,5; 2; 3; 5,1; 8; 2; 3. 2. Найдите 25%-ную квартиль для дискретного распределения 0,2; 15; 2; 3; 5,1; 8; 2; 3. 3. Вычислите дисперсию для дискретного распределения 0,2; 0,5; 13; 5,1; 8; 2; 3. Задание 2.3 1. Ежедневные расходы на обслуживание и рекламу автомобилей в автосалоне составляют в среднем 120 тыс. ден. ед., а число продаж X автомобилей подчиняется закону распределения.
Вычислите математическое ожидание ежедневной прибыли при цене автомобиля 150 тыс. ден. ед.
2. Найти дисперсию и среднее квадратичное отклонение случайной величины X, заданной законом распределения
Задание 2.4 Книга издана тиражом 100 тыс. экземпляров. Вероятность брака в экземпляре равна 0,0001. Требуется найти вероятность того, что тираж содержит 5 бракованных книг. Задание 2.5 1. Постройте диаграмму стандартного нормального интегрального распределения (стандартное нормальное распределение имеет М = 0 и 2. Вычислите верхний и нижний квартили для нормальной функции плотности вероятности f(х) при М = 24,3 и 3. Вычислите вероятность того, что появится случайная величина х 4. Вычислите квантиль для р = 0,908789 нормального распределения с М = 20, 5. Магазин продает мужские костюмы. Распределение спроса по размерам является нормальным с математическим ожиданием М = 48 и
Задание 2.6 По данным, приведенным в таблицах, постройте эмпирическую функцию распределения роста.
Задание 2.7 Определите, лежит ли значение 19 внутри 95%-го доверительного интервала выборки 2, 3, 5, 7, 4, 9, 6, 4, 9, 10, 4, 7, 19. Задание 2.8. Найдите распределение по абсолютным частотам для следующих результатов тестирования в баллах: 79,85, 78,85,83, 81,95, 88, 97 для интервалов с границами: 70, 79, 89. Задание 2.9 Определите, имеется ли взаимосвязь и какая между годовым уровнем инфляции, ставкой рефинансирования и курсом валюты по следующим данным ежегодных наблюдений.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какими способами можно получить массив случайных чисел, распределенных по стандартному нормальному закону? 2.Что называется законом распределения случайной величины? 3.Что такое дискретное равномерное распределение? 4.Укажите виды распределений при генерации случайных чисел? 5.Что является первым моментом случайной величины? 6.Что является вторым моментом, характеризующим разброс случайной величины относительно математического ожидания? 7. Какими способами можно получить массив случайных чисел, распределенных по нормальному закону, отличающегося от стандартного?
8.Что такое квантиль? 9.Что называется медианой? 10.Как вычисляется математическое ожидание при распределении, заданном таблично? 11.Как вычисляется дисперсия дискретной случайной величины? 12.Как вычисляется среднеквадратичное отклонение дискретной случайной величины? 13. Поясните технологии вычисления математического ожидания, дисперсии стандартного отклонения? 14.Что такое биноминальное распределение? 15. Какие функции табличного процессора предназначены для вычисления числовых характеристик биноминального распределения? 16.Для чего служит функция НОРМОБР? 17.Для чего предназначена функция НОРМСТОБР? 18.Что вычисляет функция НОРМАЛИЗАЦИЯ? 19. В чем заключается суть численных методов построения выборочной функции распределения? 20.Что такое выборочная совокупность? 21.Что вычисляет функция ЧАСТОТА? 22.для чего служит инструмент Гистограмма? 23. Поясните содержание технологии проверки статистической гипотезы. 24.Перечислите функции, характеризующие центр распределения выборочных характеристик. 25.Перечислите функции, характеризующие рассеивание выборочных характеристик. 26.Перечислите функции, позволяющие оценить форму эмпирического распределения выборочных характеристик. 27.Что позволяет вычислить инструмент Описательная статистика? 28. Какими способами можно вычислить доверительный интервал для среднего? 29.Укажите назначение и параметры функции ХИ2ТЕСТ. 30. Какие инструменты служат для решения задач дисперсионного и корреляционного анализа? 31.В чем отличие однофакторного дисперсионного анализа от двуфакторного? 32. Что такое корреляция? 33.Что называется коэффициентом корреляции? 34.Что представляет собой корреляционная матрица? 35.Поясните содержание технологии регрессионного анализа. 36.Что такое критерий Фишера? 37.Что такое аппроксимация?
Практическая работа №3
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.25.115 (0.012 с.) |




 = 1). Используйте функцию НОРМСТРАСП.
= 1). Используйте функцию НОРМСТРАСП.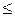 42 при нормальном законе распределения вероятностей с М = 40 и
42 при нормальном законе распределения вероятностей с М = 40 и 




