
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задач линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель: изучить технологию решения задач линейного программирования средствами Excel.
Теоретическое введение Большую часть задач оптимизации представляют собой задачи линейного программирования, т. е. такие, у которых критерий оптимизации и ограничения – линейные функции. В этом случае для решения задачи следует установить флажок Линейная модель в окне Параметры поиска решения. Это обеспечит применение симплекс-метода. В противном случае даже для решения линейной задачи будут использоваться более общие (т. е. более медленные) методы. Поиск решения может работать также и с нелинейными зависимостями и ограничениями. Это, как правило, задачи нелинейного программирования или, например, решение системы нелинейных уравнений. Для успешной работы средства Поиск решения следует стремиться к тому, чтобы зависимости были гладкими или, по крайней мере, непрерывными. Наиболее часто разрывные зависимости возникают при использовании функции если то, среди аргументов которой имеются переменные величины модели. Проблемы могут возникнуть также и при использовании в модели функций типа ABS(), ОКРУГЛ() и т. д. Решая задачи с нелинейными зависимостями, следует: ввести предварительно предположительные значения искомых переменных (иногда легко получить графическое представление решения и сделать приблизительные выводы о решении); в окне Параметры поиска решения снять (если установлен) флажок. При необходимости проводится анализ решения. Часто добавляют также представление решения в виде графиков или диаграмм. Можно получить и отчет о поиске решения. Отчеты бывают трех типов: Результаты, Устойчивость, Пределы. Тип отчета выбирается по окончании поиска решения в окне Результаты поиска решения в списке Тип отчета (можно выбрать сразу два или три типа). Отчет типа Результаты содержит окончательные значения параметров задачи целевой функции и ограничений. Отчет типа Устойчивость показывает результаты малых изменений параметров поиска решения. Отчет типа Пределы показывает изменения решения при поочередной максимизации и минимизации каждой переменной при неизменных других переменных.
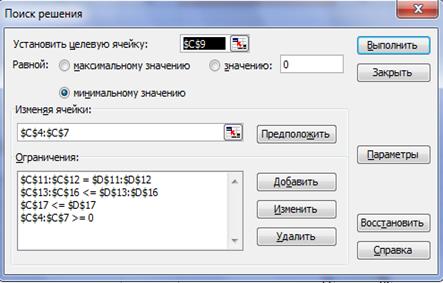
Технология решения задачи линейного программирования Пример 1. Двум погрузчикам разной мощности не более чем за 24 ч нужно погрузить на первой площадке 230 т, на второй – 168 т. Первый погрузчик на первой площадке может погрузить 10 т в час, на второй – 12 т в час. Второй погрузчик на каждой площадке может погрузить по 13 т в час. Стоимость работ, связанных с погрузкой 1 т первым погрузчиком на первой площадке – 8 у. е., на второй – 7 у. е.; вторым погрузчиком на первой площадке – 12 у. е., на второй– 13 у. е. Нужно составить план работы, т. е. найти, какой объем работ должен выполнить каждый погрузчик на каждой площадке, чтобы стоимость всех работ по погрузке была минимальной. Следует учесть, что по техническим причинам первый погрузчик на второй площадке должен работать не более 16 ч [4]. Решение. 1. Математическая модель. Пусть x 11 – объем работ, выполненный первым погрузчиком на первой площадке, т; x 12 – объем работ, выполненный первым погрузчиком на второй площадке, т; x 21 – объем работ, выполненный вторым погрузчиком на первой площадке, т; x 22 – объем работ, выполненный вторым погрузчиком на второй площадке, т. Определение функции цели: Ограничения на переменные: 2. Ввод исходных данных. Экранная форма для ввода условий задачи вместе с введенными в нее исходными данными представлена на рис. 1.1. Установка необходимых параметров задачи в окне Поиск решения представлена на рис. 1.2.
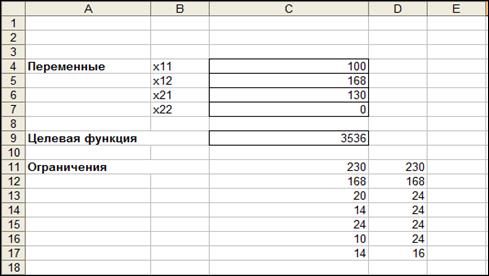
Рис. 1.1. Рабочий лист MS Excel для решения задачи
Рис. 1.2. Установка необходимых параметров задачи в окне Поиск решения
Рис. 1.3. Результат расчета надстройки Поиск решения По результатам решения задачи можно сделать вывод, что для минимизации стоимости погрузочных работ первый погрузчик на первой площадке должен погрузить 100 т, на второй – 130 т, второй погрузчик на первой площадке – 130 т; использование второго погрузчика на второй площадке в данных условиях нецелесообразно (рис. 1.3). Пример 2. Для работы в офисе автотранспортной компании требуется в понедельник - среду не менее 24 работников, в четверг и субботу – не менее 22 работников, в пятницу – не менее 20 работников, основной пик работы приходится на воскресенье, поэтому в воскресенье требуется не менее 28 сотрудников. Причем должен соблюдаться следующий рабочий график: каждый сотрудник работает 5 дней в неделю с двумя выходными подряд. Дневная оплата сотрудников составляет 400 руб. (без учета премиальных и комиссионных). Определите оптимальное количество человек в смену для обслуживания офиса автотранспортной компании с учетом минимума издержек на заработную плату, учитывая установленный график работы персонала. Решение. 1. Математическая модель. Пусть
Матрица необходимого количества сотрудников на каждый рабочий день:
Матрица почасовой оплаты труда:
Система ограничений на обязательный минимум количества сотрудников в каждый рабочий день:
Ограничение на неотрицательность переменных модели:
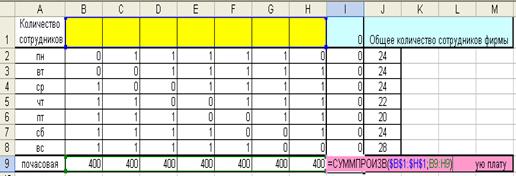
Рис. 1.4. Экранная форма задачи
При наборе графика работы персонала учитывается пять рабочих дней и два выходных в неделю. Все рабочие графики вводятся в массив (B2:H8), причем «1» означает рабочий день графика, а «0» – выходной. Так, первый график, представленный в столбце В, имеет два выходных (в понедельник и вторник) и 5 рабочих дней (со среды по воскресенье). Массив (B1:H1) соответствует переменным задачи, т.е. количеству сотрудников, работающих по определенному графику. В ячейке I2 вводится формула СУММПРОИЗВ, рассчитывающая количество сотрудников, работающих в понедельник (рис.1.5). Аналогичные формулы вводятся и в ячейках I3:I8.
Рис. 1.5. Ввод левой части ограничений
В ячейке I9 вводится целевая функция издержек фирмы на заработную плату (рис. 1.6).
Рис. 1.6. Ввод целевой функции
Для расчета общего количества сотрудников вводится формула СУММ(В1:Н1) в ячейку I1. Граничные условия и ограничения вводят аналогично предшествующей задаче с помощью диалоговых окон Добавление ограничения и Параметры поиска решения. Целевую ячейку устремляют к минимуму. Окно Поиск решения после ввода всех необходимых данных задачи представлено на рис. 1.7.
Рис. 1.7. Окно Поиск решения задачи
Рис. 1.8. Окно Параметры поиска решения задачи
В данном примере можно использовать ограничение целых чисел, если дробное число сотрудников недопустимо. Можно добавить ограничение на общее число сотрудников:
Рис. 1.9. Экранная форма задачи после получения решения
Распределение сотрудников по рабочим графикам следующее: § 6 сотрудников работают по рабочим графикам с выходными в понедельник-вторник и четверг-пятницу; § 4 сотрудника работают по графикам с выходными вторник-среда, среда-четверг и воскресенье-понедельник; § 8 сотрудников имеют график работы с выходными в пятницу-субботу; § 2 сотрудника – с выходными в субботу-воскресенье. Всего фирме требуется 34 сотрудника, еженедельные затраты на заработную плату – 13600 руб.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1956; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.216 (0.006 с.) |



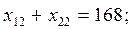
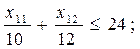

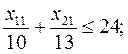



 – число сотрудников, работающих по j -му графику. Матрица графиков работы сотрудников А:
– число сотрудников, работающих по j -му графику. Матрица графиков работы сотрудников А:
 .
. .
.
 2. Ввод исходных данных. Экранная форма для ввода условий задачи вместе с введенными в нее исходными данными представлена на рис. 1.4.
2. Ввод исходных данных. Экранная форма для ввода условий задачи вместе с введенными в нее исходными данными представлена на рис. 1.4.



 , Х – максимально допустимое число сотрудников фирмы. Выбор линейной модели и неотрицательных переменных в диалоговом окне Параметры ускорит получение результата (см. рис. 1.8). Решая данную задачу, получаем рис. 1.9:
, Х – максимально допустимое число сотрудников фирмы. Выбор линейной модели и неотрицательных переменных в диалоговом окне Параметры ускорит получение результата (см. рис. 1.8). Решая данную задачу, получаем рис. 1.9:



