
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 1. Вычисление показателей вариацииСодержание книги
Поиск на нашем сайте Задача 1. Вычисление показателей вариации Вычислите показатели вариации по каждой из выборок X, Y, Z: · среднее арифметическое; · моду; · медиану; · размах вариации; · дисперсию; · стандартное отклонение; · среднее линейное отклонение; · коэффициент вариации.
Решение: Среднее значение ‑ средняя арифметическая простая: где n ‑ объем выборки.
Например, если объем исследуемой совокупности n = 20, то номер медианы
Тогда медианой будет среднее из двух значений признака, стоящих в упорядоченном ряду под номерами 10 и 11:
Размах вариации ‑ разность между максимальным и минимальным значениями признака в совокупности:
Среднее линейное отклонение: Среднее квадратическое отклонение ( Формула расчета следующая: Квадрат среднего квадратического отклонения называется дисперсией ( Она вычисляется по формуле
:
Аналогично рассчитаем показатели для выборок yи z:
Найдем среднее значение по У:
Мода по У:
Медиана по У:
Размах вариации ‑ разность между максимальным и минимальным значениями признака в совокупности:
Среднее линейное отклонение по У:
Среднее квадратическое отклонение по У:
Дисперсия по У:
Коэффициент вариации:
Расчет показателей вариации. Табл.3
Найдем среднее значение по Z:
Медиана по Z:
Размах вариации
Среднее квадратическое отклонение по Z:
Дисперсия по Z:
Среднее линейное отклонение по Z:
Коэффициент вариации:
Расчет показателей вариации. Табл.4
Задача 2. Построение ряда распределения По каждой из выборок X, Y, Z: • проведите группировку данных по интервалам равной длины; • составьте вариационный ряд; • вычислите абсолютные, относительные и накопленные частоты; постройте полигон, гистограмму и кумуляту.
Решение:
Группировка данных и построение вариационного ряда. Табл.5
Рассчитаем по у: Ход решения аналогичный расчетам по Х.
Группировка данных и построение вариационного ряда.
Табл.6
Рис.5 Полигон распределения частот по выборке Y
Рассчитаем по z:
Ход решения аналогичный расчетам по Х.
Группировка данных и построение вариационного ряда. Табл.7
Задача 3. Расчет параметров ряда распределения По сгруппированным данным и графикам определите: · среднее арифметическое; · моду; · медиану; · первую и девятую децили; · коэффициент децильной дифференциации.
Решение: Среднее значение ‑ средняя арифметическая взвешенная:
Расчет среднего значения. Табл.8
Номер медианы нам известен из Задания 1. NMe = 5,5 Точное значение медианы для сгруппированных данных рассчитываем по формуле
где xMe ‑ нижняя граница медианного интервала; h – величина медианного интервала; SMe –1 ‑ накопленная частота (частость) предмедианного интервала, fMe ‑ частота (частость) медианного интервала.
Первая и девятая децили находятся по формулам:
Коэффициент децильной дифференциации находится по формуле (KD):
Рассчитаем по У:
Ход решения аналогичен, как при расчетах по Х.
Расчет среднего значения. Табл.9
Найдем медиану для у:
Найдем первую и девятую децили по у:
Коэффициент децильной дифференциации
Рассчитаем по Z:
Ход решения аналогичен, как при расчетах по Х.
Расчет среднего значения. Табл.10
Значение моды по сгруппированным данным также можно определить по формуле
Найдем медиану для z:
Найдем первую и девятую децили по z:
Коэффициент децильной дифференциации
Задача 6. Построение уравнения регрессии Постройте уравнения регрессии Y(X), Z(X), Z(X) графическим способом. Y(X): Решение: Линия регрессии представлена на графиках в Задании 5. На линии регрессии выбираем две точки, ближе к краям диапазона значений. Уравнение регрессии имеет вид
Составляем систему уравнений ‑ два уравнения с двумя неизвестными:
Уравнение регрессии
Z(X):
Уравнение регрессии
Z(Y):
Уравнение регрессии
Корреляции
Вычислите линейные коэффициенты корреляции Решение:
Вычислим коэффициент rxy:
Вычислим коэффициент rxz:
Вычислим коэффициент ryz:
При
Корреляции После определения коэффициентов корреляции Решение:
Величина t -критерия имеет вид
где r – выборочный коэффициент корреляции; n – объем выборки.
Проверим существенность коэффициента корреляции rxy:
0,408<2,306, значит гипотеза
11,28>2,306, значит гипотеза
Задача 1. Вычисление показателей вариации Вычислите показатели вариации по каждой из выборок X, Y, Z: · среднее арифметическое; · моду; · медиану; · размах вариации; · дисперсию; · стандартное отклонение; · среднее линейное отклонение; · коэффициент вариации.
Решение: Среднее значение ‑ средняя арифметическая простая: где n ‑ объем выборки.
Например, если объем исследуемой совокупности n = 20, то номер медианы
Тогда медианой будет среднее из двух значений признака, стоящих в упорядоченном ряду под номерами 10 и 11:
Размах вариации ‑ разность между максимальным и минимальным значениями признака в совокупности:
Среднее линейное отклонение: Среднее квадратическое отклонение ( Формула расчета следующая: Квадрат среднего квадратического отклонения называется дисперсией ( Она вычисляется по формуле
:
Аналогично рассчитаем показатели для выборок yи z:
Найдем среднее значение по У:
Мода по У:
Медиана по У:
Размах вариации ‑ разность между максимальным и минимальным значениями признака в совокупности:
Среднее линейное отклонение по У:
Среднее квадратическое отклонение по У:
Дисперсия по У:
Коэффициент вариации:
Расчет показателей вариации. Табл.3
Найдем среднее значение по Z:
Медиана по Z:
Размах вариации
Среднее квадратическое отклонение по Z:
Дисперсия по Z:
Среднее линейное отклонение по Z:
Коэффициент вариации:
Расчет показателей вариации. Табл.4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.57.25 (0.007 с.) |

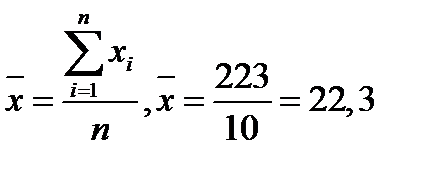

 .
.





 ) представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней.
) представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней.
 ). Дисперсию используют не только для оценки вариации, но и при измерении взаимосвязей, для проверки статистических гипотез.
). Дисперсию используют не только для оценки вариации, но и при измерении взаимосвязей, для проверки статистических гипотез.

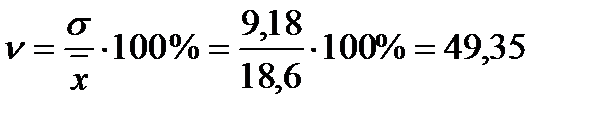

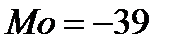







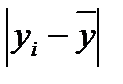













 ,%
,%
 ,%
,%




 ,%
,%
 ,%
,%


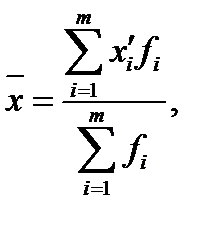



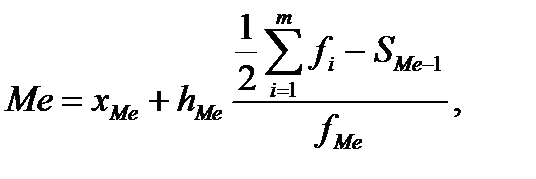

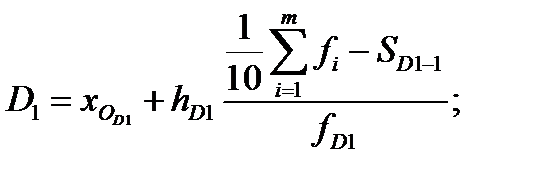
 где
где  ,
,  ‑ начала интервалов, где находятся первая и девятая децили;
‑ начала интервалов, где находятся первая и девятая децили;  ,
,  ‑ величины интервалов, где находятся первая и девятая децили;
‑ величины интервалов, где находятся первая и девятая децили;  ‑ общая сумма частот (частостей);
‑ общая сумма частот (частостей);  ,
,  ‑ суммы накопленных частот (частостей) интервалов, предшествующих тем, в которых находятся первая и девятая децили;
‑ суммы накопленных частот (частостей) интервалов, предшествующих тем, в которых находятся первая и девятая децили;  ,
,  ‑ частоты (частости) интервалов, содержащих первую и девятую децили.
‑ частоты (частости) интервалов, содержащих первую и девятую децили.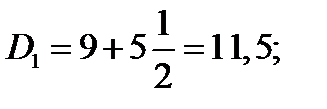
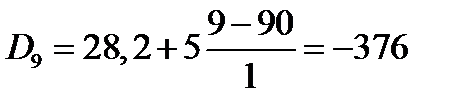
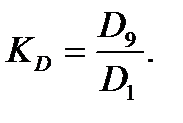





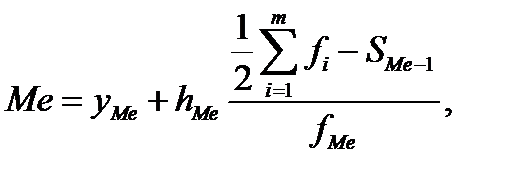






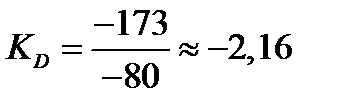


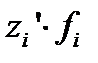




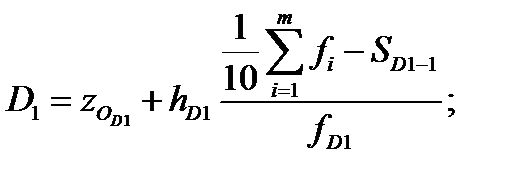

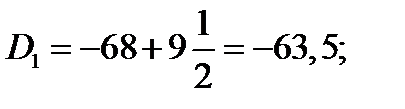

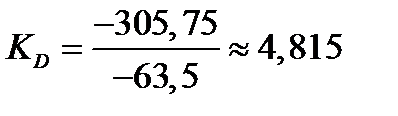
 .
.


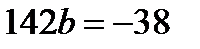 ;
;  ;
; 



 ;
; 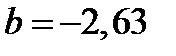 ;
; 



 ;
;  ;
; 
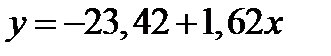
 ,
,  и
и 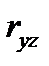 . Сделайте вывод о тесноте линейной связи между признаками.
. Сделайте вывод о тесноте линейной связи между признаками.



 < 0,3 связь считается слабой, при 0,3 <
< 0,3 связь считается слабой, при 0,3 < 

 о равенстве генерального коэффициента корреляции нулю подтверждается с уровнем значимости 5 %. Аналогично
о равенстве генерального коэффициента корреляции нулю подтверждается с уровнем значимости 5 %. Аналогично  .
.



