Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 6. Построение уравнения регрессииСодержание книги
Поиск на нашем сайте
Постройте уравнения регрессии Y(X), Z(X), Z(X) графическим способом. Y(X): Решение: Линия регрессии представлена на графиках в Задании 5. На линии регрессии выбираем две точки, ближе к краям диапазона значений. Уравнение регрессии имеет вид
Составляем систему уравнений ‑ два уравнения с двумя неизвестными:
Уравнение регрессии
Z(X):
Уравнение регрессии
Z(Y):
Уравнение регрессии
Корреляции
Вычислите линейные коэффициенты корреляции Решение:
Вычислим коэффициент rxy:
Вычислим коэффициент rxz:
Вычислим коэффициент ryz:
При
Задача 8. Проверка существенности коэффициентов Корреляции После определения коэффициентов корреляции Решение:
Величина t -критерия имеет вид
где r – выборочный коэффициент корреляции; n – объем выборки.
Проверим существенность коэффициента корреляции rxy:
0,408<2,306, значит гипотеза
11,28>2,306, значит гипотеза
Задача 9. Вычисление параметров Теоретического уравнения регрессии С помощью метода наименьших квадратов (МНК) постройте уравнения регрессии Y(X), Z(Y), Z(X). Нанесите линии регрессии на корреляционное поле. Решение:
Преобразуя полученные уравнения, получаем систему нормальных уравнений МНК для прямой:
Решая систему, получаем оценки неизвестных коэффициентов a и b:
1) Найдем уравнение регрессии Y(x):
Отсюда, линейное уравнение парной регрессии и имеет следующий вид:
2) Найдем уравнение регрессии Z(x):
Отсюда, линейное уравнение парной регрессии и имеет следующий вид:
3) Найдем уравнение регрессии Z(y):
Отсюда, линейное уравнение парной регрессии и имеет следующий вид:
Задача 10. Нахождение средней и предельной ошибки выборки Найдите среднюю и предельную ошибки выборки X, Y, Z. Постройте доверительные интервалы для генеральной средней с вероятностью р = 90 %; 95 %; 99,7 %. Решение: Рассчитаем по Х: Разница между выборочным средним и генеральным средним называется предельной ошибкой выборки:
Составим вспомогательную таблицу: Табл.16
Найдем выборочную среднюю:
Найдем дисперсию:
Определим среднюю ошибку выборки (μ):
Коэффициент доверия t определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности:
1) р = 90 %:
2) р = 95 %:
3) р = 99,7 %:
Рассчитаем по У:
Ход решения такой же, как и при расчетах по Х.
Y: Табл.17
1)р = 90 %:
2)р = 95 %:
3)р = 99,7 %:
Рассчитаем по Z:
Ход решения такой же, как и при расчетах по Х.
Z: Табл.18
1)р = 90 %:
2)р = 95 %:
3)р = 99,7 %:
Задача 11. Сглаживание ряда динамики Решение: 3-членная скользящая средняя простая находится по формуле:
4-членная скользящая средняя простая находится по формуле:
5-членная скользящая средняя взвешенная находится по формуле:
Взвешенная скользящая средняя определяется как средняя арифметическая взвешенная:
где
Веса для уровней ряда при сглаживании могут быть взяты как коэффициенты бинома Ньютона:
Результаты запишем в таблицу:
Табл.19
Нецентрированные скользящие средние:
Центрированные средние:
Табл.20
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.16.251 (0.007 с.) |

 .
.


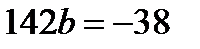 ;
;  ;
; 



 ;
; 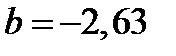 ;
; 



 ;
;  ;
; 
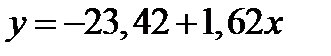
 ,
,  и
и 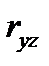 . Сделайте вывод о тесноте линейной связи между признаками.
. Сделайте вывод о тесноте линейной связи между признаками.



 < 0,3 связь считается слабой, при 0,3 <
< 0,3 связь считается слабой, при 0,3 < 

 о равенстве генерального коэффициента корреляции нулю подтверждается с уровнем значимости 5 %. Аналогично
о равенстве генерального коэффициента корреляции нулю подтверждается с уровнем значимости 5 %. Аналогично  .
.




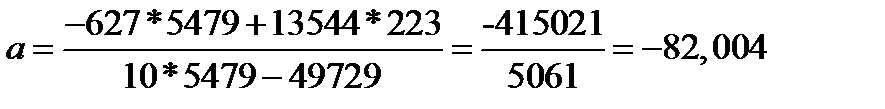
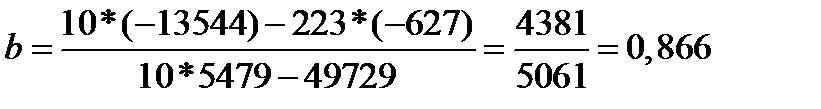
 ,
, 


 ,
, 


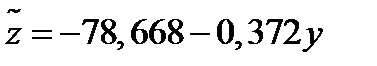







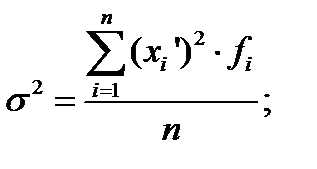
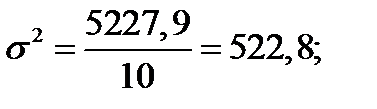

 где
где  ‑ дисперсия
‑ дисперсия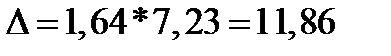








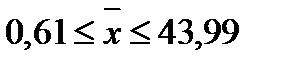





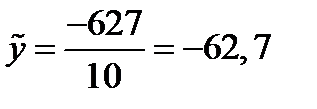

















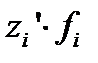



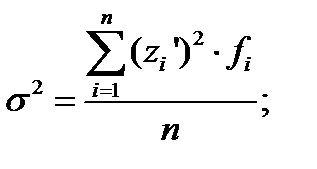


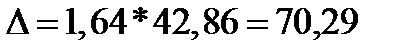

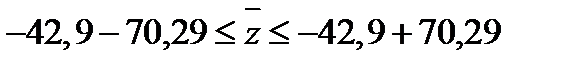
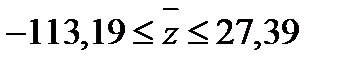



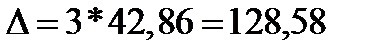

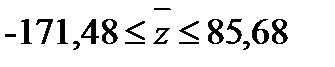

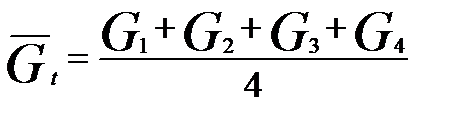
 ,
,
 ‑ скользящая средняя; yt ‑ уровни динамического ряда, участвующие в расчете за интервал n; fi ‑ веса.
‑ скользящая средняя; yt ‑ уровни динамического ряда, участвующие в расчете за интервал n; fi ‑ веса.

 ;
;  ; и т.д.
; и т.д. ;
; 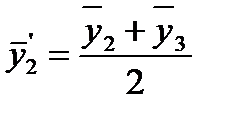 и т.д.
и т.д.