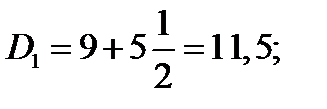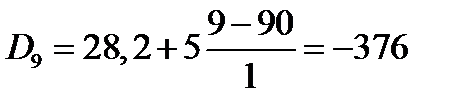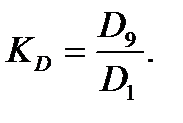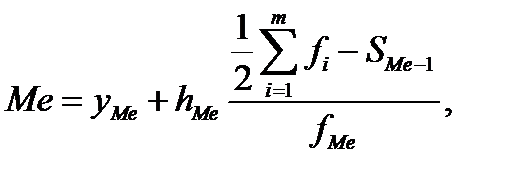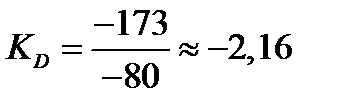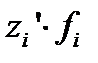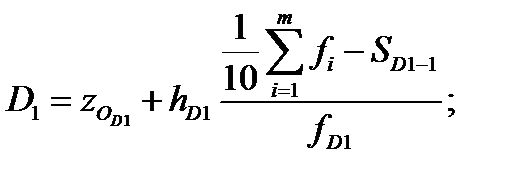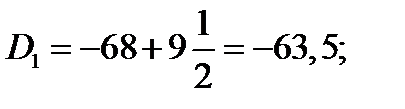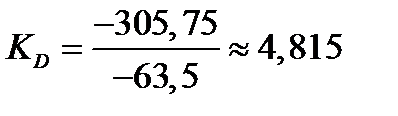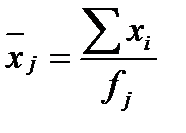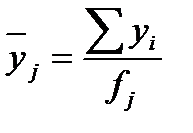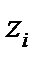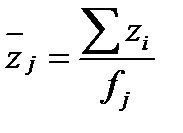Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 2. Построение ряда распределенияСодержание книги
Поиск на нашем сайте
По каждой из выборок X, Y, Z: • проведите группировку данных по интервалам равной длины; • составьте вариационный ряд; • вычислите абсолютные, относительные и накопленные частоты; постройте полигон, гистограмму и кумуляту.
Решение:
Группировка данных и построение вариационного ряда. Табл.5
Рассчитаем по у: Ход решения аналогичный расчетам по Х.
Группировка данных и построение вариационного ряда.
Табл.6
Рис.5 Полигон распределения частот по выборке Y
Рассчитаем по z:
Ход решения аналогичный расчетам по Х.
Группировка данных и построение вариационного ряда. Табл.7
Задача 3. Расчет параметров ряда распределения По сгруппированным данным и графикам определите: · среднее арифметическое; · моду; · медиану; · первую и девятую децили; · коэффициент децильной дифференциации.
Решение: Среднее значение ‑ средняя арифметическая взвешенная:
Расчет среднего значения. Табл.8
Номер медианы нам известен из Задания 1. NMe = 5,5 Точное значение медианы для сгруппированных данных рассчитываем по формуле
где xMe ‑ нижняя граница медианного интервала; h – величина медианного интервала; SMe –1 ‑ накопленная частота (частость) предмедианного интервала, fMe ‑ частота (частость) медианного интервала.
Первая и девятая децили находятся по формулам:
Коэффициент децильной дифференциации находится по формуле (KD):
Рассчитаем по У:
Ход решения аналогичен, как при расчетах по Х.
Расчет среднего значения. Табл.9
Найдем медиану для у:
Найдем первую и девятую децили по у:
Коэффициент децильной дифференциации
Рассчитаем по Z:
Ход решения аналогичен, как при расчетах по Х.
Расчет среднего значения. Табл.10
Значение моды по сгруппированным данным также можно определить по формуле
Найдем медиану для z:
Найдем первую и девятую децили по z:
Коэффициент децильной дифференциации
Задача 4. Аналитическая группировка
Проведите аналитическую группировку Y и Z, используя X и Y как факторные признаки, для выявления зависимостей Y(X), Z (X), Z (Y). Сделайте выводы.
Решение: Вспомогательная таблица для аналитической группировки. Табл.11
Аналитическая группировка.
Вспомогательная таблица для аналитической группировки. Табл.12
Аналитическая группировка. Табл.13
Вспомогательная таблица для аналитической группировки. Табл.14
Аналитическая группировка. Табл.13
Задача 5. Построение корреляционного поля Постройте корреляционное поле. Нанесите линию эмпирической регрессии на корреляционное поле. Сделайте выводы. Решение: Зависимость между признаками проявляется сильнее при нанесении линии эмпирической регрессии, построенной по сгруппированным данным. Для этого необходимо использовать данные аналитической группировки из Задания 4.
9 11,4 13,8 16,2 18,6 21 23,4 25,8 28,2 30,6 33 X
Y Рис. 10 Поле корреляции и эмпирическая линия регрессии
Z Рис. 11 Поле корреляции и эмпирическая линия регрессии
-77,5 -66,5 -55,5 -44,5
Z Рис. 12 Поле корреляции и эмпирическая линия регрессии
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.75.247 (0.009 с.) |



 ,%
,%
 ,%
,%




 ,%
,%
 ,%
,%


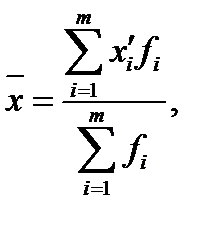



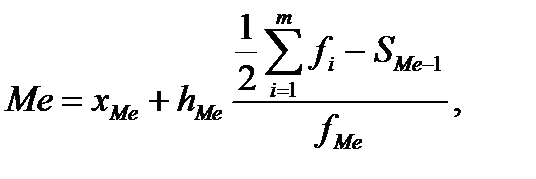

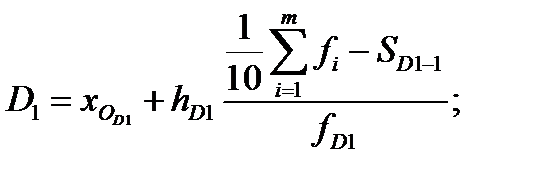
 где
где  ,
,  ‑ начала интервалов, где находятся первая и девятая децили;
‑ начала интервалов, где находятся первая и девятая децили;  ,
,  ‑ величины интервалов, где находятся первая и девятая децили;
‑ величины интервалов, где находятся первая и девятая децили;  ‑ общая сумма частот (частостей);
‑ общая сумма частот (частостей);  ,
,  ‑ суммы накопленных частот (частостей) интервалов, предшествующих тем, в которых находятся первая и девятая децили;
‑ суммы накопленных частот (частостей) интервалов, предшествующих тем, в которых находятся первая и девятая децили;  ,
,  ‑ частоты (частости) интервалов, содержащих первую и девятую децили.
‑ частоты (частости) интервалов, содержащих первую и девятую децили.