
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение напряжений в грунте по подошве жестких фундаментовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если нагрузка передается на грунт жестким фундаментом, то при симметричном загружении осадка поверхности грунта под ним будет равномерной. Это повлечет за собой неравномерное распределение давления по подошве фундамента, обусловливаемое неравномерностью деформации поверхности грунта вокруг фундамента. Теоретическое решение этой задачи для абсолютно жесткого круглого штампа, выполненное Буссинеском, приводит к выражению рρ=рm/(2√(1-ρ2/r2)) рρ – давление по подошве круглого фундамента на расстоянии ρ от его центра при ρ<r r – радиус подошвы фундамента рm – среднее давление по подошве фундамента
57. Предельное напряжение состояний массива грунта. Фазы работы грунтового основания. Предельное напряженное состоянием массива грунта, такое при котором малейшее добавочное силовое воздействие или малейшее уменьшение прочности грунта может привести к нарушению существующего равновесия – к потере устойчивости массива: возникновению в нем поверхности скольжения, развитию различных сдвиговых деформаций и нарушению природной структуры. Обычно нарушение равновесия приводит к выпору грунта из под фундамента, что сопровождается большой осадкой. Т.к. это не допустимо для большинства сооружений важно правильно определить максимальную возможную нагрузку на грунтовое основание. Различают 3 фазы работы грунтового основания:
1 фаза. Осадки пропорциональны давлению сдвиговых деформаций в массиве. Эта фаза ограничивается Рнк (рассматривается по 2 группе предельных состояний по деформациям) 2 фаза. Фаза сдвигов – в массиве в отдельных точках появляются сдвиговые (пластические) деформации, которые с увеличением нагрузки растут а в конце фазы определяемом конечным критическим давлением – Ркк сдвиговые деформации сливаются, образуя поверхности скольжения в этот момент начинается потеря устойчивости всего массива. 3 фаза. Фаза сплошных сдвигов – характеризуется наличием сплошных поверхностей скольжения – полная потеря устойчивости основания (расчет по 1 группе предельных состояний на прочность занимается определением Ркк для данного массива).
58. Определение начального критического давления. Условия равновесия внутри массива под нагрузкой. Sinφ=(σ1-σ3)/(σ1+σ3+2C*ctgφ) Выражения для главных напряжений в любой точке любого сечения массива: σ1=Р(α+sinα)/π; σ2=Р(α-sinα)/π При zmax=0 (zmax – максимальная глубина границы области предельного равновесия), т.е. при отсутствии зон предельного равновесия, получаем теоретическое значение начального критического давления Рн.к. Рн.к.= (π(γ*h+с* ctgφ)/ ctgφ+φ-π/2)+γ*h-формула Пузыревского
59. Определение конечного критического давления.
При работе фундамента во II и III фазах возможно опрокидывание фундамента из-за появления сплошных поверхностей скольжения. При этом будет происходить сдвиг слоев грунта по плоскостям скольжения и выпор грунта на поверхность:
На основании опытных данных К.Терцаги предложил схему деформируемого грунта и на ее основе получил формулу: Рк.к. = Nγγb1 + Nqq+ Ncc Где, Nγ;Nq;Nc - коэффициенты, зависящие от φ и определяются по таблицам; b1 - полуширина фундамента; q= γН - боковая пригрузка; С -удельное сцепление. Наиболее полное решение получено в 1952 году В.В.Соколовским для случая плоской задачи при. действии на поверхности нагрузки, наклоненной под углом б к вертикали, изменяющейся по закону трапеции:
Рк.к = Аγх + Bq+ Сс где, А, В, С - коэффициенты зависящие от φ и
60. Расчет осадок оснований
Различают два вида осадок: 1. Конечная осадка - осадка, рассчитываемая на основе модели линейно-деформируемого полупространства, когда все давление воспринимается скелетом грунта. 2. Осадка во времени - осадка, рассчитываемая на основе теории фильтрационной консолидации (уплотнения) Расчет конечных осадок. Существует выражения для определения относительной вертикальной деформации при трехосном напряженном состоянии (теория упругости): Единичный обьем:
Деформации единичного объема: εz=[σz-μ(σx-σy)]/E Для вычисления осадки полупространства необходимо проинтегрировать последнее выражение S=(Интеграл от 0 до ∞) εz dz В случае сосредоточенной силы, приложенной к полупространству:
SA=P(1-μ2)/πEr
где, Р - сосредоточенная сила;Е - модуль деформации; μ- коэффициент Пуассона; r – расстояние от точки А до места приложения нагрузки В случае равномерно распределенной нагрузки пользуются методом перехода к элементарным сосредоточенным силам и интегрированию по всех площади загружения. В результате получают формулу для определения осадки полупространства:
S=qbω(1-μ2)/E где, q - распределенная нагрузка; ω- коэффициент, зависящий от формы загруженной площади и местоположения точки. Для жесткого штампа наше решение принимает вид формулы Шлейхера: E0=ω(1-μ02)Pb/S S=Pbω(1-μ02)/E0 p- давление на подошву фундамента b- диаметр или сторона фундамента; E0-модуль деформации грунта; Этой формулой можно пользоваться для определения осадки основания фундамента в ограниченных случаях.
61. Метод расчета осадок оснований по СНиП В СНиПе предусмотрен другой метод расчета осадок оснований. Он основан на схеме работы грунта при невозможности бокового расширения. Это дает возможность выразить напряжения по осям X и Y через σz σx=σy=μσz/(1-μ) Тогда выражение для вычисления деформаций единичного обьема грунта основания примет вид: εz=(1-[2μ0/(1-μ0)])σz/E0, где β=(1-2μ02)/(1-μ0)=0,8 согласно СНиП для всех грунтов Задача расчета осадки основания сводиться к вычислению интеграла. СНиП предусматривает вычисление интеграла численным методом путем разбиения грунтовой толщи основания на отдельные элементарные слои толциной hi и при этом вводятся следующие допущения: 1. Каждый элементарный слой имеет постоянные Е0 и μ0 2. Напряжение в элементарном слое постоянно по глубине и равно полусумме верхнего и нижнего напряжений 3. Имеется граница сжмаемой толщи на глубине, где σzp=0.2σzq (где σzq напряжение от собственного веса грунта)
62. Алгоритм расчета осадки основания фундамента 1. Основание разбивается на элементарные слои толщиной; где hi<0.4b, b- ширина подошвы фундамента. 2. Строиться эпюра нарпяжений от собственного веса грунта σzq 3. Строиться эпюра напряжений от внешней нагрузки σzp 4. Устанавливается граница сжимаемой толщи. 5. Определяетсяя напряжение в каждом элементарном слое:
σzpi=(σzpверх +σzpниж)/2
6. Рассчитывается осадка каждого элементарного слоя: Si=βσzpihi/Ei
7. Вычисляется конечная осадка основания фундамента, как сумма осадок
При наблюдении за осадками оснований фундаментов был получен график развития осадок во времени. Вводиться понятие степени консолидации: U=St/SKOH Конечная осадка рассчитывается методом СНиП. Степень консолидации определяется решением дифференциального уравнения одномерной фильтрации: U=1-16(1-2/π)e-N/π2+(1+2/(3π))e-9N/9+… Физический смысл степени консолидации выражает величина показателя N: N=π2kФt/(4m0h2γω)
Где, kФ ~ коэффициент фильтрации, [см/год] m0 – коэффициент относительной сжимаемости слоя; [см2/кг] h - толщина сжимаемого слоя; [см] t - время; [год] γω - удельный вес воды
Устойчивость откосов Откосом называется искусственно созданная наклонная поверхность, ограничивающая естественный грунтовый массив или насыпь. Устойчивость откосов зависит от: - прочности грунтов под откосом и в его основании, причем характеристики прочности могут изменяться со временем; - удельного веса грунтов под откосом и в его основании; - крутизны откоса; - высоты откоса; - нагрузок на поверхности откоса; - фильтрации воды через откос; - положения уровня воды, насыщающей грунт в теле откоса. Разрушение откоса может происходить внезапно и носить характер обвала или оплыва, а также проявляться в виде длительного оползания, что особенно характерно для глинистых грунтов. В ряде случаев грунты оснований под откосом являются менее прочными, чем грунты в теле откоса. Тогда становится возможным их выдавливание из-под откоса, с обрушением всего откоса или его части. Предельно устойчивым называется откос, под которым в каждой точке грунт находится в предельно напряженном состоянии. Теоретически предельно устойчивый откос из сыпучего грунта - песка имеет прямолинейный контур с углом наклона к горизонту, равным углу внутреннего трения.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.93.183 (0.008 с.) |









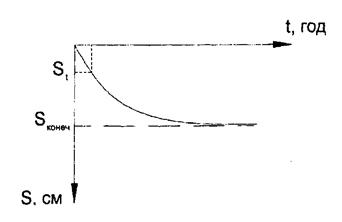 64. Понятие о расчете осадок во времени
64. Понятие о расчете осадок во времени


